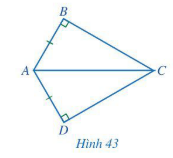
Cho Hình 43 có AB = AD, góc ABC = góc ADC = 90°. Chứng minh góc ACB = góc ACD

Bài 2 trang 83 Toán 7 Tập 2:

Cho Hình 43 có AB = AD, $\widehat{ABC}=\widehat{ADC}=90°.$ Chứng minh $\widehat{ACB}=\widehat{ACD}.$ 

Trả lời

Chứng minh (Hình 43):

Vì $∆$ABC có $\widehat{ABC}=90°$ (giả thiết) nên $∆$ABC vuông tại B.

Vì ∆ADC có $\widehat{ADC}=90°$ (giả thiết) nên ∆ADC vuông tại D.

Xét hai tam giác ABC (vuông tại B) và tam giác ADC (vuông tại D) có:

AC là cạnh chung

AB = AD (giả thiết)

Suy ra $∆$ABC = ∆ADC (cạnh huyền – cạnh góc vuông)

Do đó $\widehat{ACB}=\widehat{ACD}$ (hai góc tương ứng)

Vậy $\widehat{ACB}=\widehat{ACD}$

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 3: Hai tam giác bằng nhau

Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân