Cho hàm số y=f(x)có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình 1+f(x^3-3x^2+1)≥√(2f^2 (x^3-3x^2+1)+2) là
Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình
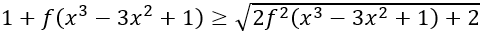 là
làA. 5
B. 4
C. 3
D. 2
Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình
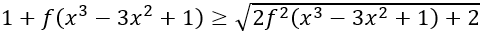 là
làA. 5
B. 4
C. 3
D. 2
Chọn A
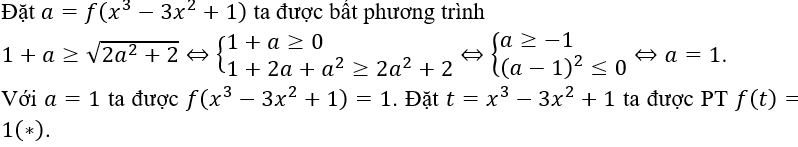
Vẽ đường thẳng y=1 lên đồ thị đã cho ta được PT (*)có 1 nghiệm và 1 nghiệm .
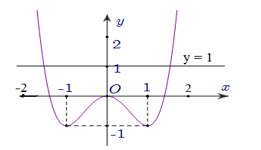
Ta có BBT của hàm số như sau
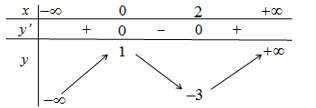
Với ta được PT . Dựa vào BBT ta thấy PT này có 3 nghiệm phân biệt.
Với ta được PT . Dựa vào BBT ta thấy PT này có 1 nghiệm.
Vậy BPT đã cho có 4 nghiệm thực.