Cho hàm số y=f(x) có đồ thị y=f'(x) như hình bên dưới Số điểm cực trị của hàm số g(x)=f(x^3+3x^2)+2020 là
Cho hàm số có đồ thị như hình bên dưới
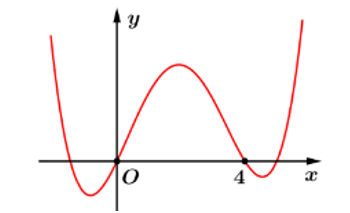
Số điểm cực trị của hàm số là
A. 6
B. 5
C. 4
D. 3
Cho hàm số có đồ thị như hình bên dưới

Số điểm cực trị của hàm số là
A. 6
B. 5
C. 4
D. 3
Chọn A
Ta có .
.
Ta có .
Ta có .
Xét hàm số , có .
Bảng biến thiên của hàm :
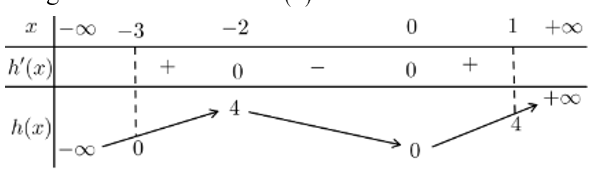
Dựa vào bảng biến thiên của hàm , ta có:
Phương trình có duy nhất một nghiệm (nghiệm đơn) .
Phương trình có duy nhất một nghiệm (nghiệm đơn) .
Do đó, phương trình có 4 nghiệm đơn phân biệt là và 2 nghiệm bội 3 là nên hàm số có 6 điểm cực trị.