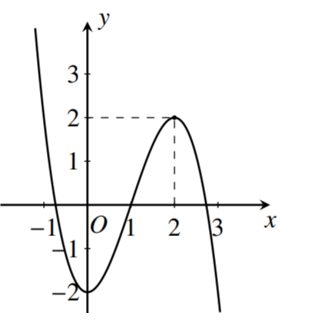
Cho hàm số y=f(x)  có đạo hàm trên R. Biết rằng hàm số y=f(x) có đồ thị như hình bên. Đặt g(x)=f(f(x)). Hỏi hàm số g(x) có bao nhiêu điểm cực trị?

Cho hàm số y=f(x)  có đạo hàm trên R. Biết rằng hàm số y=f(x) có đồ thị như hình bên. Đặt $g\left(x\right)=f\left(f\left(x\right)\right)$. Hỏi hàm số g(x) có bao nhiêu điểm cực trị?

A. 4

B. 5

C. 7

D. 6

Trả lời

Chọn D

Ta có $g^{\text{'}}\left(x\right)=f^{\text{'}}\left(x\right).f^{\text{'}}\left(f\left(x\right)\right)$

$\Rightarrow g^{\text{'}}\left(x\right)=0\iff \left[\begin{array}{l}{f}^{\text{'}}\left(x\right)=0\\ f^{\text{'}}\left(f\left(x\right)\right)=0\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=2\\ f\left(x\right)=0\\ f\left(x\right)=2\end{array}\right.$

Số cực trị của hàm số $g\left(x\right)$ là số nghiệm đơn của phương trình $g^{\text{'}}\left(x\right)=0$

Dựa vào đồ thị ta thấy $f\left(x\right)=0$ có 3 nghiệm đơn phân biệt, $f\left(x\right)=2$ có 1 nghiệm đơn và 1 nghiệm kép.

Nên $g^{\text{'}}\left(x\right)=0$ có 6 nghiệm đơn phân biệt.

Vậy hàm số g(x) có 6 điểm cực trị.