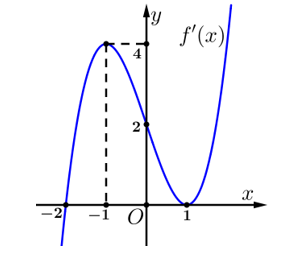
Cho hàm số y=f(x) có đạo hàm liên tục trên R và hàm số $y=f^{\text{'}}\left(x\right)$  có đồ thị như hình vẽ sau:

Số điểm cực trị của hàm số $y=f\left(x-2017\right)-2018x+2019$   là:.

Chọn D

Đặt $g\left(x\right)=f\left(x-2017\right)-2018x+2019$ .

Ta có: $g\text{'}\left(x\right)=f\text{'}\left(x-2017\right)-2018$ .

Đồ thị hàm số $y=f\text{'}\left(x-2017\right)$  là phép tịnh tiến đồ thị hàm số $y=f\text{'}\left(x\right)$  theo phương trục hoành sang phải 2017  đơn vị.

Đồ thị hàm số $y=f\text{'}\left(x-2017\right)$  cắt đường thẳng y=2018  tại duy nhất  một điểm có hoành độ $x_0>1$  và giá trị hàm số $g\text{'}\left(x\right)$  đổi dấu từ âm sang dương khi qua điểm $x_0$  nên hàm số đạt cực tiểu tại $x_0$ ,