Cho hàm số y= f(x) liên tục trên R và có đạo hàm là f'(x)= ( x-20^2( x^2-4x+3) . Hàm số f(x) có bao nhiêu điểm cực tiểu?

A. 0

B. 2

C. 1

D. 3

Trả lời

$f^{\text{'}}\left(x\right)={\left(x-2\right)}^2\left(x^2-4x+3\right)$

Ta có: $f^{\text{'}}\left(x\right)=0\iff \left[\begin{array}{l}x=2\\ x=1\\ x=3\end{array}\right.$

Ta có bảng xét dấu  như sau :

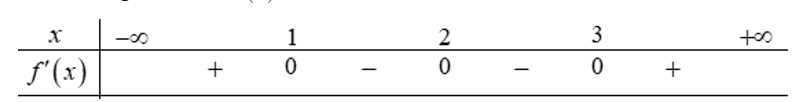
Theo bảng xét dấu trên ta suy ra hàm số có một điểm cực tiểu là $x=3$.