Cho hàm số y = f( x ) có đồ thị trên [ - 2;6] như hình vẽ bên. Biết các miền A, B, x = 2 có diện tích lần lượt là 32; 2; 3. Tích phân limits - 2^2 [ f( 2x + 2) + 1]dx bằng A. 45/2. B. 41.
38
19/04/2024
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên \(\left[ { - 2;6} \right]\) như hình vẽ bên. Biết các miền A, B, \(x = 2\) có diện tích lần lượt là 32; 2; 3.
Tích phân \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} \) bằng
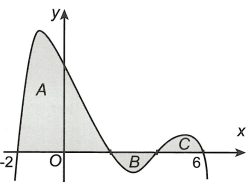
A. \(\frac{{45}}{2}\).
B. 41.
C. 37.
D. \(\frac{{41}}{2}\).
Trả lời
Hướng dẫn giải
Ta có \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} = \int\limits_{ - 2}^2 {f\left( {2x + 2} \right)dx} + 4\)
Xét \({I_1} = \int\limits_{ - 2}^2 {f\left( {2x + 2} \right)dx} \).
Đặt \(t = 2x + 2 \Rightarrow dt = 2dx \Rightarrow dx = \frac{{dt}}{2}\)
Đổi cận: \(x = - 2 \Rightarrow t = - 2\); \(x = 2 \Rightarrow t = 6\).
Suy ra \({I_1} = \frac{1}{2}\int\limits_{ - 2}^6 {f\left( t \right)dt} \).
Gọi \({x_1}\); \({x_2}\) là các hoành độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trực hoành \[\left( { - 2 < {x_1} < {x_2} < 6} \right)\] . Ta có
\[\begin{array}{l}{I_1} = \frac{1}{2}\left( {\int\limits_{ - 2}^{{x_1}} {f\left( t \right)df} + \int\limits_{{x_1}}^{{x_2}} {f\left( t \right)df} + \int\limits_{{x_2}}^6 {f\left( t \right)df} } \right) = \frac{1}{2}\left( {{S_A} - {S_B} + {S_C}} \right)\\ = \frac{1}{2}\left( {32 - 2 + 3} \right) = \frac{{33}}{2}\end{array}\]
Vậy \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} = {I_1} + 4 = \frac{{33}}{2} + 4 = \frac{{41}}{2}\)
Chọn D.

