Cho hàm số y = f( x )có đạo hàm trên R và có đồ thị như hình vẽ sau: Số cực trị của hàm số y = f( x )^2 là A. 5 B. 3 C. 1 D. 4
39
25/04/2024
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\)và có đồ thị như hình vẽ sau:
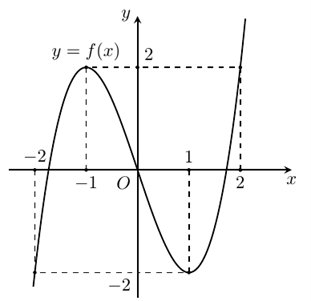
Số cực trị của hàm số \(y = {\left[ {f\left( x \right)} \right]^2}\) là
A. \(5\).
B. \(3\).
C. \(1\).
D. \(4\).
Trả lời
Lời giải
Chọn A
Ta có: \(y' = 2f\left( x \right)f'\left( x \right)\).
\(y' = 0 \Leftrightarrow 2f\left( x \right)f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f'\left( x \right) = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\,\,\left( {a \in \left( { - 2;\, - 1} \right)} \right)\\x = 0\\x = b\,\,\left( {b \in \left( {1;\,2} \right)} \right)\\x = - 1\\x = 1\end{array} \right.\)
Bảng biến thiên
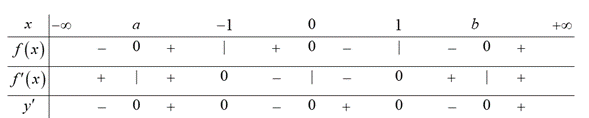
Dựa vào bảng biến thiên ta thấy đạo hàm đổi dấu 5 lần. Do đó, hàm số đã cho có 5 cực trị


