Cho hàm số y = f( x ) có đạo hàm f'( x ) trên và đồ thị của hàm số f'( x ) như hình vẽ. Tìm số điểm cực trụ hàm số g( x ) = f( x^2 - 2x - 1). A. 3 B. 5 C. 4 D. 6
44
04/05/2024
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) trên 
và đồ thị của hàm số \(f'\left( x \right)\) như hình vẽ.
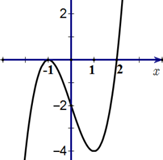
Tìm số điểm cực trụ hàm số \(g\left( x \right) = f\left( {{x^2} - 2x - 1} \right)\).
A. \(3\).
B. \(5\).
C. \(4\).
D. \(\;6\).
Trả lời
Lời giải
Chọn A
Ta có: \(g'\left( x \right) = \left( {2x - 2} \right)f'\left( {{x^2} - 2x - 1} \right)\). Nhận xét: \(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{{x^2} - 2x - 1 = - 1}\\{{x^2} - 2x - 1 = 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \pm 1}\\{x = 2;x = 3}\end{array}} \right.\)
Ta có bảng biến thiên:
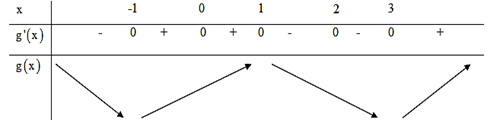
Dựa vào bảng biến thiên, ta thấy hàm số có đúng ba cực trị.
