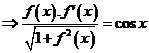Cho hàm số f(x) liên tục, không âm trên đoạn đoạn (0; pi/2), thỏa mãn f(0)= căn 3
Cho hàm số f(x) liên tục, không âm trên đoạn , thỏa mãn và , . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f(x) trên đoạn .
A. , .
B. , .
C. , .
D. , .
Chọn A
Từ giả thiết
Đặt .
Thay vào ta được .
Do .
Vậy
, vì hàm số f(x) liên tục, không âm trên đoạn .
Ta có , xét hàm số có hoành độ đỉnh loại.
Suy ra , .
Suy ra , .
Từ giả thiết
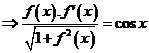
Đặt .
Thay vào ta được .
Do .
Vậy
, vì hàm số f(x) liên tục, không âm trên đoạn .
Ta có , xét hàm số có hoành độ đỉnh loại.
Suy ra , .
Suy ra , .