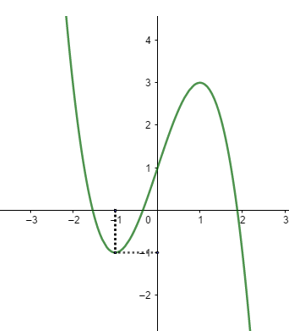
Cho hàm số f(x), hàm số f'(x) liên tục trên R và có đồ thị như hình vẽ. Bất phương trình $f\left(x\right)<x+m$ (m là một số thực) nghiệm đúng với mọi $x\in \left(-1;0\right)$ khi và chỉ khi:

Chọn B

Ta có: $f\left(x\right)<x+m\iff f\left(x\right)-x<mf\left(x\right)<x+m\iff f\left(x\right)-x<m$.

Xét $g\left(x\right)=f\left(x\right)-x$, ta có: $g^{\text{'}}\left(x\right)=f^{\text{'}}\left(x\right)-1$. Với mọi $x\in \left(-1;0\right)$ thì $-1<f^{\text{'}}\left(x\right)<1$.

Từ đó $g^{\text{'}}\left(x\right)=f^{\text{'}}\left(x\right)-1<0$ nên hàm số nghịch biến trên $\left(-1;0\right)$.

Suy ra $g\left(x\right)=f\left(x\right)-x<f\left(-1\right)+1$. Yêu cầu bài toán tương đương với $m\ge f\left(-1\right)+1$.