Cho hàm số f(x) có đạo hàm xác định trên R là $f^{\text{'}}\left(x\right)=x\left(x^2-1\right)\sqrt{x^2+3}$. Giả sử a, b là hai số thực thay đổi sao cho $a<b\le 1$. Giá trị nhỏ nhất của $f\left(a\right)-f\left(b\right)$ bằng

A. $\frac{\sqrt{3}-64}{15}$. 

B. $\frac{33\sqrt{3}-64}{15}$. 

C. $-\frac{\sqrt{3}}{5}$. 

D. $-\frac{11\sqrt{3}}{5}$.

Chọn D

Ta có: $y^{\text{'}}=f^{\text{'}}\left(x\right)=x\left(x^2-1\right)\sqrt{x^2+3}$ suy ra $y=f\left(x\right)=\int x\left(x^2-1\right)\sqrt{x^2+3}\text{d}x$
Đặt $t=\sqrt{x^2+3}\Rightarrow t^2-3=x^2\Rightarrow x\text{d}x=t\text{d}t$
Suy ra
$\int x\left(x^2-1\right)\sqrt{x^2+3}\text{d}x=\int \left(t^2-4\right)t^2\text{d}t=\int \left(t^4-4t^2\right)\text{d}t=\frac{{\displaystyle t^5}}{{\displaystyle 5}}-\frac{{\displaystyle 4}}{{\displaystyle 3}}{t}^3+C$, với C là hằng số.
Từ đó: $f\left(x\right)=\frac{{\left(x^2+3\right)}^2\sqrt{x^2+3}}{5}-\frac{4\left(x^2+3\right)\sqrt{x^2+3}}{3}+C$
Mặt khác $f\text{'}\left(x\right)=0\iff x\left(x^2-1\right)\sqrt{x^2+3}=0\iff \left[\begin{array}{c}x=0\\ x=\pm 1\end{array}\right.$.
Bảng biến thiên

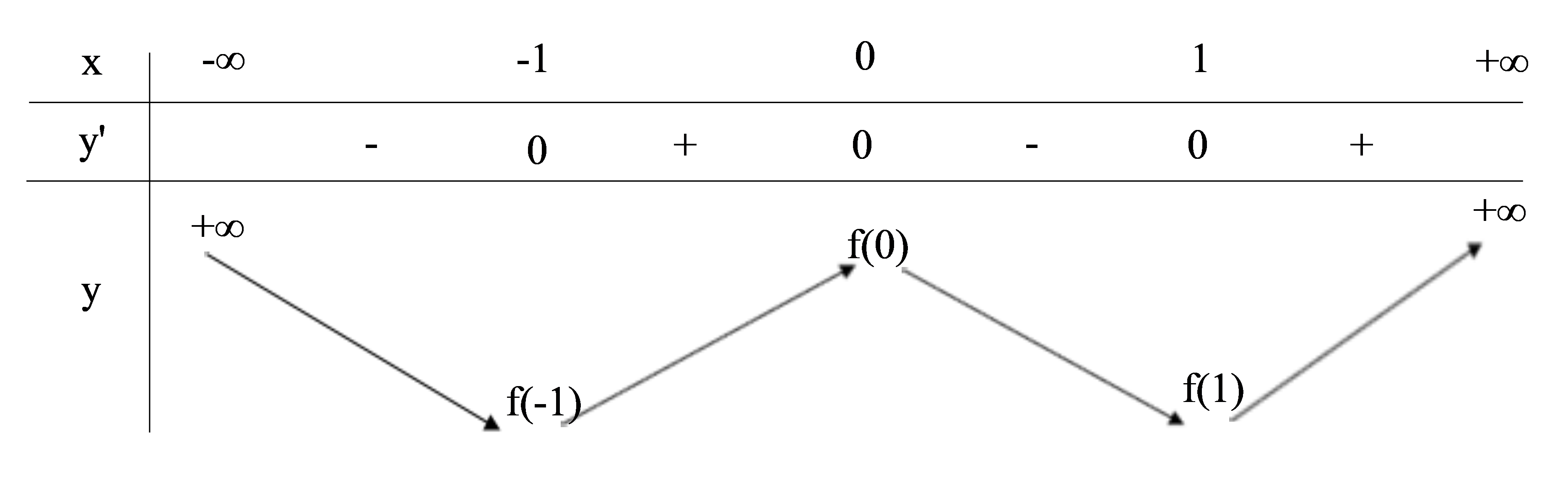
Dựa và bảng biến thiên, ta có nhận xét:
Trên khoảng $\left(-\infty ;-1\right)$ hàm nghịch biến, do đó với $a<b<-1\Rightarrow f\left(a\right)>f\left(b\right)$ nên $f\left(a\right)-f\left(b\right)>0$.
Trên đoạn $\left[-1;1\right]$, để $f\left(a\right)-f\left(b\right)$ đạt GTNN thì f(a) đạt GTNN và f(b) đạt GTLN.
Do đó $\left\{\begin{array}{c}a=-1\\ b=0\end{array}\right.$, vì $a<b\le 1.$
Suy ra giá trị nhỏ nhất của $f\left(a\right)-f\left(b\right)=f\left(-1\right)-f\left(0\right)$.
Vậy $f\left(-1\right)-f\left(0\right)=\left(\frac{16.2}{5}-\frac{16.2}{3}\right)-\left(\frac{9\sqrt{3}}{5}-\frac{12\sqrt{3}}{3}\right)=\frac{33\sqrt{3}-64}{15}$