Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Kẻ 2 tiếp tuyến AM, AN và cát tuyến ABC với đường tròn (AB < AC). Qua O kẻ OK vuông góc với BC tại K, OK cắt MN tại S. Chứng minh SC là tiếp tuyến của đường tròn (O).

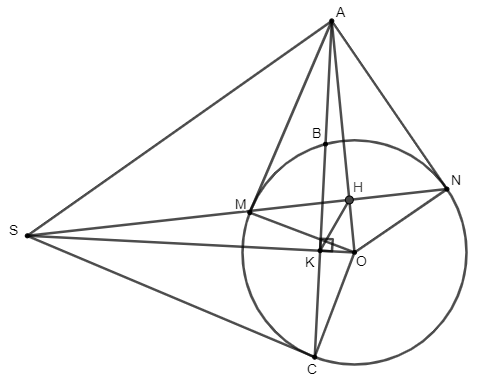
Gọi AO ∩ MN ≡ H

Theo tính chất hai tiếp tuyến cắt nhau: AM = AN

Mà OM = ON nên OA là trung trực của MN

Do đó OA ⊥ MN  $\iff \widehat{SHA}=90°$ (1)

Mặt khác BC ⊥ OK ⟹ AC⊥ OS ⟹  $\widehat{SKA}=90°$ (2)

Từ (1) và (2) suy ra tứ giác SKHA nội tiếp (hai góc cùng nhìn một cạnh bằng nhau)

Do đó theo tính chất tứ giác nội tiếp thì: OK.OS = OH.OA (*)

Vì AM là tiếp tuyến của đường tròn (O) nên AM ⊥ OM

Xét tam giác vuông AMO có đường cao MH, theo hệ thức lượng trong tam giác vuông thì: OC² = R² = OM² = OH.OA (**)

Từ (*) và (**) ⟹ OC² = OK.OS  $\iff \frac{OC}{OK}=\frac{OS}{OC}$

Do đó tam giác OCK đồng dạng với tam giác OSC (cạnh – góc – cạnh)

⇒ SC ⊥ OC ⇒ SC là tiếp tuyến của đường tròn (O).