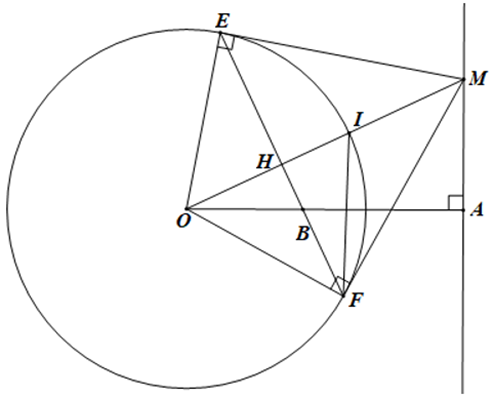
a) Do ME, MF là hai tiếp tuyến của (O) nên ME = MF.

Khi đó M thuộc đường trung trực của đoạn EF       (1)

Lại có OE = OF = R.

Suy ra O thuộc đường trung trực của đoạn EF        (2)

Từ (1), (2), suy ra OM là đường trung trực của đoạn EF.

Do đó OM ⊥ EF.

Ta có \[\widehat {MHB} + \widehat {MAB} = 90^\circ + 90^\circ = 180^\circ \].

Vậy tứ giác ABHM nội tiếp đường tròn đường kính MB.

b) Xét ∆OHB và ∆OAM, có:

\(\widehat {HOB}\) chung;

\(\widehat {OHB} = \widehat {OAM} = 90^\circ \).

Do đó  (g.g).

Suy ra \(\frac{{OH}}{{OA}} = \frac{{OB}}{{OM}}\).

Vì vậy OH.OM = OA.OB         (3)

Tam giác OEM vuông tại E có EH là đường cao:

OE² = OH.OM (Hệ thức lượng trong tam giác vuông).

⇔ R² = OH.OM    (4)

Từ (3), (4), ta thu được OA.OB = OH.OM = R².

c) Gọi I là giao điểm của OM với đường tròn (O).

Ta có \(\widehat {MFI} = \widehat {FEI}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung FI)   (5)

Do EF ⊥ OM nên .

Suy ra \(\widehat {FEI} = \widehat {EFI}\) (hai góc nội tiếp chắn hai cung bằng nhau)   (6)

Từ (5), (6), suy ra \(\widehat {MFI} = \widehat {EFI}\).

Do đó FI là tia phân giác của \(\widehat {MFE}\).

Tam giác MEF cân tại M có MH là đường trung trực.

Suy ra MH cũng là đường phân giác của tam giác MEF.

Ta có I là giao điểm của hai đường phân giác FI, MH của tam giác MEF.

Khi đó I là tâm của đường tròn nội tiếp tam giác MEF.

Mà I thuộc đường tròn (O) cố định.

Vậy ta có điều phải chứng minh.

d) Ta có \({S_{\Delta HBO}} = \frac{1}{2}OH.HB\).

Ta có  (chứng minh trên).

Suy ra \(\frac{{HB}}{{AM}} = \frac{{OB}}{{OM}}\).

Do đó HB.OM = AM.OB         (7)

Lại có OH.OM = R² (kết quả câu b)    (8)

Nhân (7) và (8) vế theo vế, ta được: \(OH.HB.O{M^2} = {R^2}.AM.OB = {R^2}.AM.\frac{{{R^2}}}{{OA}}\).

\( \Rightarrow OH.HB = AM.\frac{{{R^4}}}{{OA.O{M^2}}} = {R^4}.\frac{{AM}}{{OA.\left( {O{A^2} + A{M^2}} \right)}}\).

Áp dụng bất đẳng thức Cauchy, ta được: OA² + AM² ≥ 2OA.AM.

Khi đó ta có \(OH.HB = {R^4}.\frac{{AM}}{{OA.\left( {O{A^2} + A{M^2}} \right)}} \le {R^4}.\frac{{AM}}{{OA.2.OA.AM}} = \frac{{{R^4}}}{{2O{A^2}}}\).

Suy ra \({S_{\Delta HBO}} \le \frac{{{R^4}}}{{4O{A^2}}}\).

Dấu “=” xảy ra ⇔ OA = AM.

Vì vậy diện tích tam giác HBO lớn nhất bằng \(\frac{{{R^4}}}{{4O{A^2}}}\) khi và chỉ khi OA = OM.

Vậy M là điểm nằm trên đường thẳng d sao cho OA = OM thì diện tích tam giác HBO lớn nhất.