Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ đường kính CD. Tia phân giác của \(\widehat {BOD}\) cắt AB tại E.
a) Chứng minh rằng ED là tiếp tuyến của đường tròn (O).
b) Chứng minh AC + DE ≥ 2R.
c) Tính số đo \(\widehat {AOE}\).
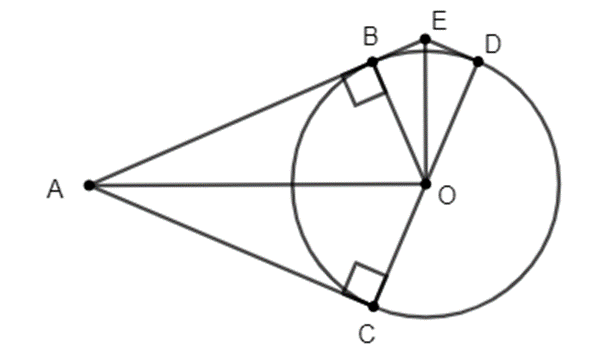
a) Xét ∆OBE và ∆ODE có:
OE là cạnh chung
\(\widehat {BOE} = \widehat {DOE}\) (gt)
OB = OD = R
Do đó ∆OBE = ∆ODE (c.g.c)
Suy ra \(\widehat {OBE} = \widehat {ODE} = 90^\circ \)
Do đó ED là tiếp tuyến của đường tròn (O).
b) Theo tính chất của hai tiếp tuyến cắt hau, ta có:
AC = AB; BE = DE
Nên: AC + DE = AB + BE = AE (1)
Từ câu a) ta có CD\( \bot \)DE, mà CD\( \bot \)AC (gt) nên ED // AC.
Vì CD là khoảng cách giữa hai đường thẳng song song AC và DE
nên AE ≥ CD = 2R (2)
Từ (1) và (2) suy ra: AC + DE ≥ 2R.
c) Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
OA là tia phân giác của \(\widehat {BOC}\), OE là tia phân giác của \(\widehat {BOD}\).
Mà \(\widehat {BOC}\) và \(\widehat {BOD}\) kề bù nên \(\widehat {AOE} = 90^\circ \).