Cho ∆ABC ᔕ ∆MNP. a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ

Bài 5 trang 82 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP.

a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ.

b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh ∆ABG ᔕ ∆MNK.

Trả lời

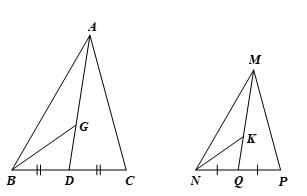
a) Vì ∆ABC ᔕ ∆MNP (giả thiết) nên $\widehat{\mathrm{ABC}}=\widehat{\mathrm{MNP}}$ và $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{BC}}{\mathrm{NP}}$

Vì D, Q lần lượt là trung điểm của BC và NP nên $\mathrm{BD}=\frac{1}{2}\mathrm{BC},\mathrm{NQ}=\frac{1}{2}\mathrm{NP}$

Do đó $\frac{\mathrm{BD}}{\mathrm{NQ}}=\frac{\frac{1}{2}\mathrm{BC}}{\frac{1}{2}\mathrm{NP}}=\frac{\mathrm{BC}}{\mathrm{NQ}},$ suy ra $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{BD}}{\mathrm{NQ}}\left(=\frac{\mathrm{BC}}{\mathrm{NP}}\right)$

Xét ∆ABDvà ∆MNQ có:

$\widehat{\mathrm{ABD}}=\widehat{\mathrm{MNQ}}$ (do $\widehat{\mathrm{ABC}}=\widehat{\mathrm{MNP}});$

$\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{BD}}{\mathrm{NQ}}$

Suy ra ∆ABD ᔕ ∆MNQ (c.g.c).

b) Vì ∆ABD ᔕ ∆MNQ (câu a) $\widehat{\mathrm{BAD}}=\widehat{\mathrm{NMQ}}$ (hai góc tương ứng) và $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{AD}}{\mathrm{MQ}}$ (tỉ số đồng dạng)

Mà G, K lần lượt là trọng tâm của hai tam giác ABC và MNP nên $\mathrm{AG}=\frac{2}{3}\mathrm{AD},\mathrm{MK}=\frac{2}{3}\mathrm{MQ}$

Do đó $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{AD}}{\mathrm{MQ}}=\frac{\frac{2}{3}\mathrm{AD}}{\frac{2}{3}\mathrm{MQ}}=\frac{\mathrm{AG}}{\mathrm{MK}}$

Xét ∆ABG và ∆MNK có:

$\widehat{\mathrm{BAG}}=\widehat{\mathrm{NMK}}$ (do $\widehat{\mathrm{BAD}}=\widehat{\mathrm{NMQ}});$

$\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{AG}}{\mathrm{MK}}$

Vậy ∆ABG ᔕ ∆MNK (c.g.c).

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác: