Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong. Qua I vẽ đường thẳng vuông

Trả lời

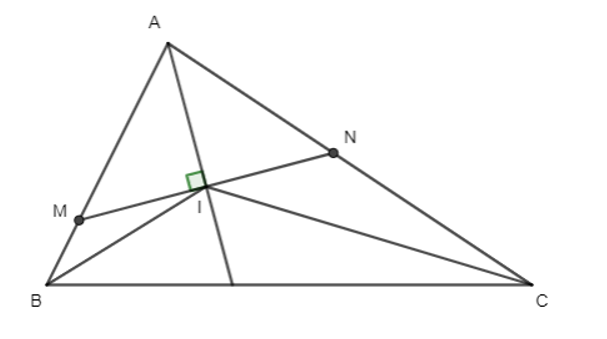
a) Xét tam giác AIM vuông tại I có: $\widehat{AMI}=90°-\frac{1}{2}\widehat{A}=\frac{1}{2}\left(180°-\widehat{A}\right)=\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

$\Rightarrow \widehat{BMI}=180°-\widehat{AMI}=180°-\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

Xét tam giác BIC, có: $\widehat{BIC}=180°-\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

$\Rightarrow \widehat{BMI}=\widehat{BIC}$

Xét ∆BMI và ∆BIC, có:

$\Rightarrow \widehat{BMI}=\widehat{BIC}$ (cmt)

_{$\widehat{MBI}=\widehat{IBC}$}

 ⇒ ∆BMI ̴ ∆BIC (g – g)

$\Rightarrow \frac{BM}{BI}=\frac{BI}{BC}\iff B{I}^2=BM.BC$

Chứng minh tương tự ta có ∆CNI ̴ ∆CIB (g – g)

$\Rightarrow \frac{CN}{CI}=\frac{CI}{CB}\iff C{I}^2=CN.CB$

$\Rightarrow \frac{B{I}^2}{C{I}^2}=\frac{BM}{CN}$.

b) Từ cm trên suy ra :△BMI ∼ △INC

_{$\Rightarrow \frac{BM}{IN}+\frac{MI}{NC}$}

⇒ BM.CN = MI.NI

ta có : △AMN là tam giác cân

⇒ MI = NI

⇒ BM.CN = IM²

ta lại có : △AIM vuông

⇒ IM² = AM² – AI²

⇒ BM.CN = AM² – AI²

= AM.AN – AI² = (AB − BM)(AC − CN) – AI²

= AB.AC − AB.CN − BM.AC + BM.CN – AI²

⇒ BM.AC + CN.AB + AI² = AB.AC.