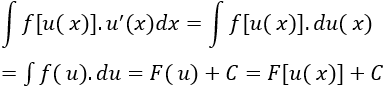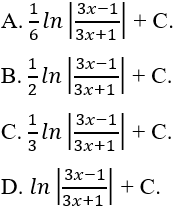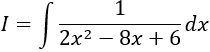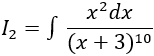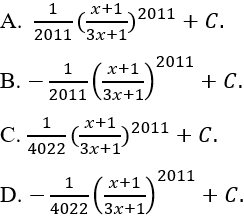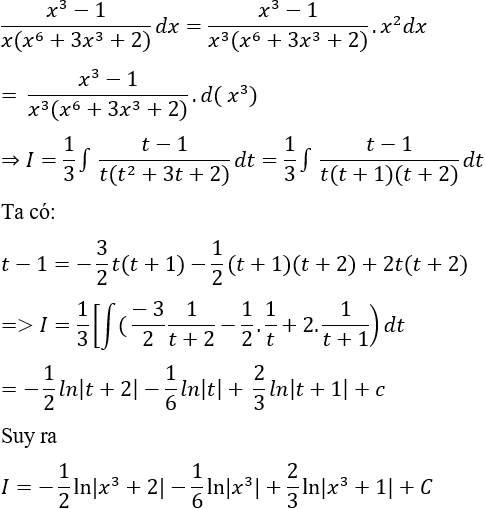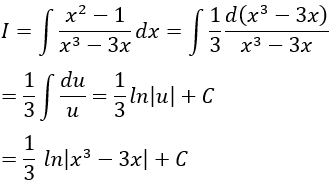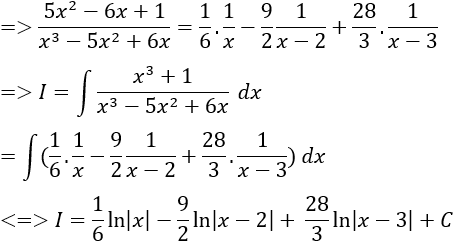Tìm nguyên hàm của hàm phân thức bằng phương pháp đổi biến số
1. Phương pháp giải
Cho hàm số u = u(x) có đạo hàm liên tục trên K và hàm số y = f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó nếu F là một nguyên hàm của f thì:
2. Ví dụ minh họa
Ví dụ 1. Tính
Lời giải
Ta có:
Đặt u = 5x - 2 ta có:
Chọn B.
Ví dụ 2. Tính
A. 2ln|x2 - x| + C.
B. xln|x2 - x| + C.
C. ln|x2 - x| + C.
D. Đáp án khác.
Lời giải
Ta có:
Đặt u = x2 - x khi đó:
Chọn C.
Ví dụ 3. Tính
Lời giải
Chọn C.
Ví dụ 4. Tính
Lời giải
Ta có:
Chọn A.
Ví dụ 5. Tính
Lời giải
Ta có:
Chọn A.
Ví dụ 6. Tính
Lời giải
Chọn A.
Ví dụ 7. Tính
Lời giải
Ta có:
Chọn A.
Ví dụ 8. Tính
Lời giải
Đặt t = x + 3 ⇒ x = t - 3 và dx = dt.
Khi đó:
Chọn A.
Ví dụ 9. Tính
Lời giải
Chọn D.
Ví dụ 10. Tính
A. 2x - 2ln|x+1| + c.
B. x2 + 2ln|x+1| + c.
C. x2 - 2ln|x+1| + c.
D. Tất cả sai.
Lời giải
Ta có:
Chọn C.
Ví dụ 11. Tính
Lời giải
Chọn D.
Ví dụ 12. Tính
Lời giải
Ta có: x3 + x2 - 2x = x(x - 1)(x + 2)
Giả sử:
⇔ 2x2 - 5x - 3 = A(x - 1).(x + 2) + B.x.(x + 2) + Cx.(x - 1) (*)
* Phương pháp gán các giá trị đặc biệt vào (*)
Thay x = 0 vào (*) suy ra: 2A = 3 ⇒ A = 3/2
Thay x = 1 vào (*) suy ra: 3B = -6 ⇒ B = -2
Thay x = -2n vào (*) suy ra: 6C = 15 ⇒ C = 5/2
Chọn A.
Ví dụ 13. Tính
Lời giải
Ta có:
Chọn B.
3. Bài tập vận dụng (có đáp án)
Câu 1: Tính
Lời giải:
Chọn C.
Câu 2: Tính
Lời giải:
Ta có:
Chọn A.
Câu 3: Tính
Lời giải:
Đặt t = x3 ⇒ dt = 3x2 dx
Ta có:
Chọn B.
Câu 4: Tính
Lời giải:
Chọn B.
Câu 5: Tính
Lời giải:
Ta có:
Đặt u = x3 - 3x khi đó:
Chọn C.
Câu 6: Tính
Lời giải:
Ta có:
Chọn C.
Câu 7: Tìm nguyên hàm:
Lời giải:
Chọn A.
Câu 8: Một nguyên hàm của hàm số 
Lời giải:
Ta có:
Cho C = 0 ta được một nguyên hàm của hàm số f(x) là:
Chọn A.
Câu 9: Tính
Lời giải:
Ta có:
Do đó:
Chọn D.
Câu 10: Tìm nguyên hàm của hàm số
Lời giải:
Ta có:
Chọn D.
Câu 11: Tìm nguyên hàm của hàm số
Lời giải:
Ta có:
Chọn B.
Câu 12: Tính
Lời giải:
Ta có: x3 - 5x2 + 6x = x.(x - 2).(x - 3)
+ Giả sử:
⇔ 5x2 - 6x + 1 = A(x - 2)(x - 3) + Bx.(x - 3) + Cx(x - 2) (*)
Thay x = 0 vào (*) ta được: 1 = 6A ⇒ A = 1/6
Thay x = 2 vào (*) ta được: 9 = -2B ⇒ B = -9/2
Thay x = 3 vào(*) ta được: 28 = 3C ⇒ C = 28/3
Chọn D.
Câu 13: Tính
Lời giải:
Ta có: x3 - 3x + 2 = (x - 1)2(x + 2)
Giả sử:
⇒ 3x2 + 3x + 3 = A(x + 2)+ B(x - 1).(x + 2) + C(x - 1)2 (*)
+ Gán các giá trị đặc biệt vào (*):
Cho x = 1 ⇒ 3A = 9 nên A = 3
Cho x = -2 ⇒ 9C = 9 nên C = 1
Cho x = 0 ⇒ 3 = 2A - 2B + C ⇒ B = 2
Vậy:
Chọn A.
Xem thêm các dạng bài tập liên quan khác:
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án
40 Bài tập Tìm nguyên hàm bằng phương pháp đổi biến số (2024) cực hay
30 Bài tập Tìm nguyên hàm của hàm đa thức bằng phương pháp đổi biến số (2024) cực hay, có đáp án