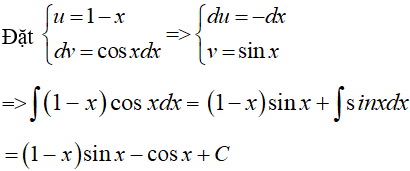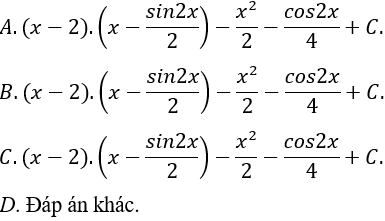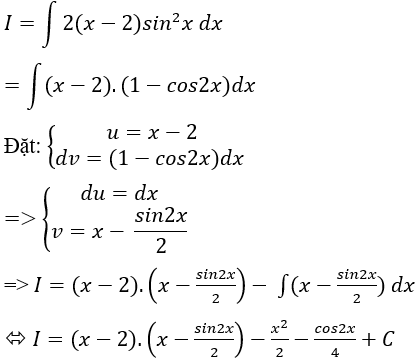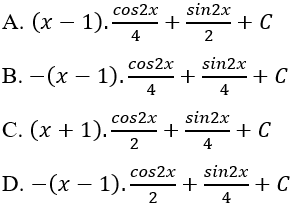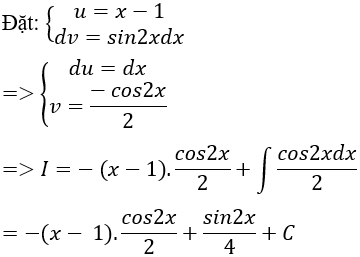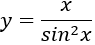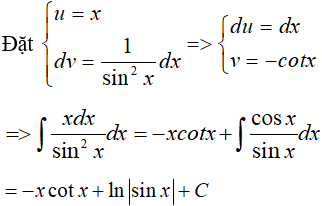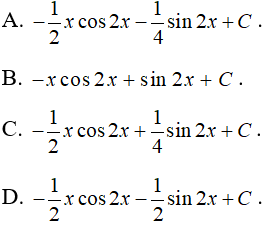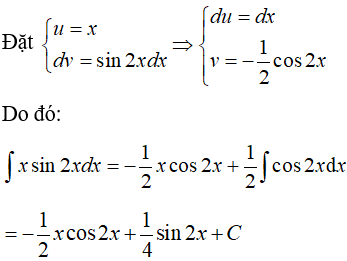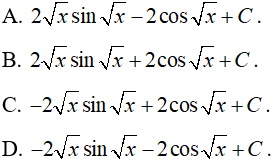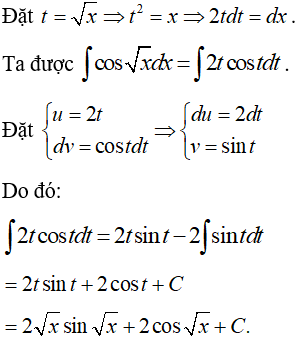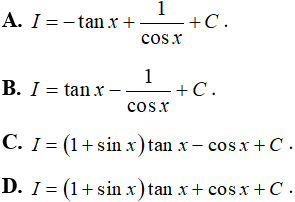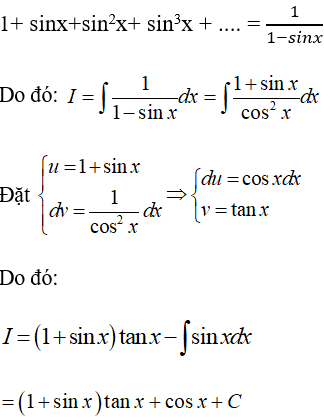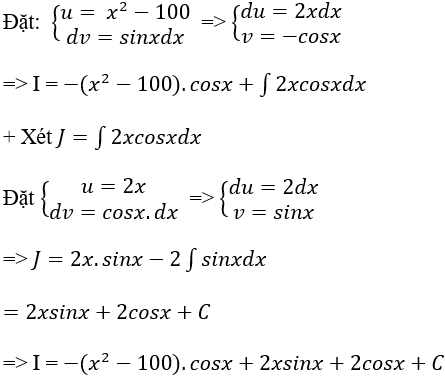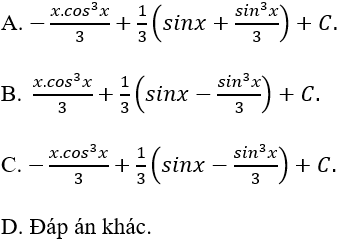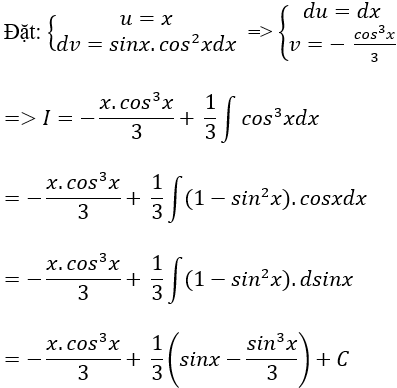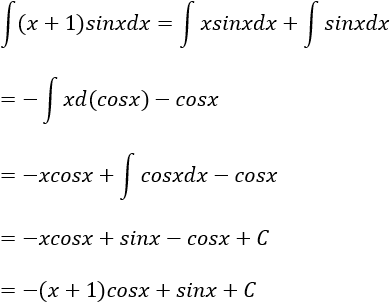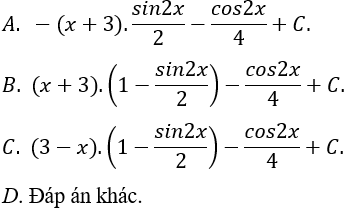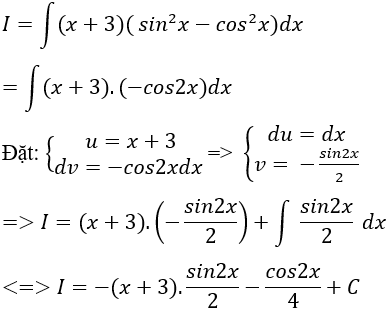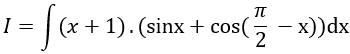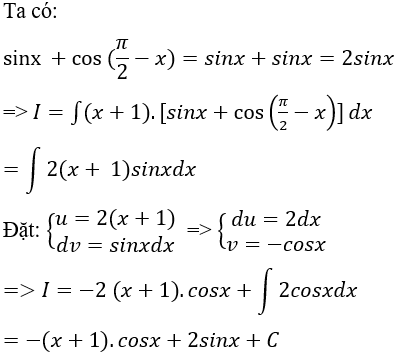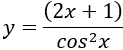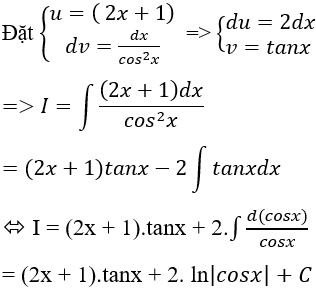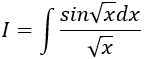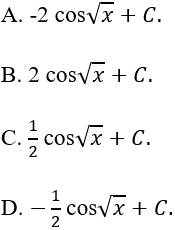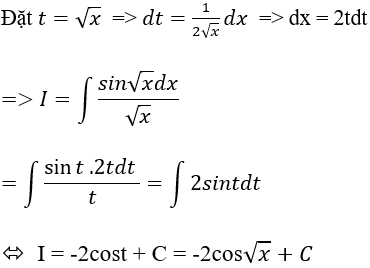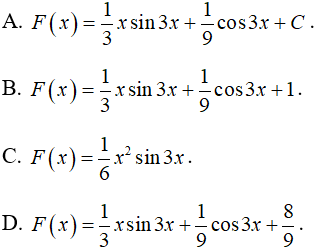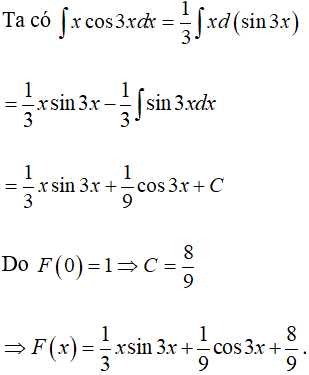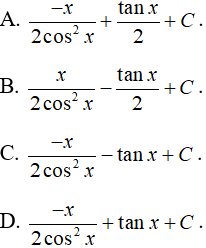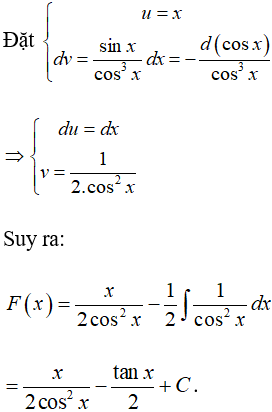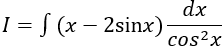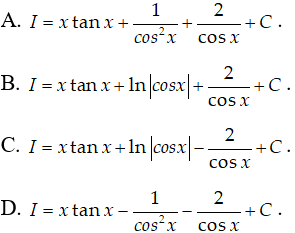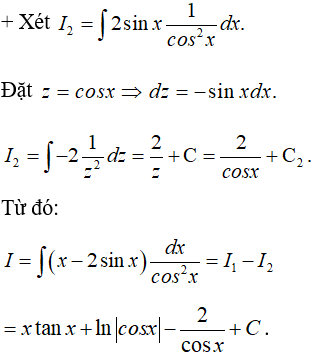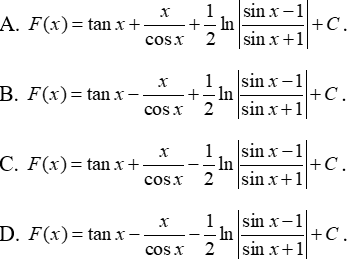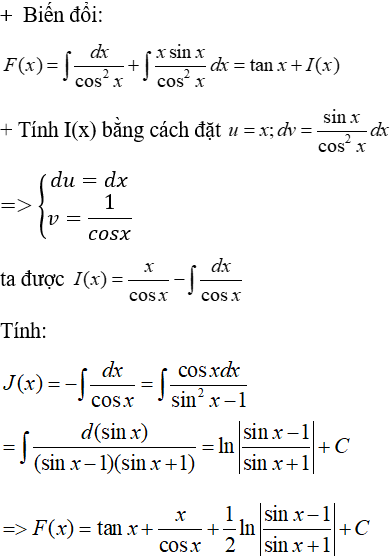Tìm nguyên hàm của hàm lượng giác bằng phương pháp
nguyên hàm từng phần
1. Phương pháp giải
a. Định lí
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì ∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx. Viết gọn: ∫udv = uv - ∫vdu.
b. Cách đặt
Các dạng cơ bản: Giả sử cần tính I = ∫P(x).Q(x)dx
* Thông thường nên chú ý: “Nhất log, nhì đa, tam lượng, tứ mũ”
Cho I = ∫f(x).g(x)dx trong đó f(x) là đa thức và g(x) là biểu thức lượng giác.
Ta đặt u = f(x) và v’ = g(x).
Sau đó áp dụng công thức lấy nguyên hàm từng phần.
2. Ví dụ minh họa
Ví dụ 1. Tìm nguyên hàm của hàm số sau: ∫(1 - x)cosxdx
A. (1 + x)cosx - sinx + C.
B. (1 - x)sinx - cosx + C.
C. (1 - x)cosx + sinx + C.
D. (1 - x)cosx - cosx + C.
Lời giải
Chọn B.
Ví dụ 2. Tìm nguyên hàm của hàm số: y = 2(x - 2).sin2x
Lời giải
Ta có: 2(x - 2).sin2x = (x - 2).(1 - cos2x) vì (cos2x = 1- 2sin2x)
Chọn A.
Ví dụ 3. Tính I = ∫(2x - 2).sinx.cosxdx
Lời giải
Ta có: (2x - 2).sinx.cosx = (x - 1).2sinx.cosx = (x - 1).sin2x
⇒ I = ∫(2x - 2).sinx.cosxdx = ∫(x - 1)sin2xdx
Chọn D.
Ví dụ 4. Tìm nguyên hàm của các hàm số sau
A. -x.cotx + ln|sinx| + C.
B. x.cotx + ln|sinx| + C.
C. x.cosx + ln|sinx| + C.
D. x.cotx - ln|sinx| + C.
Lời giải
Chọn A.
Ví dụ 5. Tính ∫xsin2xdx.
Lời giải
Chọn C.
Ví dụ 6. Tính ∫cos√x dx.
Lời giải
Chọn B.
Ví dụ 7. Tính I = ∫(1 + sinx + sin2x + sin3x + ...)dx.
Lời giải
Ta có: 1 + sinx + sin2x + sin3x + ... là tổng của cấp số nhân với un = sinnx
Vì |sinx| ≤ 1 nên áp dụng công thức tính tổng của cấp số nhân có công bội q = sinx < 1 ta được:
Chọn D.
Ví dụ 8. Tính I = ∫(x2 - 100)sinxdx
A. I = -(x2 - 100).sinx + 2xsinx - 2cosx + C.
B. I = (x2 - 100).cosx - 2xsinx + cosx + C.
C. I = -(x2 - 100).cosx + 2xsinx + 2cosx + C.
D. Tất cả sai.
Lời giải
Chọn C.
Ví dụ 9. Tính I = ∫x.sinx.cos2xdx
Lời giải
Chọn C.
3. Bài tập vận dụng (có đáp án)
Câu 1: Tính nguyên hàm của hàm số: f(x) = (x + 1).sinx
A. F(x) = (x + 1)cosx + sinx + c.
B. F(x) = -(x + 1)cosx + sinx + c.
C. F(x) = -(x + 1)cosx - sinx + c.
D. F(x) = -(x + 1)cosx - sinx + c.
Lời giải:
Ta có:
Chọn B.
Câu 2: Tìm nguyên hàm của hàm số: y = (x + 3).(sin2x - cos2x)
Lời giải:
Ta có: (x + 3).(sin2x – cos2x) = (x + 3).(-cos2x) vì (cos2x = cos2x - sin2x)
Chọn A.
Câu 3: Tính:
A. (x + 1).cosx + 2sin2x + C.
B. 2(x + 1).sinx + 2cosx + C.
C. (x + 1).cosx + 2cosx + C.
D. -(x + 1).cosx + 2sinx + C.
Lời giải:
Chọn D.
Câu 4: Tìm nguyên hàm của các hàm số sau
A. (2x + 1).tanx + 2.ln|cosx| + C.
B. (2x + 1).cotx + 2.ln|cosx| + C.
C. (2x + 1).sinx + 2.ln|sinx| + C.
D. Đáp án khác.
Lời giải:
Chọn A.
Câu 5: Tính
Lời giải:
Chọn A.
Câu 6: Gọi hàm số F(x) là một nguyên hàm của f(x) = xcos3x, biết F(0) = 1. Vậy F(x) là:
Lời giải:
Chọn D.
Câu 7: Nguyên hàm của hàm số 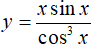
Lời giải:
Chọn B.
Câu 8: Tìm
Lời giải:
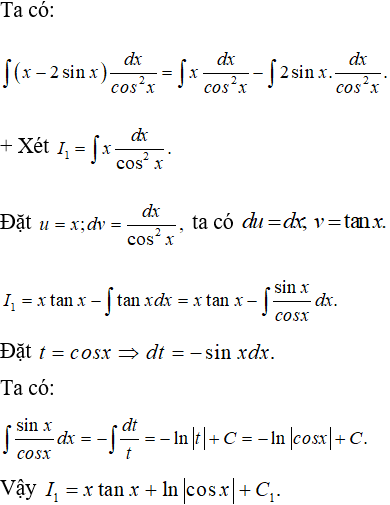
Chọn C.
Câu 9: Tính 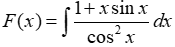
Lời giải:
Chọn A.
Xem thêm các dạng bài tập toán hay khác:
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án
40 Bài tập Tìm nguyên hàm bằng phương pháp đổi biến số (2024) cực hay
30 Bài tập Tìm nguyên hàm của hàm đa thức bằng phương pháp đổi biến số (2024) cực hay, có đáp án
40 Bài tập Tìm nguyên hàm của hàm phân thức bằng phương pháp đổi biến số (2024) cực hay, có đáp án