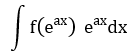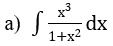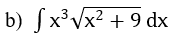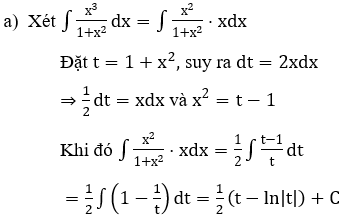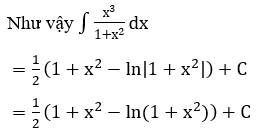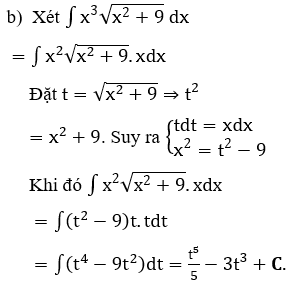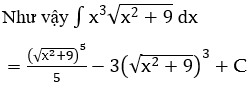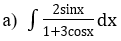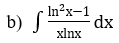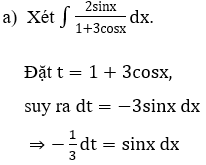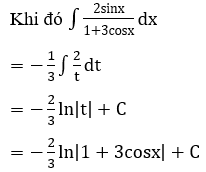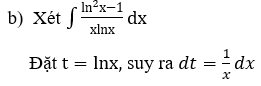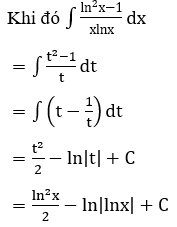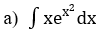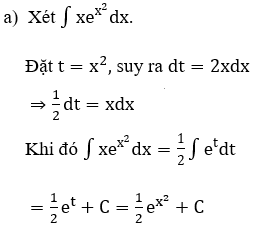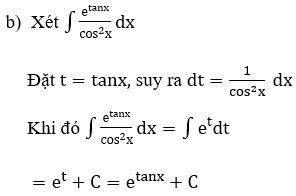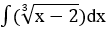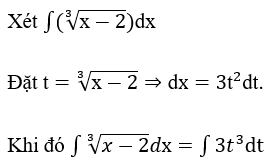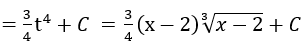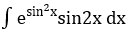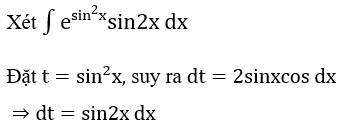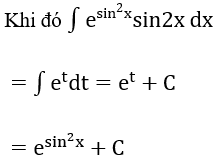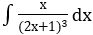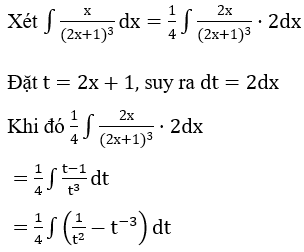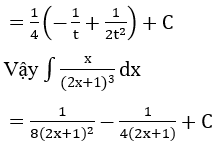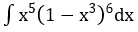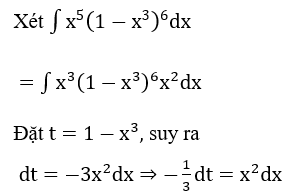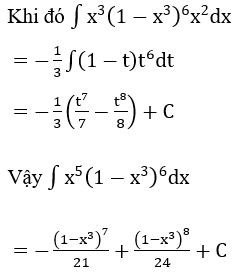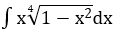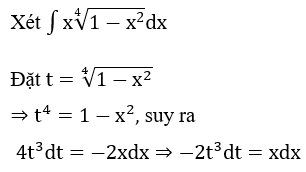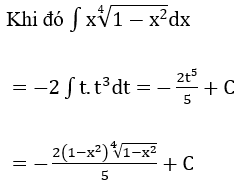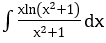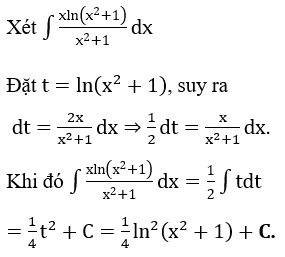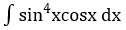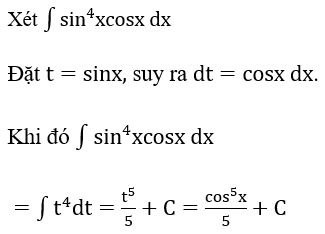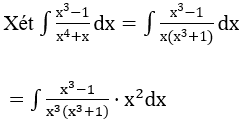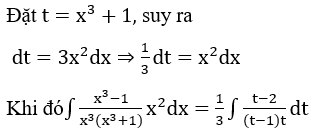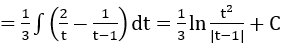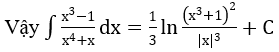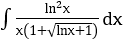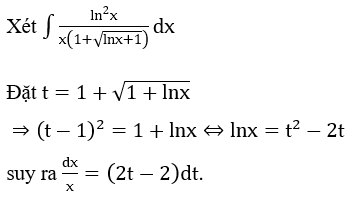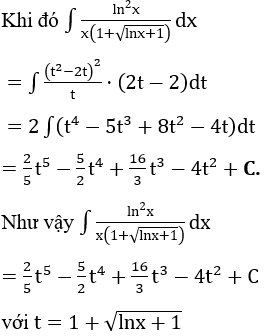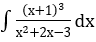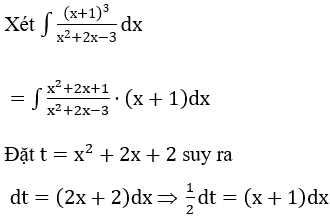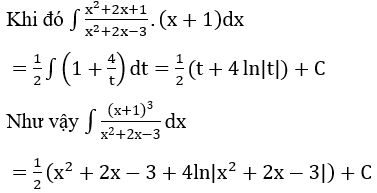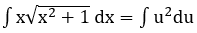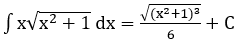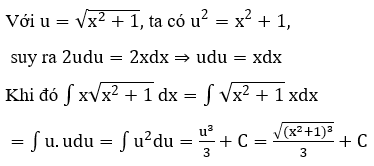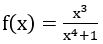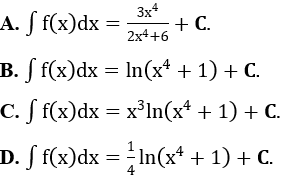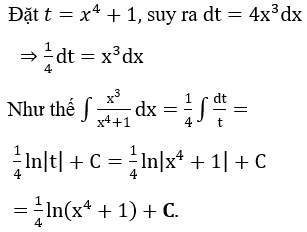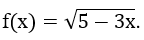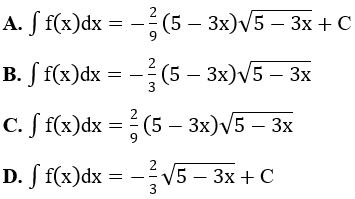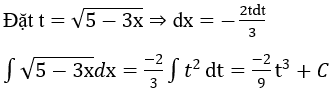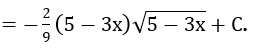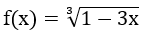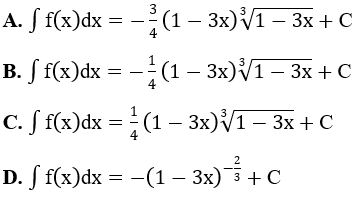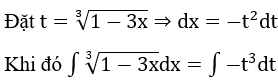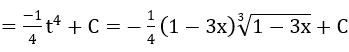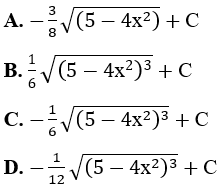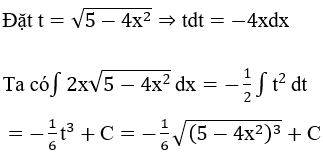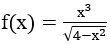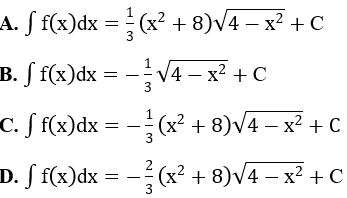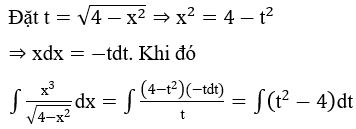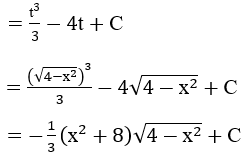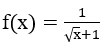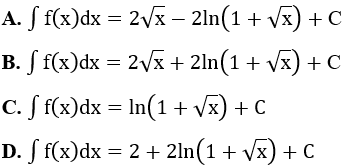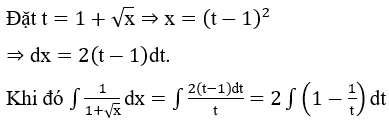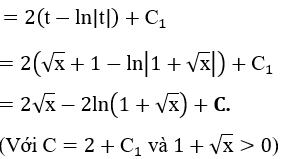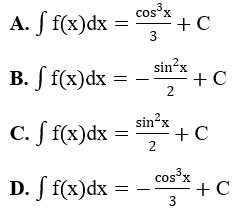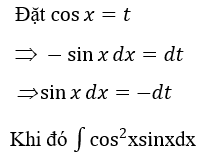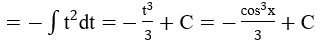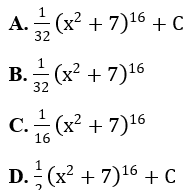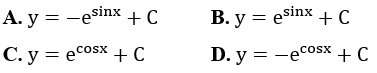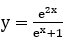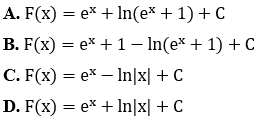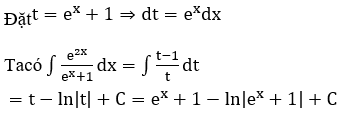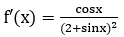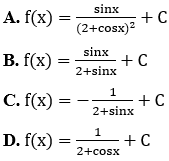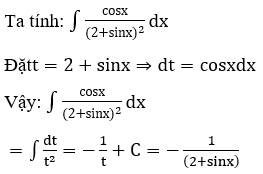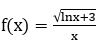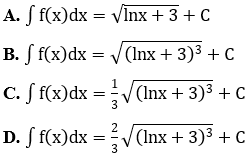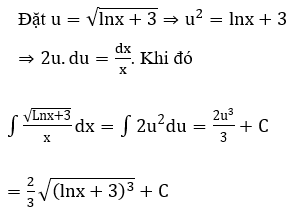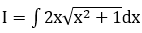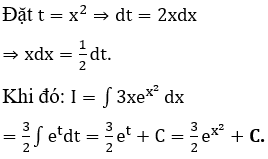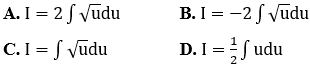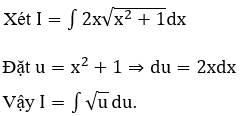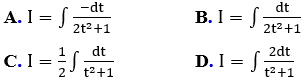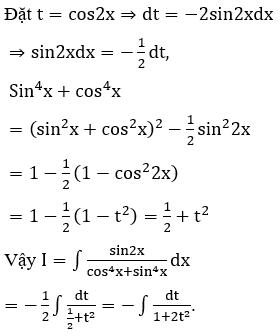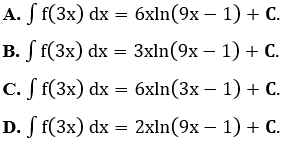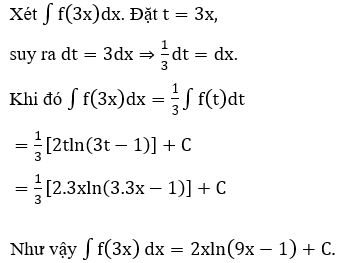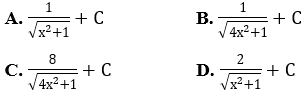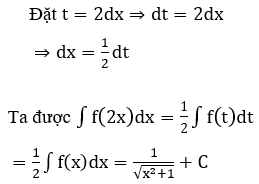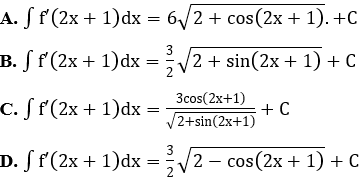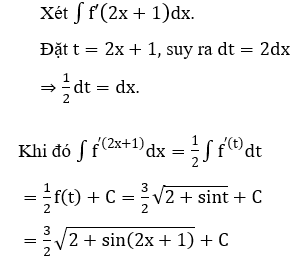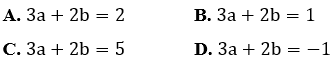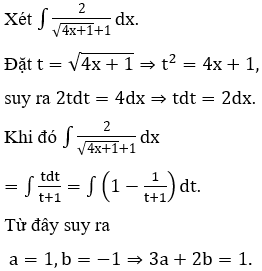Tìm nguyên hàm bằng phương pháp đổi biến số
1. Phương pháp giải
|
STT |
Dạng tích phân |
Cách đặt |
Đặc điểm nhận dạng |
|
1 |
|
t = f(x) |
Biểu thức dưới mẫu |
|
2 |
|
t = t(x) |
Biểu thức ở phần số mũ |
|
3 |
|
t = t(x) |
Biểu thức trong dấu ngoặc |
|
4 |
|
|
Căn thức |
|
5 |
|
t = lnx |
dx/x đi kèm biểu thức theo lnx |
|
6 |
|
t = sinx |
cosx dx đi kèm biểu thức theo sinx |
|
7 |
|
t = cosx |
sinx dx đi kèm biểu thức theo cosx |
|
8 |
|
t = tanx |
|
|
9 |
|
t = cotx |
|
|
10 |
|
t = eax |
eax dx đi kèm biểu thức theo eax |
|
Đôi khi thay cách đặt t = t(x) bởi t = m.t(x) + n ta sẽ biến đổi dễ dàng hơn. |
|||
2. Ví dụ minh họa
Bài 1: Tìm các họ nguyên hàm sau đây:
Lời giải:
Bài 2: Tìm các họ nguyên hàm sau đây:
Lời giải:
Bài 3: Tìm các họ nguyên hàm sau đây:
Lời giải:
3. Bài tập vận dụng (có đáp án)
Bài 1: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 2: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 3: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 4: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 5: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 6: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 7: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 8: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 9: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 10: Tìm họ nguyên hàm của hàm số
Lời giải:
4. Bài tập tự luyện (có đáp án)
Bài 1: Khi tìm họ nguyên hàm 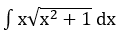
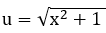
+ Khẳng định 1: du = dx
+ Khẳng định 2:
+ Khẳng định 3:
Hỏi có tất cả bao nhiêu khẳng định đúng trong các khẳng định nêu trên ?
A. 0 B. 1 C. 2 D. 3
Lời giải:
Đáp án : B
Giải thích :
Vậy chỉ có khẳng định 2 là đúng
Bài 2: Tìm nguyên hàm của hàm số
Lời giải:
Đáp án : D
Giải thích :
Bài 3: Tìm nguyên hàm của hàm số
Lời giải:
Đáp án : A
Giải thích :
Bài 4: Tìm nguyên hàm của hàm số
Lời giải:
Đáp án : B
Giải thích :
Bài 5: Kết quả tính 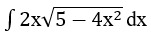
Lời giải:
Đáp án : C
Giải thích :
Bài 6: Tìm nguyên hàm của hàm số
Lời giải:
Đáp án : C
Giải thích :
Bài 7: Tìm nguyên hàm của hàm số
Lời giải:
Đáp án : A
Giải thích :
Bài 8: Tìm nguyên hàm của hàm số f(x)=cos2x.sinx
Lời giải:
Đáp án : D
Giải thích :
Bài 9: Kết quả của I = ∫x(x2+7)15dx là :
Lời giải:
Đáp án : A
Giải thích :
Bài 10: Nguyên hàm của hàm số y=-ecosxsinx là:
Lời giải:
Đáp án : C
Giải thích :
Xét -∫ecosxsinxdx, bằng cách đặt t = cosx ta có dt = -sinxdx nên
-∫ecosxsinxdx = ∫etdt = - et + C = ecosx + C.
Bài 11: Hàm số nào sau đây là một nguyên hàm của hàm số
Lời giải:
Đáp án :
Giải thích :
Bài 12: Tìm các hàm số f(x) biết rằng
Lời giải:
Bài 13: Tìm nguyên hàm của hàm số
Lời giải:
Bài 14: Một nguyên hàm của hàm số f(x) = 3x.ex2 là:
Lời giải:
Đáp án :
Giải thích :
Bài 15: Tính 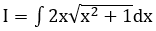
Lời giải:
Bài 16: Cho 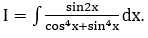
Lời giải:
Bài 17: Biết ∫f(x) dx = 2xln(3x-1) + C. Tìm khẳng định đúng trong các khẳng định bên dưới?
Lời giải:
Bài 18: Cho 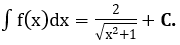
Lời giải:
Bài 19: Cho hàm số 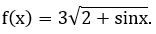
Lời giải:
Bài 20: Với phép đặt 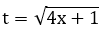
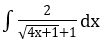
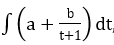
Lời giải:
Xem thêm các dạng bài tập liên quan khác:
Lý thuyết Nguyên hàm từng phần và các dạng bài tập (có đáp án) chi tiết nhất 2024
60 Bài tập về Tích phân (có đáp án năm 2024)
60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2023)


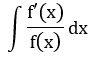

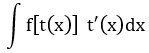
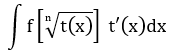
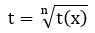
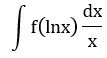
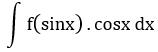
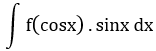
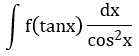
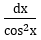 đi kèm biểu thức theo tanx
đi kèm biểu thức theo tanx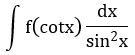
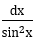 đi kèm biểu thức theo cotx
đi kèm biểu thức theo cotx