Dạng 1. Sử dụng định lí Pythagore chứng minh tam giác vuông
-
278 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
 Xem đáp án
Xem đáp án
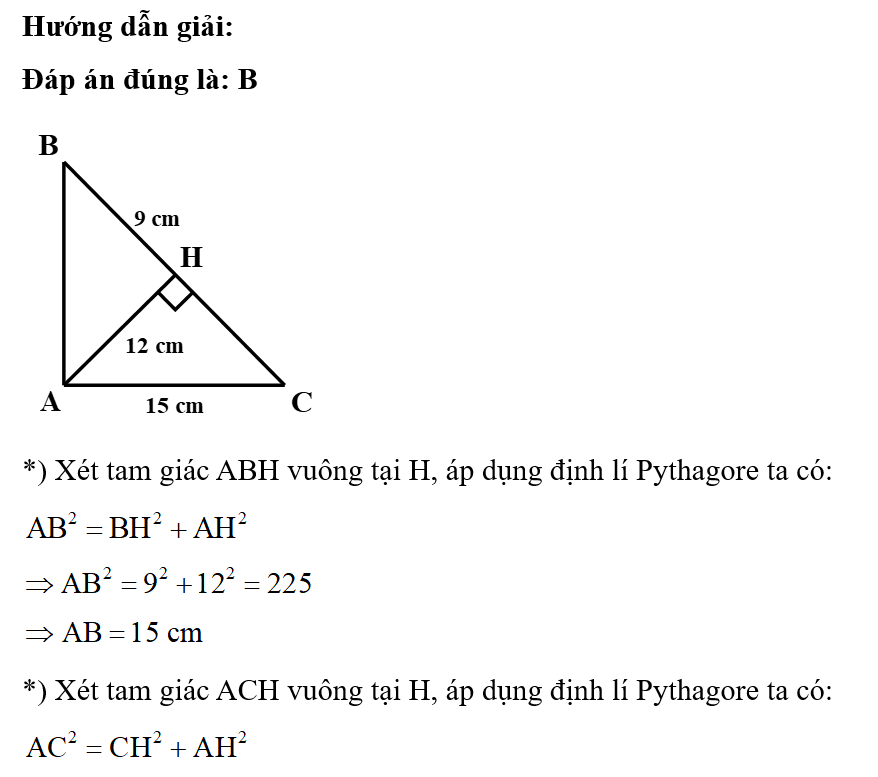
Hướng dẫn giải:
Đáp án đúng là: C
+) Vì nên tam giác có độ dài ba cạnh 11 cm; 7 cm; 8 cm không phải là tam giác vuông.
Þ Đáp án A sai
+) Vì nên tam giác có độ dài ba cạnh 12 dm; 15 dm; 18 dm không phải là tam giác vuông.
Þ Đáp án B sai
+) Vì nên tam giác có độ dài ba cạnh 9 m; 12 m; 15 m là tam giác vuông (định lí Pythagore đảo).
Þ Đáp án C đúng
+) Vì nên tam giác có độ dài ba cạnh 6 m; 7 m; 9 m không phải là tam giác vuông.
Þ Đáp án D sai
Câu 3:
Xét các khẳng định sau:
I) Tam giác có độ dài ba cạnh là 6 cm, 10 cm, 8 cm là tam giác vuông.
II) Tam giác có độ dài ba cạnh là 8 cm, 10 cm, 8 cm không phải là tam giác vuông.
Chọn câu trả lời đúng.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
*) Vì nên tam giác có độ dài ba cạnh là 6 cm, 10 cm, 8 cm là tam giác vuông (định lí Pythagore đảo).
Þ I) đúng
*) Vì nên tam giác có độ dài ba cạnh là 8 cm, 10 cm, 8 cm không phải là tam giác vuông.
Þ II) đúng
Vậy cả I) và II) đều đúng.
Câu 5:
Cho các bộ ba số sau:
(a) 1 cm, 2 cm, 2 cm;
(b) 2 cm, 4 cm, 20 cm;
(c) 5 cm, 4 cm, 3 cm;
(d) 2 cm, 2 cm,
Có bao nhiêu bộ ba số đo là độ dài ba cạnh của một tam giác vuông?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
*) Vì nên tam giác có độ dài ba cạnh là 1 cm, 2 cm, 2 cm không phải tam giác vuông.
*) Vì nên tam giác có độ dài ba cạnh là 2 cm, 4 cm, 20 cm không phải tam giác vuông.
*) Vì nên tam giác có độ dài ba cạnh là 5 cm, 4 cm, 3 cm là tam giác vuông (định lí Pythagore đảo).
*) Vì nên tam giác có độ dài ba cạnh là 2 cm, 2 cm, là tam giác vuông (định lí Pythagore đảo).
Vậy có 2 bộ ba số đo là độ dài ba cạnh của một tam giác vuông.
Câu 7:
Cho tam giác DEF có DE = 2 cm, . Để tam giác DEF vuông tại D thì độ dài của cạnh DF là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Áp dụng định lí Pythagore đảo, để tam giác DEF vuông tại D thì:
Vậy để tam giác DEF vuông tại D thì độ dài của cạnh DF là .
Câu 8:
Một khung gỗ ABCD được tạo thành từ 5 thanh nẹp có độ dài như sau:
AB = CD = 48 cm
BC = AD = 36 cm
AC = 60 cm
Kết luận nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
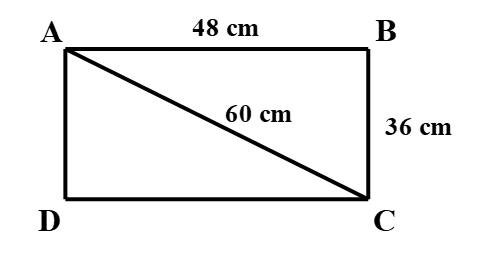
*) Tứ giác ABCD có:
AB = CD = 48 cm
BC = AD = 36 cm
Þ Tứ giác ABCD là hình bình hành.
*) Xét tam giác ABC ta có:
Þ Tam giác ABC vuông tại B (định lí Pythagore đảo)
*) Hình bình hành ABCD có nên ABCD là hình chữ nhật (dấu hiệu nhận biết).
Vậy tứ giác ABCD là hình chữ nhật
Câu 9:
Một khung gỗ ABCD được tạo thành từ 5 thanh nẹp có độ dài như sau:
AB = CD = 48 cm
BC = AD = 36 cm
AC = 60 cm
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D

*) Tứ giác ABCD có:
AB = CD = 48 cm
BC = AD = 36 cm
Þ Tứ giác ABCD là hình bình hành.
*) Xét tam giác ABC ta có:
Þ Tam giác ABC vuông tại B (định lí Pythagore đảo)
*) Hình bình hành ABCD có nên ABCD là hình chữ nhật (dấu hiệu nhận biết).
Vậy tứ giác ABCD là hình chữ nhật
Suy ra, .