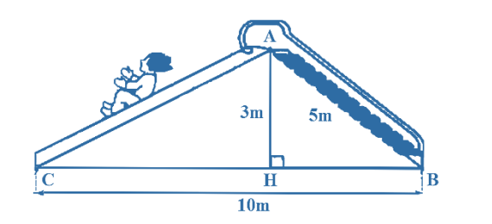
Dạng 4. Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore
-
220 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Hình dưới đây mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m.
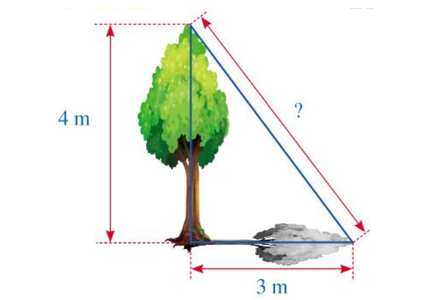
Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
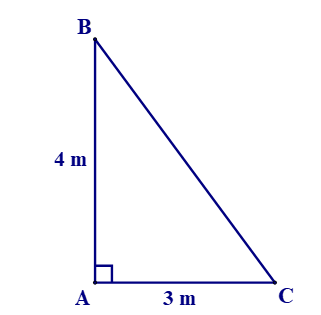
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AB2 + AC2 = 42 + 32 = 25
BC = 5 m
Vậy khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây là 5 m.
Câu 2:
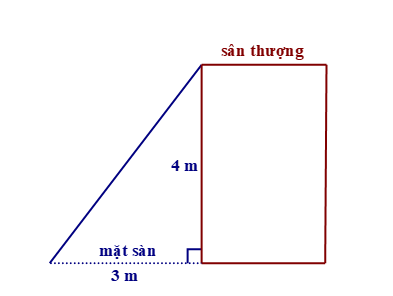
Bác thợ muốn xây một cầu thang bắc từ mặt sàn lên sân thượng. Biết rằng bức tường từ sàn lên sân thượng cao 4 m, chân cầu thang cách bức tường 3 m. Khi đó, chiều dài của cầu thang là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
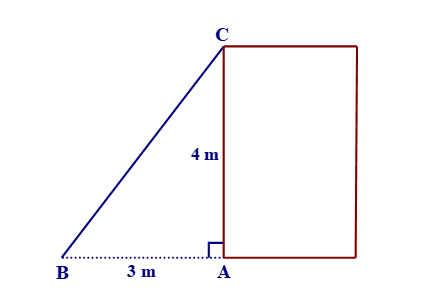
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AC2 + AB2 = 42 + 32 = 25
BC = 5 m.
Câu 3:
Một chiếc cầu thang có các kích thước như hình vẽ sau:
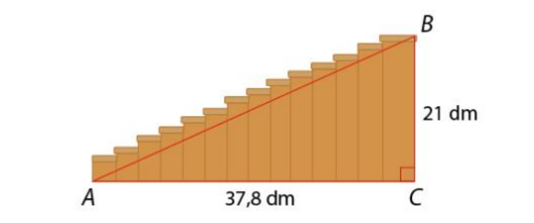
Tính độ dài đoạn thẳng AB.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Xét tam giác ABC vuông tại C, áp dụng định lý Pythagore ta có:
AB2 = BC2 + AC2 = 212 + 37,82 = 1 869,84
AB 43,2 dm
Vậy độ dài AB là 43,2 dm.
Câu 4:
Hình dưới đây mô tả một thanh gỗ dài 2,6 m đặt dựa vào một bức tường thẳng đứng. Chân thanh gỗ cách mép tường một khoảng là 1 m. Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?
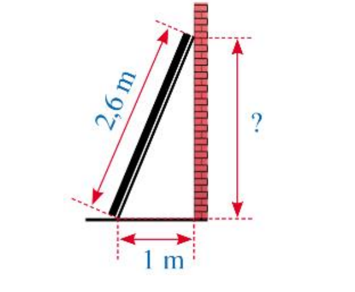
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
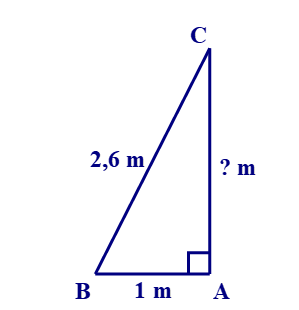
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AC2 + AB2
AC2 = BC2 – AB2 = 2,62 – 12 = 5,76
AC = 2,4 m.
Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là 2,4 m.
Câu 6:
Nhà bạn An (vị trí A trên hình vẽ) cách nhà bạn Châu (vị trí C trên hình vẽ) 600 m và cách nhà bạn Bình (vị trí B trên hình vẽ) 450 m. Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Bình đến nhà Châu.
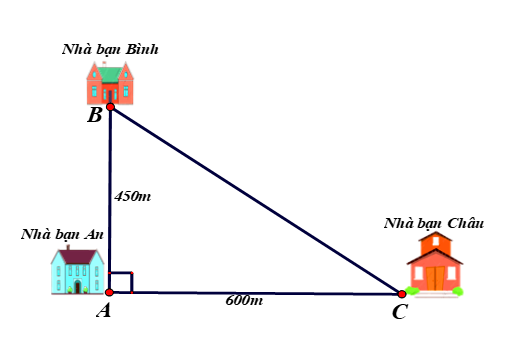
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AB2 + AC2 = 4502 + 6002 = 562 500
BC = 750 m
Vậy khoảng cách từ nhà bạn Bình đến nhà bạn Châu là 750 m.
Câu 7:
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy được 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp người khách tại điểm D. Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu ki-lô-mét?
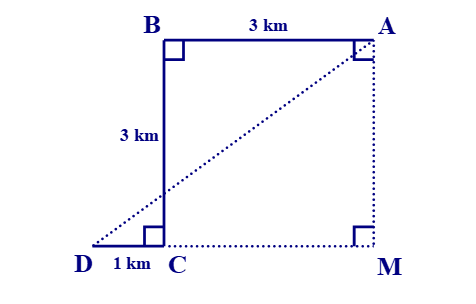
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
*) Quan sát hình vẽ, ta thấy ABCM là hình vuông.
Suy ra AM = MC = CB = BA = 3 km.
*) DM = DC + CM = 1 km + 3 km = 4 km.
*) Xét tam giác AMD vuông tại M, áp dụng định lí Pythagore ta có:
AD2 = AM2 + DM2 = 32 + 42 = 25
AD = 5 km.
Câu 8:
Cho hình vẽ:
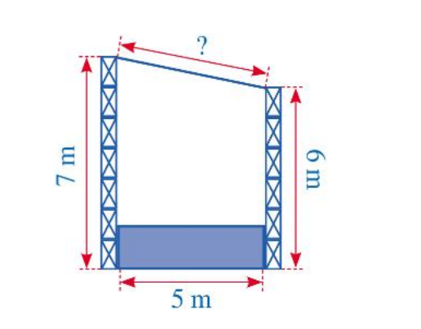
Hình vẽ trên mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng 7 m, chiều cao của khung phía sau là 6 m, hai khung cách nhau một khoảng 5 m. Chiều dài của mái che sân khấu khoảng … mét.
Số thích hợp để điền vào chỗ chấm là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
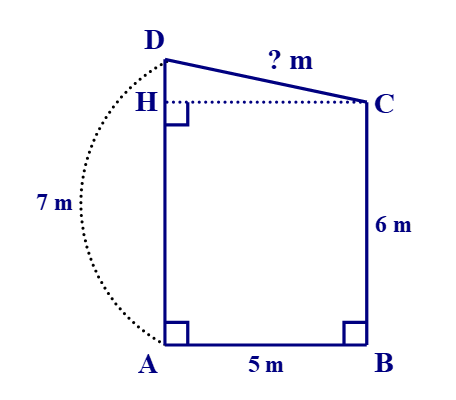
*) AHCB là hình chữ nhật, có AH = BC = 6 cm; HC = AB = 5 m.
*) HD = AD – AH = 7 cm – 6 cm = 1 cm.
Xét tam giác DHC vuông tại H, ta có:
DC2 = DH2 + CH2 = 12 + 52 = 26
Vậy chiều dài mái che sân khấu khoảng 5,1 m.
Câu 9:
Hình dưới đây mô tả một cánh buồm có dạng tam giác vuông, được buộc vào cột buồm thẳng đứng, với độ dài hai cạnh góc vuông là 12 m và 5 m.
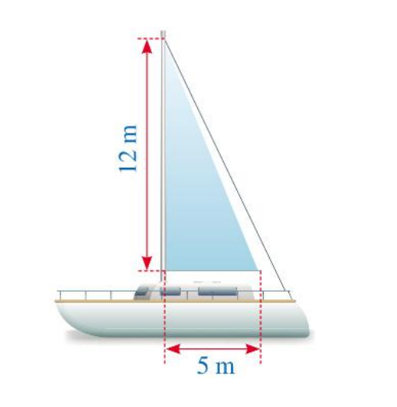
Chu vi của cánh buồm là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
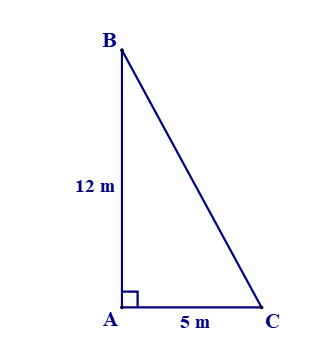
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AB2 + AC2 = 122 + 52 = 169
BC = 13 m
Chu vi của tam giác ABC là:
13 + 12 + 5 = 30 (m)
Vậy chu vi của cánh buồm là 30 m.
