Trắc nghiệm Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án
Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều
-
500 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC cân tại A, đường trung tuyến AM. Biết số đo là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
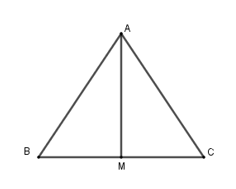
Vì ΔABC cân tại A nên đường trung tuyến AM đồng thời là đường phân giác của ∆ABC.
Do đó
Câu 2:
Cho tam giác ABC, AM là đường trung tuyến. Biết AM = MB = MC. Cho biết tam giác ABC là tam giác gì?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
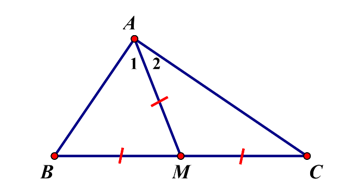
Xét ∆AMB có MA = MB (giả thiết) suy ra ∆AMB cân tại M nên .
Xét ∆AMC có MA = MC (giả thiết) suy ra ∆AMC cân tại M nên .
Do đó
Mặt khác: (tổng ba góc của một tam giác)
Suy ra hay .
Do đó:
Vậy ΔABC vuông tại A.
Câu 3:
Cho tam giác ABC cân tại A. Vẽ AH ⊥ BC. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Điểm C là trọng tâm của tam giác nào?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
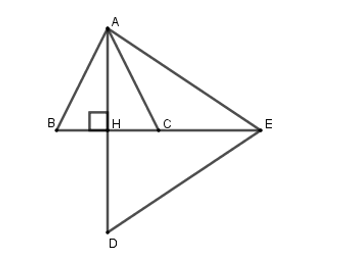
Xét ∆AHB (vuông tại H) và AHC (vuông tại H) có:
AB = AC (do ΔABC cân tại A);
AH là cạnh chung
Do đó: ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)
Suy ra HB = HC (hai cạnh tương ứng)
Ta có CE = CB = HB + HC = 2CH
Xét ΔADE có EH là đường trung tuyến mà CE = 2CH nên C là trọng tâm của ΔADE.
Câu 4:
Cho ΔABC có hai đường trung tuyến BN, CP vuông góc với nhau tại G. Biết độ dài BC = 5cm. Độ dài AG là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
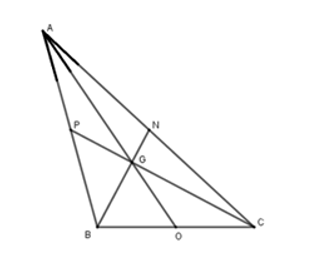
Xét ∆ABC có hai đường trung tuyến BN, CP cắt nhau tại G nên G là trọng tâm của ∆ABC. Do đó AG là đường trung tuyến thứ ba của tam giác.
Giả sử AG cắt BC tại O.
Khi đó O là trung điểm của BC nên GO là đường trung tuyến của ∆GBC.
Xét ΔBGC vuông tại G (do có GO là đường trung tuyến của ∆GBC nên theo kết quả của Ví dụ 2, ta suy ra
Mà (do G là trọng tâm của ∆ABC)
Suy ra AG = BC = 5 (cm).
Câu 5:
Cho ΔABC vuông tại A, trung tuyến AM. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
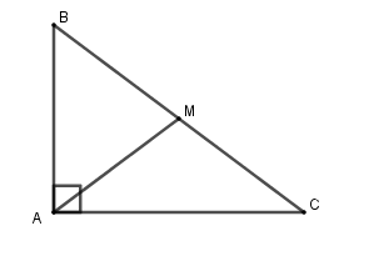
Ta có ΔABC vuông tại A và trung tuyến AM ứng với cạnh huyền BC nên theo kết quả của Ví dụ 2, ta có hay BC = 2AM.
Xét ΔABC có BC < AB + AC (bất đẳng thức tam giác)
Suy ra 2AM < AB + AC hay
Câu 7:
Cho ΔABC cân tại A có hai đường trung tuyến BM, CN cắt nhau tại G. Tam giác GBC là tam giác
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
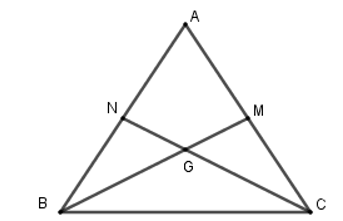
Vì ΔABC cân tại A nên AB = AC.
Ta có M là trung điểm của AC suy ra .
Ta có N là trung điểm của AC suy ra .
Do đó: AM = MC = AN = NB.
Xét ΔABM và ΔACN có:
AB = AC (chứng minh trên);
là góc chung;
AM = AN (chứng minh trên)
Do đó ΔABM và ΔACN (c.g.c)
Suy ra BM = CN (hai cạnh tương ứng)
Vì G là trọng tâm của ΔABC nên
Do đó BG = CG hay tam giác BGC cân tại G.
Câu 8:
Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho BD = CE. Khi đó tam giác ABC là tam giác
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
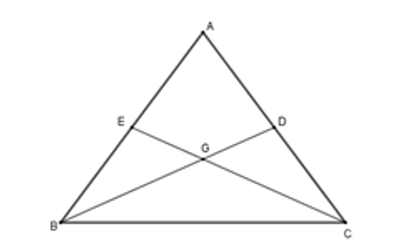
Hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm của ΔABC.
Suy ra mà BD = CE
Do đó BG = CG.
Khi đó BD – BG = CE – CG hay GD = GE.
Xét ΔBGE và ΔCGD có:
BG = CG (chứng minh trên);
(hai góc đối đỉnh);
GE = GD (chứng minh trên)
Do đó ΔBGE = ΔCGD (c.g.c)
Suy ra BE = CD (hai cạnh tương ứng).
Do BD và CE là hai đường trung tuyến của ∆ABC nên D, E lần lượt là trung điểm của AC, AB. Do đó và
Mà BE = CD (chứng minh trên) nên AB = AC, suy ra tam giác ABC cân tại A.
Câu 9:
Cho G là trọng tâm của tam giác đều ABC. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Các tia AG, BG và CG cắt BC, AC, AB lần lượt tại D, E, F thì D, E, F theo thứ tự là trung điểm của BC, AC, AB.
Mà BC = AC = AB (do tam giác ABC đều).
Do đó BD = DC = CE = EA = AF = FB.
Xét ΔAEB và ΔAFC có:
AB = AC (chứng minh trên);
là góc chung
AE = AF (chứng minh trên)
Do đó ΔAEB = ΔAFC (c.g.c).
Suy ra BE = CF (hai cạnh tương ứng) (1)
Chứng minh tương tự, ta có ΔBEC = ΔADC (c.g.c).
Suy ra BE = AD (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có AD = BE = CF (3)
Do G là trọng tâm của ΔABC nên ta có: (4)
Từ (3) và (4) suy ra GA = GB = GC.
Câu 10:
Cho tam giác ABC cân tại A. Đường phân giác của góc A cắt đường trung tuyến BD tại K. Gọi I là trung điểm của AB. Khẳng định nào sau đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
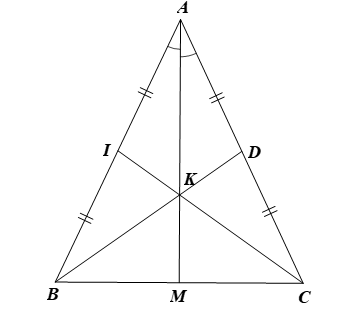
⦁ Gọi M là giao điểm của AK và BC.
Xét ∆AMB và ∆AMC có:
AB = AC (do ∆ABC cân tại A);
(do AM là phân giác của góc BAC);
AM là cạnh chung
Do đó ∆AMB = ∆AMC (c.g.c)
Suy ra MB = MC (hai cạnh tương ứng)
Khi đó AM hay AK là đường trung tuyến của tam giác ABC. Do đó khẳng định C đúng.
⦁ ∆ABC có hai đường trung tuyến AM, BD cắt nhau tại K nên K là trọng tâm của ∆ABC. Do đó khẳng định B đúng.
⦁ K là trọng tâm của ∆ABC nên CK là đường trung tuyến
Mà CI cũng là đường trung tuyến của ∆ABC nên ba điểm C, K, I thẳng hàng.
Do đó khẳng định A đúng.
⦁ Tam giác ABC có đường trung tuyến BD. Giả sử BD là đường phân giác của tam giác thì tam giác ABC cân tại B, điều này mâu thuẫn với giả thiết ∆ABC cân tại A.
Do đó khẳng định D là sai.
Vậy ta chọn phương án D.