10 câu hỏi trắc nghiệm thuộc Dạng 2. Chứng minh một điểm là trọng tâm của tam giác

Câu 1:

Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:

A. Trọng tâm của ΔABC;

B. Trọng tâm của ΔABE;

C. Trọng tâm của ΔABD;

D. Cách đều ba cạnh của ΔABC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

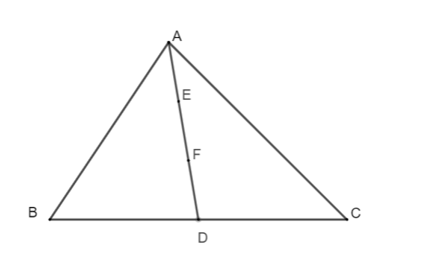
Cho tam giác tam giác ABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm (ảnh 1)

Ta có: AD = AE + EF + FD mà AE = EF = FD nên AD = 3AE.

Suy ra $A E = E F = F D = \frac{1}{3} A D$ .

Do đó $A F = A E + E F = \frac{1}{3} A D + \frac{1}{3} A D = \frac{2}{3} A D$

Vì AD là đường trung tuyến và $A F = \frac{2}{3} A D$ nên F là trọng tâm của ΔABC.

Câu 2:

Cho ΔABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho $B G = \frac{2}{3} B M$ và G là trung điểm của BK. Gọi E là trung điểm của CK, GE cắt AC tại I. Điểm I là trọng tâm của tam giác nào?

A. ΔKBC;

B. ΔABC;

C. ΔKMC;

D. ΔKGC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

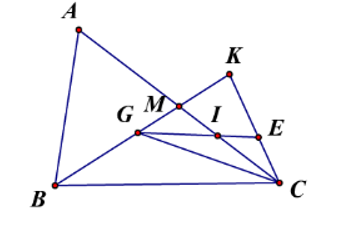
Cho tam giác ABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho (ảnh 1)

Ta có $B G = \frac{2}{3} B M$ suy ra BG = 2GM.

Khi đó GK = BG = 2GM.

Suy ra M là trung điểm của GK.

Do đó I là giao điểm ba đường trung tuyến của ΔKGC.

Vậy I là trọng tâm của ΔKGC.

Câu 3:

Cho tam giác ABC, trên đường trung tuyến AD. Gọi G là điểm nằm giữa A và D sao cho $\frac{A G}{A D} = \frac{2}{3} .$ Tia BG cắt AC tại E, tia CG cắt AB tại F. Khẳng định nào sau đây sai?

A. $\frac{B G}{E G} = 2;$

B. $\frac{F G}{C G} = \frac{2}{3};$

C. E là trung điểm của cạnh AC;

D. F là trung điểm của cạnh AB.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

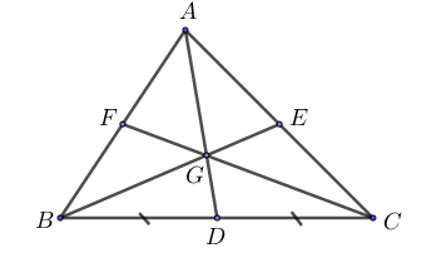
Cho tam giác ABC, trên đường trung tuyến AD. Gọi G là điểm nằm giữa A và D sao cho (ảnh 1)

Do AD là đường trung tuyến của tam giác ABC mà $\frac{A G}{A D} = \frac{2}{3}$

Suy ra G là trọng tâm của tam giác ABC.

Mặt khác, BG cắt AC tại E, CG cắt AB tại F.

Suy ra BE, CF lần lượt là hai đường trung tuyến của ΔABC.

Do đó E, F lần lượt là trung điểm của cạnh AC, AB.

Theo tính chất của ba đường trung tuyến ta có:

$\frac{B G}{B E} = \frac{2}{3}$ suy ra $\frac{B G}{E G} = 2$ ;

$\frac{C G}{C F} = \frac{2}{3}$ suy ra $\frac{C G}{F G} = 2.$ Do đó $\frac{F G}{C G} = \frac{1}{2}$ .

Vậy khẳng định ở phương án B là sai. Ta chọn phương án B.

Câu 4:

Cho hình vẽ như bên dưới. Biết AM = 12 cm.

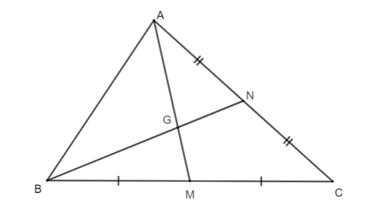
Độ dài của đoạn thẳng AG là

A. 10 cm;

B. 4 cm;

C. 6 cm;

D. 8 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{A G}{A M} = \frac{2}{3}$ (tính chất trọng tâm của tam giác)

Do đó: $A G = \frac{2}{3} A M = \frac{2}{3} .15 = 10$ (cm).

Câu 5:

Cho ∆ABC, điểm M thuộc cạnh BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là

A. Trọng tâm của ΔABD;

B. Trọng tâm của ΔABC;

C. Trọng tâm của ΔABE;

D. Cách đều ba đỉnh của ΔABD.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

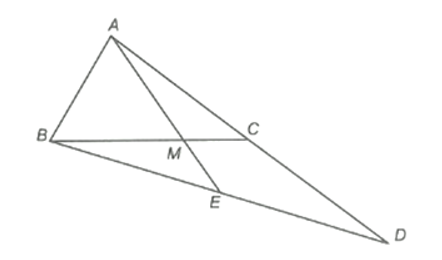
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm (ảnh 1)

Xét ΔABD có AC = CD nên C là trung điểm của AD

Do đó BC là đường trung tuyến của ΔABD.

Mà BM = 2MC nên $B M = \frac{2}{3} B C$ .

Ta có M nằm trên đường trung tuyến BC và thỏa mãn $B M = \frac{2}{3} B C$ nên M là trọng tâm của ΔABD.

Câu 6:

Cho ΔABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF. Gọi G là trọng tâm tam giác ABC. Tia AG cắt BC tại M. Khẳng định nào sau đây là đúng?

A. Hai tam giác ABC và AEF có cùng trọng tâm;

B. Hai tam giác ABC và AEC có cùng trọng tâm;

C. Hai tam giác ABC và ABF có cùng trọng tâm;

D. Hai tam giác AEM và AMF có cùng trọng tâm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

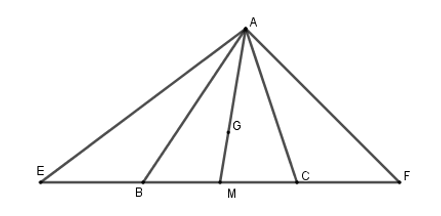
Cho tam giác ABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF (ảnh 1)

Ta có: G là trọng tâm của tam giác ABC nên AG là trung tuyến của tam giác

Mà AG cắt BC tại M nên M là trung điểm của BC

Do đó MB = MC.

Lại có BE = CF (giả thiết)

Nên MB + BE = MC + CF hay ME = MF.

Suy ra AM là đường trung tuyến ứng với cạnh EF của ΔAEF.

Mặt khác $A G = \frac{2}{3} A M$ (do G là trọng tâm của ΔABC).

Do đó G là trọng tâm của ΔAEF

Mà G là trọng tâm của ΔABC, nên hai tam giác ABC và AEF có cùng trọng tâm là điểm G.

Vậy ta chọn phương án A.

Câu 7:

Cho ΔABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho $B G = \frac{2}{3} B M$ và G là trung điểm của BK. Gọi E là trung điểm CK; GE cắt AC tại I. Số thích hợp để điền vào chỗ trống CI = … AC là:

A. $\frac{2}{3};$

B. $\frac{1}{3};$

C. $\frac{1}{2};$

D. 2.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

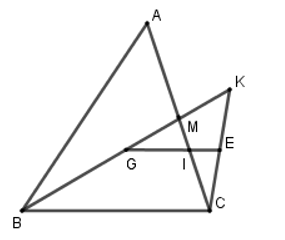
Cho tam giác ABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho BG = 2/.3 BM (ảnh 1)

Ta có $B G = \frac{2}{3} B M$ nên BG = 2GM suy ra GK = BG = 2GM.

Khi đó M là trung điểm của GK.

Do đó I là giao điểm hai đường trung tuyến CM và GE của ΔKGC.

Suy ra I là trọng tâm của ΔKGC.

Nên $C I = \frac{2}{3} C M = \frac{2}{3} . \frac{1}{2} A C = \frac{1}{3} A C$

Vậy ta chọn phương án B.

Câu 8:

Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Gọi M, N lần lượt là trung điểm của BC, CD. Đoạn thẳng AM, AN cắt BD lần lượt tại I và K. Khẳng định nào sau đây là đúng?

A. BI > IK = KD;

B. BI = IK = KD;

C. BI = IK < KD;

D. BI > IK > KD.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

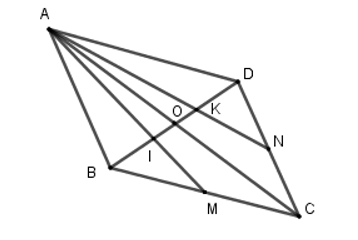
Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Gọi M, N lần lượt là trung (ảnh 1)

Ta có: ΔABC có hai đường trung tuyến BO, AM cắt nhau tại I nên I là trọng tâm của ΔABC.

Suy ra $B I = \frac{2}{3} B O$ (tính chất trọng tâm của tam giác)

Ta có: ΔADC có hai đường trung tuyến DO, AN cắt nhau tại K nên K là trọng tâm của ΔABC.

Suy ra $D K = \frac{2}{3} D O$ (tính chất trọng tâm của tam giác)

Mặt khác BO = DO (do O là trung điểm của BD)

Do đó: $B I = D K = \frac{2}{3} D O = \frac{2}{3} \cdot \frac{1}{2} B D = \frac{1}{3} B D$

Suy ra $I K = B D - B I - D K = B D - \frac{1}{3} B D - \frac{1}{3} B D = \frac{1}{3} B D .$

Khi đó BI = IK = KD.

Câu 9:

Cho tam giác ABC. Vẽ tia Bx // AC (sao cho

\hat{x B A}

và

\hat{B A C}

là một cặp góc so le trong).Lấy điểm D ∈ Bx và điểm E thuộc tia đối của tia CA sao cho BD = CE. Hai tam giác nào sau đây có cùng trọng tâm?

A. ΔABC và ΔABE;

B. ΔABE và ΔADE;

C. ΔAME và ΔABE;

D. ΔABC và ΔADE.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

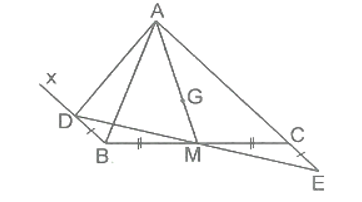
Cho tam giác ABC. Vẽ tia Bx song song AC (sao cho góc xBA và góc BAC là một cặp góc so le trong). (ảnh 1)

Gọi M là trung điểm của BC. Suy ra MB = MC.

Xét ΔBMD và ΔCME có:

BD = CE (giả thiết);

$\hat{C B x} = \hat{B C E}$ (cặp góc so le trong của Bx // AC);

MB = MC

Do đó ΔBMD = ΔCME (c.g.c).

Suy ra MD = ME (hai cạnh tương ứng) và $\hat{B M D} = \hat{C M E}$ (hai góc tương ứng)

Ta có $\hat{B M E} + \hat{C M E} = 180 °$ (kề bù).

Do đó $\hat{B M E} + \hat{B M D} = 180 °$ suy ra D, M, E thẳng hàng.

Ta có ba điểm D, M, E thẳng hàng và MD = ME nên M là trung điểm của DE.

Khi đó ΔABC và ΔADE chung đỉnh A, chung đường trung tuyến AM nên trọng tâm G của hai tam giác này trùng nhau.

Câu 10:

Cho ∆ABC có AD, BE, CF là ba đường trung tuyến cắt nhau tại G. Cho các phát biểu sau:

(I) $A D + B E + C F > \frac{3}{4} (A B + B C + A C);$

(II) AD + BE + CF < AB + BC + AC.

Chọn khẳng định đúng:

A. Chỉ (I) đúng;

B. Chỉ (II) đúng;

C. Cả (I) và (II) đều đúng;

D. Cả (I) và (II) đều sai.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Cho ∆ABC có AD, BE, CF là ba đường trung tuyến cắt nhau tại G. Cho các phát biểu sau: (ảnh 1)

• Ta xét (I):

Xét ∆ABC có AD, BE, CF là ba đường trung tuyến cắt nhau tại G nên G là trọng tâm của ∆ABC, do đó $G B = \frac{2}{3} B E$ và $G C = \frac{2}{3} C F .$

∆GBC có GB + GC > BC (bất đẳng thức tam giác).

Suy ra $\frac{2}{3} B E + \frac{2}{3} C F > B C$

Hay $\frac{2}{3} (B E + C F) > B C$

Do đó $B E + C F > \frac{3}{2} B C$ (1).

Chứng minh tương tự ta được:

⦁ $A D + B E > \frac{3}{2} A B$ (2).

⦁ $A D + C F > \frac{3}{2} A C$ (3).

Lấy (1) + (2) + (3) vế theo vế, ta được:

$2 A D + 2 B E + 2 C F > \frac{3}{2} A B + \frac{3}{2} B C + \frac{3}{2} A C$

Suy ra $2 (A D + B E + C F) > \frac{3}{2} (A B + B C + A C)$

Do đó $A D + B E + C F > \frac{3}{4} (A B + B C + A C) .$

Vậy (I) đúng.

• Ta xét (II):

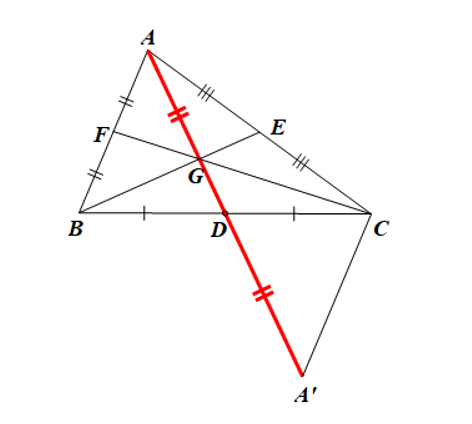
Trên tia AD, lấy điểm A’ sao cho DA’ = DA.

Xét ∆ADB và ∆A’DC, có:

DA = DA’ (theo cách dựng);

$\hat{A D B} = \hat{A^{'} D C}$ (hai góc đối đỉnh);

BD = CD (do AD là đường trung tuyến của ∆ABC)

Do đó ∆ADB = ∆A’DC (c.g.c).

Suy ra AB = A’C (hai cạnh tương ứng).

Áp dụng bất đẳng thức tam giác cho ∆AA’C, ta được: AA’ < AC + A’C.

Suy ra AA’ < AC + AB hay 2AD < AC + AB (4).

Chứng minh tương tự, ta được:

⦁ 2BE < AB + BC (5).

⦁ 2CF < AC + BC (6).

Lấy (4) + (5) + (6) vế theo vế, ta được:

2AD + 2BE + 2CF < 2AC + 2AB + 2BC.

Suy ra 2(AD + BE + CF) < 2(AB + AC + BC).

Do đó AD + BE + CF < AB + AC + BC.

Vậy (II) đúng.

Kết luận: cả (I) và (II) đều đúng.

Ta chọn phương án C.

Trắc nghiệm Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án

Dạng 2. Chứng minh một điểm là trọng tâm của tam giác

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương