Trắc nghiệm Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án
Dạng 4. Nhận biết đường phân giác và đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
-
541 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho điểm E nằm trên tia phân giác góc A của tam giác ABC. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Điểm E nằm trên tia phân giác góc A của tam giác ABC thì E cách đều hai cạnh AB, AC.
Câu 2:
Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Hai đường phân giác CD và BE cắt nhau tại I mà nên I là giao điểm của ba đường phân giác của ∆ABC, do đó AI là phân giác của góc A.
Câu 3:
Em hãy điền cụm từ thích hợp nhất vào chỗ trống:
"Ba đường phân giác của tam giác giao nhau tại 1 điểm. Điểm này cách đều ... của tam giác đó".
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác.
Câu 4:
Cho ΔABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
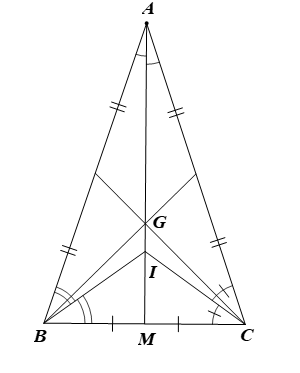
⦁ I là giao điểm của các đường phân giác trong tam giác nên I cách đều ba cạnh của ΔABC. Do đó khẳng định A là sai.
⦁ G là trọng tâm nên G là giao điểm của ba đường trung tuyến, không phải giao điểm ba đường phân giác của tam giác, hay G khác I, do đó khẳng định C là sai.
⦁ Ta có: ΔABC cân tại A, I là giao điểm của các đường phân giác trong tam giác nên AI vừa là đường trung tuyến đồng thời là đường phân giác của Mà G là trọng tâm của ΔABC nên AG là trung tuyến của ΔABC.
Do đó AI và AG là hai đường thẳng trùng nhau hay A, G, I thẳng hàng.
Vậy khẳng định B là đúng, ta chọn phương án B.
Câu 5:
Cho ΔABC có trọng tâm G và I là giao của ba đường phân giác của tam giác ΔABC. Biết B; G; I thẳng hàng. Khi đó ΔABC là tam giác gì?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
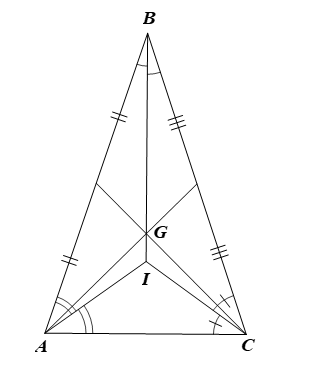
⦁ Vì I là giao của ba đường phân giác của ΔABC nên BI là đường phân giác của ΔABC.
⦁ Vì G là trọng tâm ΔABC nên BG là đường trung tuyến của ΔABC mà B; I; G thẳng hàng nên ta có BI là đường trung tuyến của ΔABC.
Xét ΔABC có: BI là đường trung tuyến đồng thời là đường phân giác của ΔABC.
Suy ra ΔABC cân tại B.
Câu 6:
Cho ΔABC có các tia phân giác của và cắt nhau tại I. Gọi D, E là chân các đường vuông góc hạ từ I đến các cạnh AB và AC. Khi đó ta có:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
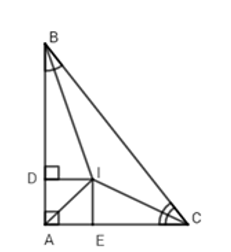
Xét ΔABC có các tia phân giác của và cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔABC.
Suy ra AI là đường phân giác của và I cách đều ba cạnh của ΔABC, do đó ID = IE.
Vậy ta chọn phương án D.
Câu 7:
Cho tam giác ABC cân tại A có đường phân giác AD (D nằm trong tam giác ABC).
Biết CD = 5 cm. Độ dài đoạn BD là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
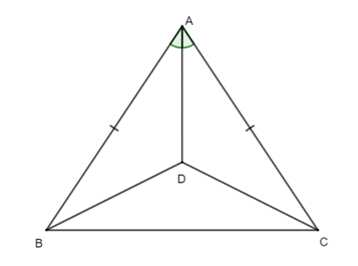
Xét ∆ABD và ∆ACD có:
AD là cạnh chung;
(do AD là tia phân giác của góc BAC);
AB = AC (do ∆ABC cân tại A).
Do đó ∆ABD = ∆ACD (c.g.c).
Suy ra BD = CD = 5 (cm) (hai cạnh tương ứng).
Câu 10:
Cho tam giác ABC đều có hai đường phân giác của góc B và C cắt nhau tại I. Gọi M là trung điểm của BC. Biết AI = 3 cm, độ dài đoạn thẳng IM là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
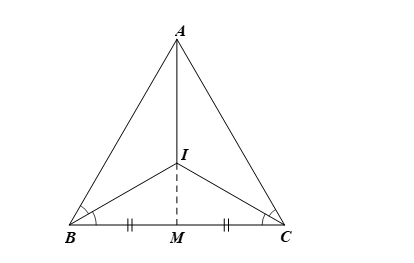
Xét ∆ABC đều có BI, CI là hai đường phân giác của tam giác nên AI cũng là đường phân giác của góc
Do đó AI cũng đồng thời là đường trung tuyến của ∆ABC.
Chứng minh tương tự, ta sẽ có BI, CI đều là đường trung tuyến của ∆ABC.
Suy ra I là trọng tâm của ∆ABC
Khi đó A, I, M thẳng hàng và
Suy ra