10 câu hỏi trắc nghiệm thuộc Dạng 3: Xác định và tính góc giữa đường thẳng và mặt phẳng có đáp án

Trắc nghiệm Toán 11 Bài 24. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng có đáp án

Dạng 3: Xác định và tính góc giữa đường thẳng và mặt phẳng có đáp án

265 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình chóp S.ABC, có SA ⊥ (ABC). Góc giữa đường thẳng SC và mặt đáy là góc nào dưới đây?

A. $\hat{S A C}$

B. $\hat{S B C}$

C. $\hat{S C A}$

D. $\hat{C S A}$

Xem đáp án

Đáp án đúng là: C

Cho hình chóp S.ABC, có SA ⊥ (ABC). Góc giữa đường thẳng SC và mặt đáy là góc nào dưới đây? (ảnh 1)

Ta có: SC ∩ (ABC) = C.

Hình chiếu vuông góc của S lên (ABC) là A.

Do đó, ta có: $(S C, (A B C)) = (S C, A C) = \hat{S C A}$ .

Câu 2:

Cho hình chóp S.ABC, có SA ⊥ (ABC). Góc giữa đường thẳng SB và đáy là góc nào dưới đây?

A. $\hat{S B A}$

B. $\hat{S B C}$

C. $\hat{S C A}$

D. $\hat{C S A}$

Xem đáp án

Đáp án đúng là: A

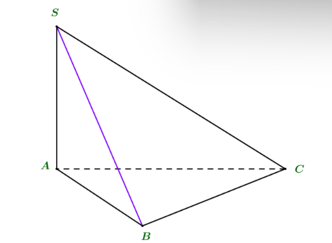
Cho hình chóp S.ABC, có SA ⊥ (ABC). Góc giữa đường thẳng SB và đáy là góc nào dưới đây? (ảnh 1)

Ta có: SB ∩ (ABC) = B

Hình chiếu vuông góc của S lên (ABC) là A.

Do đó, ta có: $(S B, (A B C)) = (S B, A B) = \hat{S B A}$ .

Câu 3:

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA ⊥ (ABC). Góc giữa đường thẳng SC và mặt phẳng (SAB) là góc nào dưới đây?

A. $\hat{S C A}$

B. $\hat{S B C}$

C. $\hat{B S C}$

D. $\hat{S C B}$

Xem đáp án

Đáp án đúng là: C

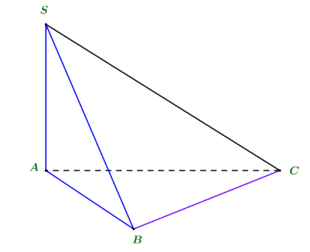
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA ⊥ (ABC). Góc giữa đường thẳng SC và mặt phẳng (SAB) là góc nào dưới đây? (ảnh 1)

Ta có:

BC ⊥ AB (tam giác ABC vuông tại B)

BC ⊥ SA (SA ⊥ (ABC))

Suy ra: BC ⊥ (SAB).

Khi đó hình chiếu vuông góc của C lên (SAB) là B.

SC ∩ (SAB) = S

Vậy $(S C, (S A B)) = (S C, S B) = \hat{B S C}$ .

Câu 4:

Cho hình lập phương ABCD.A'B'C'D'. Xác định góc giữa đường thẳng A'C và mặt phẳng (ABCD).

A. $\hat{A' C A}$

B. $\hat{A A' C}$

C. $\hat{A' C B}$

D. $\hat{A' C D'}$

Xem đáp án

Đáp án đúng là: A

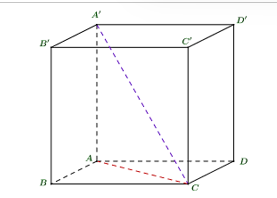
Cho hình lập phương ABCD.A'B'C'D'. Xác định góc giữa đường thẳng A'C và mặt phẳng (ABCD). (ảnh 1)

Hình chiếu vuông góc của A' lên (ABCD) là A

A'C ∩ (ABCD) = C

Suy ra: $(A' C, (A B C D)) = (A' C, A C) = \hat{A' C A}$ .

Câu 5:

Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = $\sqrt{3}$ và AA' = 1. Góc tạo bởi đường thẳng AC' và (ABC) bằng:

A. $60 °$

B. 30 $°$

C. 90 $°$

D. 45 $°$

Xem đáp án

Đáp án đúng là: B

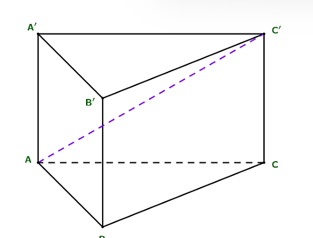
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = c ăn 3 và AA' = 1. Góc tạo bởi đường thẳng AC' và (ABC) bằng: (ảnh 1)

Hình chiếu vuông góc của C' lên (ABC) là C

AC' ∩ (ABC) = A

Suy ra: $(A C', (A B C)) = (A C', A C) = \hat{C' A C}$ .

Vì ABC.A'B'C' là hình lăng trụ tam giác đều nên AC = AB = $\sqrt{3}$ , CC' = AA' = 1.

Xét tam giác ACC' vuông tại C có:

$\tan \hat{C' A C} = \frac{C C'}{A C} = \frac{1}{\sqrt{3}} \Rightarrow \hat{C' A C} = 30 °$ .

Câu 6:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = 2 và AA' = 2 $\sqrt{2}$ . Góc giữa đường thẳng CA' và mặt phẳng (ABCD) bằng:

A. $30 °$

B. $60 °$

C. $90 °$

D. $45 °$

Xem đáp án

Đáp án đúng là: D

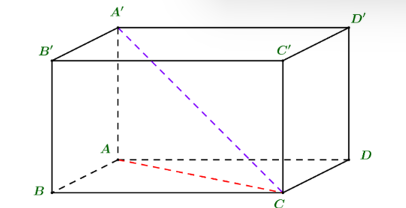
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = 2 và (ảnh 1)

Hình chiếu vuông góc của A' lên (ABCD) là A

A'C ∩ (ABCD) = C

Suy ra: $(A' C, (A B C D)) = (A' C, A C) = \hat{A' C A}$

Áp dụng định lí Pythagore cho tam giác vuông ABC ta có:

AC² = AB² + BC² = 2² + 2² = 8 $\Rightarrow A C = 2 \sqrt{2}$

Xét tam giác vuông ACA' có:

$\tan \hat{A C A'} = \frac{A A'}{A C} = \frac{2 \sqrt{2}}{2 \sqrt{2}} = 1 \Rightarrow \hat{A C A'} = 45 °$

Câu 7:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính côsin góc giữa đường thẳng A'C và mặt phẳng (ABB'A').

A. $\frac{\sqrt{3}}{3}$

B. $\frac{\sqrt{6}}{3}$

C. $\sqrt{2}$

D. $\frac{\sqrt{2}}{2}$

Xem đáp án

Đáp án đúng là: B

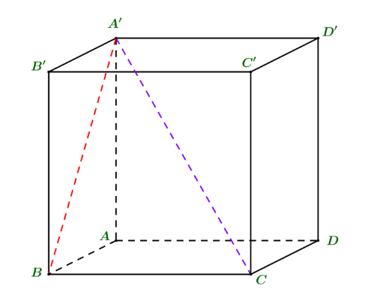
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính côsin góc giữa đường thẳng A'C và mặt phẳng (ABB'A'). (ảnh 1)

Ta có:

BC ⊥ AB (do ABCD là hình vuông)

BC ⊥ AA' (do AA' ⊥ (ABCD))

Suy ra: BC ⊥ (ABB'A').

Hình chiếu vuông góc của C lên (ABB'A') là B

Mà A'C ∩ (ABB'A') = A'.

Do đó, ta có: $(A' C, (A B B' A')) = (A' C, A' B) = \hat{B A' C}$

Áp dụng định lí Pythagore cho tam giác vuông ABA' ta có:

A'B² = AB² + AA'² = 1² + 1² = 2

$\Rightarrow A' B = \sqrt{2}$

Tương tự, ta tính được AC = $\sqrt{2}$ .

Từ đó suy ra A'C = $\sqrt{3}$ (định lí Pythagore trong tam giác vuông A'AC).

Xét tam giác A'BC vuông tại B có:

$\cos \hat{B A' C} = \frac{A' B}{A' C} = \frac{\sqrt{2}}{\sqrt{3}} = \frac{\sqrt{6}}{3}$ .

Vậy côsin góc giữa đường thẳng A'C và mặt phẳng (ABB'A') bằng $\frac{\sqrt{6}}{3}$ .

Câu 8:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2 và cạnh bên bằng 2 $\sqrt{2}$ . Khi đó góc giữa cạnh bên và mặt đáy bằng

A. 30 $°$

B. 45 $°$

C. 60 $°$

D. 90 $°$

Xem đáp án

Đáp án đúng là: C

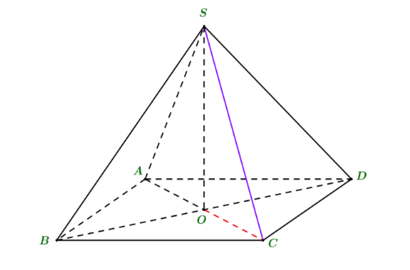
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2 và cạnh bên bằng 2căn 2. Khi đó góc giữa cạnh bên và mặt đáy bằng (ảnh 1)

Gọi O là giao điểm của AC và BD, ta có: SO ⊥ (ABCD).

Chọn cạnh bên SA.

SA ∩ (ABCD) = A và O là hình chiếu vuông góc của S lên (ABCD) nên:

$(S A, (A B C D)) = (S A, O A) = \hat{S A O}$

Ta có: $A O = \frac{1}{2} A C = \frac{1}{2} \sqrt{A B^{2} + B C^{2}} = \frac{1}{2} \sqrt{2^{2} + 2^{2}} = \sqrt{2}$

\Rightarrow \cos \hat{S A O} = \frac{O A}{S A} = \frac{\sqrt{2}}{2 \sqrt{2}} = \frac{1}{2} \Rightarrow \hat{S A O} = 60 °

Câu 9:

Cho hình lập phương ABCD.A'B'C'D'. Tính côsin góc giữa đường thẳng BD' và mặt phẳng đáy bằng bao nhiêu?

A. $\frac{\sqrt{3}}{3}$

B. $\frac{\sqrt{6}}{3}$

C. $\sqrt{2}$

D. $\frac{\sqrt{2}}{2}$

Xem đáp án

Đáp án đúng là: B

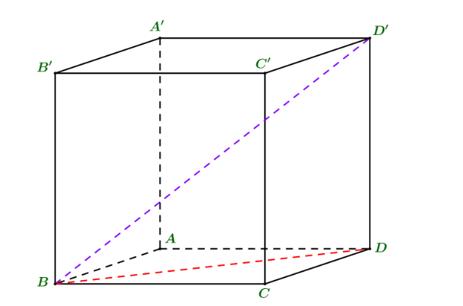
Cho hình lập phương ABCD.A'B'C'D'. Tính côsin góc giữa đường thẳng BD' và mặt phẳng đáy bằng bao nhiêu? (ảnh 1)

Giả sử cạnh của hình lập phương là 1.

Hình chiếu vuông góc của BD' lên đáy (ABCD) là BD nên: $(B D', (A B C D)) = (B D', B D) = \hat{D B D'}$

Áp dụng định lý Pythagore cho tam giác vuông BCD ta có:

BD² = BC² + CD² = 1² + 1² = 2 $\Rightarrow B D = \sqrt{2}$

Áp dụng định lý Pythagore cho tam giác vuông BDD' ta có:

BD'² = BD² + D'D² = ${(\sqrt{2})}^{2}$ + 1² = 3 $\Rightarrow B D' = \sqrt{3}$

Trong tam giác vuông BDD' có:

$\cos \hat{D B D'} = \frac{B D}{B D'} = \frac{\sqrt{2}}{\sqrt{3}} = \frac{\sqrt{6}}{3}$ .

Câu 10:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, biết SA ⊥ (ABCD) và SA = $a \sqrt{6}$ . Gọi M là trung điểm của SB. Tính góc giữa đường thẳng BM và (ABCD).

A. 30 $°$

B. $45 °$

C. $60 °$

D. $90 °$

Xem đáp án

Đáp án đúng là: C

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, biết SA ⊥ (ABCD) (ảnh 1)

Gọi O là tâm của đáy ABCD.

Vì MO // SA (sử dụng tính chất đường trung bình)

Mà SA ⊥ (ABCD) nên MO ⊥ (ABCD)

Hình chiếu vuông góc của M lên (ABCD) là O

BM ∩ (ABCD) = B

Do đó: $(B M, (A B C D)) = (B M, B O) = \hat{M B O}$ .

MO là đường trung bình của tam giác SAC nên: $M O = \frac{1}{2} S A = \frac{a \sqrt{6}}{2}$ .

Ta có: $B O = \frac{1}{2} B D = \frac{a \sqrt{2}}{2}$ .

Trong tam giác vuông BMO có:

$\tan \hat{M B O} = \frac{M O}{B O} = \frac{\frac{a \sqrt{6}}{2}}{\frac{a \sqrt{2}}{2}} = \sqrt{3} \Rightarrow \hat{B M O} = 60 °$ .

Vậy góc giữa đường thẳng BM và (ABCD) bằng 60°.

Bắt đầu thi ngay

Trắc nghiệm Toán 11 Bài 24. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng có đáp án

Dạng 3: Xác định và tính góc giữa đường thẳng và mặt phẳng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương