Trắc nghiệm Toán 11 Bài 24. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng có đáp án
Dạng 2: Vận dụng định lí ba đường vuông góc để chứng minh hai đường thẳng vuông góc có đáp án
-
247 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: A
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). Khi đó, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a' của a trên (P).
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Đường thẳng SB vuông góc với đường thẳng nào sau đây?
Xem đáp án
Đáp án đúng là: A
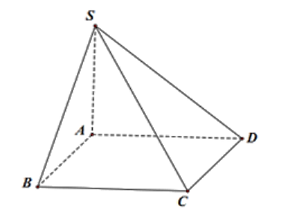
Do SA ⊥ (ABCD) nên hình chiếu vuông góc của S lên (ABCD) là A.
Do đó, hình chiếu vuông góc của SB lên (ABCD) là AB.
Do ABCD là hình vuông nên AB ⊥ AD.
Suy ra: SB ⊥ AD (định lí ba đường vuông góc).
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, H là tâm hình vuông ABCD, SH ⊥ (ABCD). Đường thẳng SA vuông góc với đường thẳng nào sau đây?
Xem đáp án
Đáp án đúng là: B
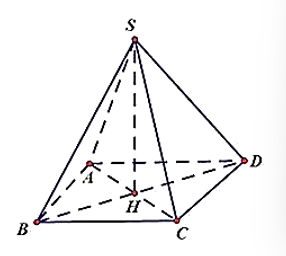
Vì SH ⊥ (ABCD) nên hình chiếu vuông góc của SA lên (ABCD) là AH
Vì ABCD là hình vuông, H là tâm hình vuông ABCD nên AH vuông góc với BD
Do đó, SA vuông góc với BD (định lí ba đường vuông góc).
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: A
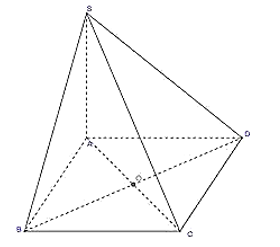
Do SA ⊥ (ABCD) nên hình chiếu vuông góc của S lên (ABCD) là A.
Do đó, hình chiếu vuông góc của SD lên (ABCD) là AD.
Do ABCD là hình vuông nên CD ⊥ AD.
Suy ra: SD ⊥ CD (định lí ba đường vuông góc).
Do đó, tam giác SCD vuông tại D.
Câu 5:
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Kẻ AH ⊥ SB tại H, AK ⊥ SB tại K. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng là: D
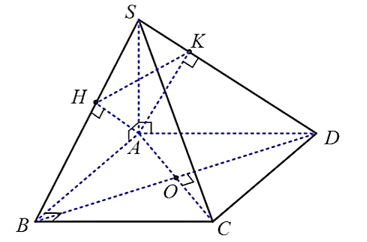
Do SA ⊥ (ABCD) nên hình chiếu vuông góc của S lên (ABCD) là A, do đó, hình chiếu vuông góc của SC lên (ABCD) là AC.
Mà do ABCD là hình vuông nên AC ⊥ BD
Theo định lí ba đường vuông góc, ta có: SC ⊥ BD
Do SA ⊥ (ABCD) nên hình chiếu vuông góc của S lên (ABCD) là A, do đó, hình chiếu vuông góc của SB lên (ABCD) là AB.
Mà do ABCD là hình vuông nên AB ⊥ BC
Theo định lí ba đường vuông góc, ta có: SB ⊥ BC
Do SA ⊥ (ABCD) nên hình chiếu vuông góc của S lên (ABCD) là A, do đó, hình chiếu vuông góc của SD lên (ABCD) là AD.
Mà do ABCD là hình vuông nên AD ⊥ CD
Theo định lí ba đường vuông góc, ta có: SD ⊥ CD
Vậy các đáp án A, B, C đúng nên D sai.
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = a. SA vuông góc với đáy. Gọi M là trung điểm của AD. Đường thẳng BM vuông góc với đường thẳng:
Xem đáp án
Đáp án đúng là: A
Câu 7:
Hình chóp tam giác đều S.ABC có cạnh bên bằng cạnh đáy. Đường thẳng SA vuông góc với đường thẳng nào sau đây?
Xem đáp án
Đáp án đúng là: A
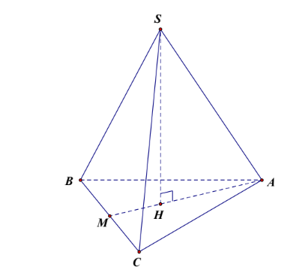
Hình chóp S.ABC có tất cả các cạnh đều bằng nhau nên là hình tứ diện đều.
Khi đó, hình chiếu vuông góc của S lên (ABC) là tâm đường tròn ngoại tiếp tam giác ABC và chính là trọng tâm H của tam giác ABC.
Do đó, H thuộc đường trung tuyến AM của tam giác ABC, mà ABC là tam giác đều nên AH cũng là đường cao, do đó, AH ⊥ BC.
Hình chiếu vuông góc của SA lên (ABC) là AH.
Suy ra: SA ⊥ BC.
Câu 8:
Cho hình chóp S.MNPQ, MNPQ là hình chữ nhật, trung điểm A của MN là hình chiếu vuông góc của S lên đáy, B là trung điểm của QP. Đường thẳng SN vuông góc với đường thẳng nào dưới đây?
Xem đáp án
Đáp án đúng là: D
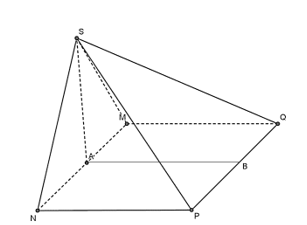
Ta có hình chiếu vuông góc của S lên (MNPQ) là A.
Vì N thuộc (MNPQ) nên hình chiếu vuông góc của N lên (MNPQ) là N.
Do đó, hình chiếu vuông góc của SN lên (MNPQ) là AN.
Vì A là trung điểm của MN, B là trung điểm của QP và MNPQ là hình chữ nhật.
Nên AB // MQ // NP.
Mà AN vuông góc với NP.
Suy ra: AB vuông góc với AN.
Theo định lí ba đường vuông góc, ta có: SN vuông góc với AB.
Câu 9:
Cho hình chóp S.MNPQ, MNPQ là vuông, A là trung điểm của MN, B là trung điểm của QP, C là trung điểm của MQ, D là trung điểm của NP. Đường thẳng SC vuông góc với đường thẳng nào dưới đây?
Xem đáp án
Đáp án đúng là: A
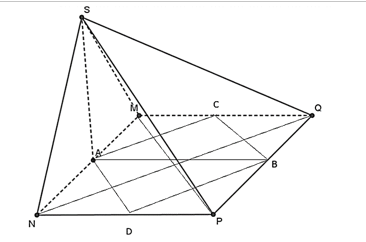
Vì SA vuông góc với đáy nên hình chiếu vuông góc của S lên (MNPQ) là A.
Vì C thuộc (MNPQ) nên hình chiếu vuông góc của C lên (MNPQ) là C.
Do đó, hình chiếu vuông góc của SC lên (MNPQ) là AC.
Vì MNPQ là hình vuông nên:
MP ⊥ NQ, MP = NQ
Vì A, B, C, D lần lượt là trung điểm của của MN, PQ, MQ, NP
Do đó, ACBD là hình vuông.
Suy ra: AC ⊥ CB
Vậy SC ⊥ CB (theo định lí ba đường vuông góc).
Câu 10:
Hình chóp tam giác đều S.ABC có cạnh bên bằng cạnh đáy, K là trung điểm của AB. Khẳng định nào sau đây sai?
Xem đáp án
Đáp án đúng là: D
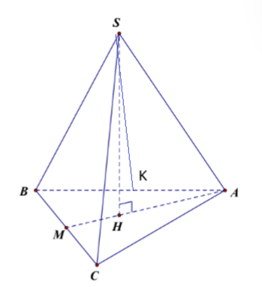
Đáp án D sai vì AK không là hình chiếu vuông góc của SA lên (ABC).