Dạng 2: Tìm giới hạn của dãy số dựa vào các định lý và các giới hạn cơ bản có đáp án
-
158 lượt thi
-
84 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho dãy số (un) với 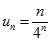 và
và 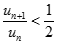 . Chọn giá trị đúng của
. Chọn giá trị đúng của 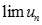 trong các số sau:
trong các số sau:
 Xem đáp án
Xem đáp án
Chọn C.
Chứng minh bằng phương pháp quy nạp toán học ta có 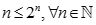
Nên ta có : 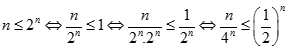
Suy ra : 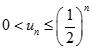 , mà
, mà 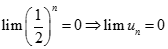
Câu 23:
Giá trị của 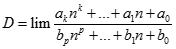 (Trong đó k, p là các số nguyên dương;
(Trong đó k, p là các số nguyên dương; 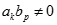 ).
).
 Xem đáp án
Xem đáp án
Chọn C.
Ta xét ba trường hợp sau
k > p . Chia cả tử và mẫu cho 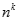 ta có
ta có 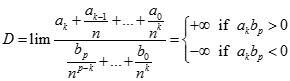 .
.
k = p. Chia cả tử và mẫu cho 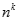 ta có:
ta có: 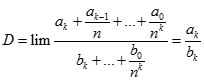 .
.
k < p. Chia cả tử và mẫu cho 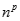 :
: 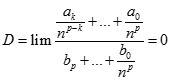 .
.
Câu 32:
Cho các số thực a,b thỏa 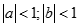 . Tìm giới hạn
. Tìm giới hạn 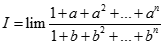 .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có 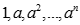 là một cấp số nhân công bội a
là một cấp số nhân công bội a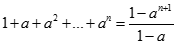
Tương tự 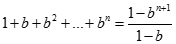
Suy ra lim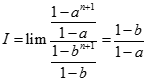
( Vì 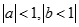
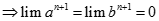 ).
).
Câu 33:
Tính giới hạn của dãy số 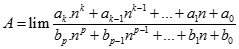 với
với 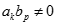 .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta chia làm các trường hợp sau
TH 1: n = k, chia cả tử và mẫu cho nk , ta được 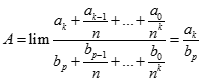
TH 2: k > p, chia cả tử và mẫu cho nk , ta được 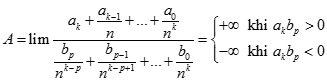
TH 3: k < p, chia cả tử và mẫu cho np , ta được 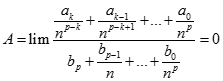
Câu 66:
Cho dãy số 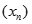 xác định bởi
xác định bởi 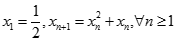
Đặt 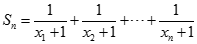 . Tính
. Tính 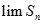
 Xem đáp án
Xem đáp án
Chọn C.
Từ công thức truy hồi ta có: 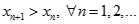
Nên dãy 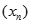 là dãy số tăng.
là dãy số tăng.
Giả sử dãy 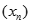 là dãy bị chặn trên, khi đó sẽ tồn tại
là dãy bị chặn trên, khi đó sẽ tồn tại 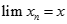
Với x là nghiệm của phương trình : 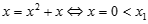 vô lí
vô lí
Do đó dãy 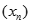 không bị chặn, hay
không bị chặn, hay 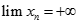
Mặt khác: 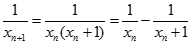
Suy ra: 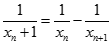
Dẫn tới: 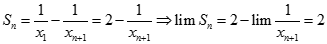
Câu 67:
Cho dãy 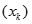 được xác định như sau:
được xác định như sau: 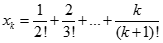
Tìm 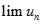 với
với 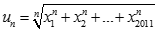 .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: 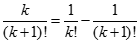 nên
nên 
Suy ra 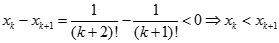
Mà: 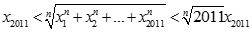
Mặt khác: 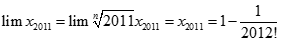
Vậy 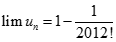 .
.
Câu 68:
Cho dãy số 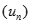 được xác định bởi:
được xác định bởi: 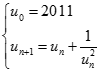 . Tìm
. Tìm 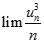 .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta thấy 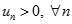
Ta có: 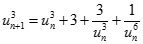 (1)
(1)
Suy ra: 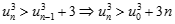 (2)
(2)
Từ (1) và (2), suy ra: 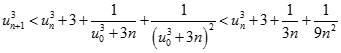
Do đó: 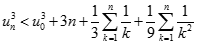 (3)
(3)
Lại có: 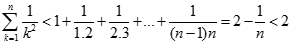
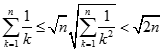
Nên: 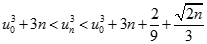
Hay 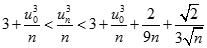
Vậy 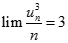
.
Câu 69:
Cho dãy x > 0 xác định như sau: 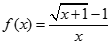 . Tìm
. Tìm 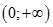 .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
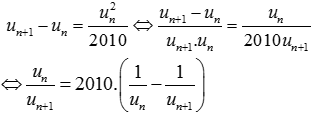
Ta có 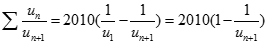
Mặt khác ta chứng minh được: 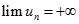 .
.
Nên 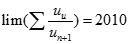
Câu 76:
Cho dãy số 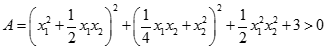 được xác định như sau
được xác định như sau 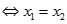 .
.
Đặt 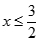 . Tìm
. Tìm 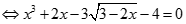 .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
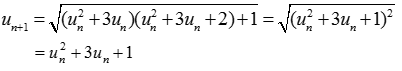
Suy ra: 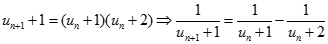
Suy ra: 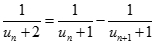
Do đó, suy ra: 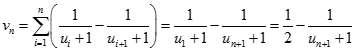
Mặt khác, từ 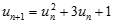 ta suy ra:
ta suy ra: 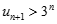 .
.
Nên 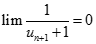 . Vậy
. Vậy 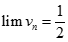 .
.
Câu 77:
Cho 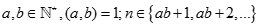 . Kí hiệu
. Kí hiệu 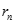 là số cặp số
là số cặp số 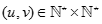
sao cho 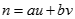 . Tìm
. Tìm 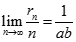
 Xem đáp án
Xem đáp án
Chọn C.
Xét phương trình 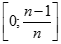 (1).
(1).
Gọi 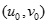 là một nghiệm nguyên dương của (1). Giả sử
là một nghiệm nguyên dương của (1). Giả sử 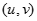 là một nghiệm nguyên dương khác
là một nghiệm nguyên dương khác 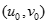 của (1).
của (1).
Ta có 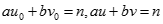 suy ra
suy ra 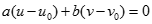 do đó tồn tại k nguyên dương sao cho
do đó tồn tại k nguyên dương sao cho 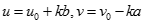 . Do v là số nguyên dương nên
. Do v là số nguyên dương nên 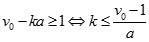 . (2)
. (2)
Ta nhận thấy số nghiệm nguyên dương của phương trình (1) bằng số các số k nguyên dương cộng với 1. Do đó 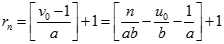 .
.
Từ đó ta thu được bất đẳng thức sau: 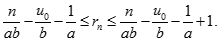
Từ đó suy ra : 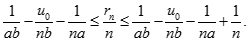
Từ đây áp dụng nguyên lý kẹp ta có ngay 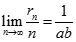 .
.
Câu 78:
Cho dãy số có giới hạn (un) xác định bởi 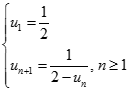 . Tìm kết quả đúng của
. Tìm kết quả đúng của 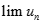 .
.
 Xem đáp án
Xem đáp án
Chọn B.
Ta có 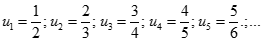
Dự đoán 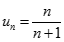 với
với 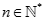
Dễ dàng chứng minh dự đoán trên bằng phương pháp quy nạp.
Từ đó 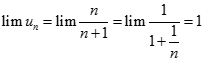
Câu 83:
Tính giới hạn: ![Tính giới hạn: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] A. 11/18 B.2 C. 1 D. 3/2 Chọn A Cách 1: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid12-1669825838.png) .
.
 Xem đáp án
Xem đáp án
Chọn A.
Cách 1:
![Tính giới hạn: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] A. 11/18 B.2 C. 1 D. 3/2 Chọn A Cách 1: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid10-1669825744.png)
Cách 2: Bấm máy tính như sau: ![Tính giới hạn: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] A. 11/18 B.2 C. 1 D. 3/2 Chọn A Cách 1: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid11-1669825753.png) và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).
và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).
Câu 84:
Tính giới hạn: ![Tính giới hạn: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] A. 1 B. 1/2 C. 1/4 D. 3/2 Chọn B. Cách 1: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid15-1669825983.png) .
.
 Xem đáp án
Xem đáp án
Chọn B.
Cách 1:
![Tính giới hạn: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] A. 1 B. 1/2 C. 1/4 D. 3/2 Chọn B. Cách 1: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid14-1669825893.png)
Cách 2: Bấm máy tính như sau: ![Tính giới hạn: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] A. 1 B. 1/2 C. 1/4 D. 3/2 Chọn B. Cách 1: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid13-1669825857.png) và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).
và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).

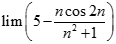
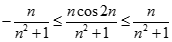
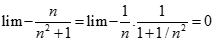
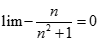
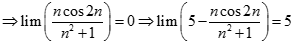
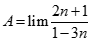
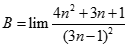
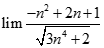
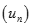
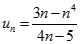
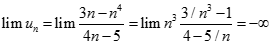
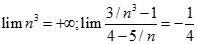
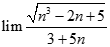
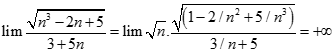
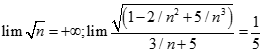
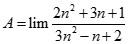
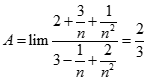
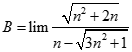
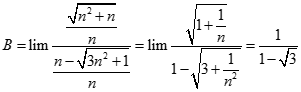
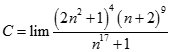
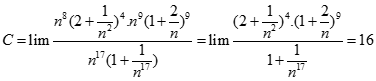
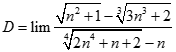
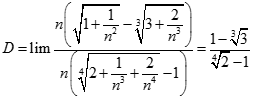
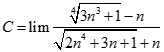
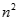
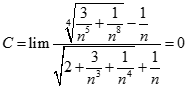
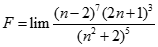
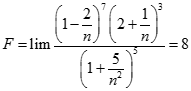
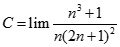
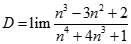
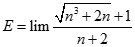
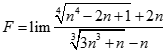
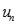
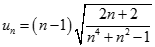 . Chọn kết quả đúng của
. Chọn kết quả đúng của 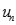
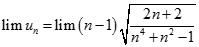
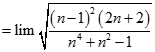
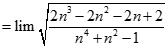

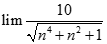 bằng:
bằng: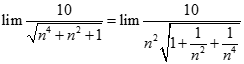
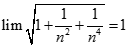
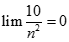
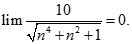
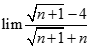
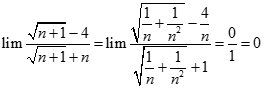
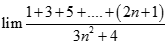
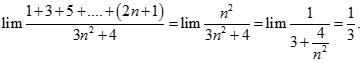
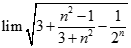
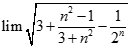
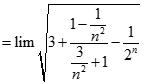
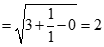
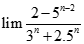
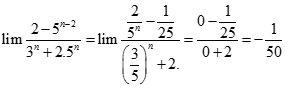
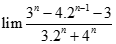 bằng:
bằng: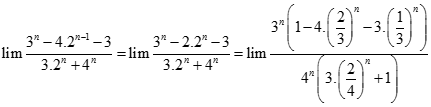
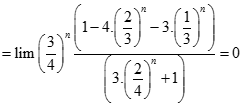
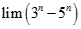
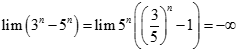
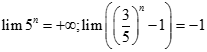
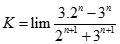
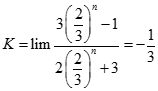
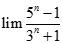 bằng:
bằng: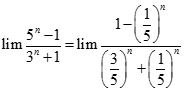
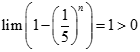
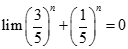
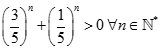
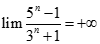
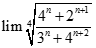 bằng:
bằng: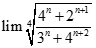
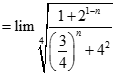
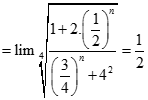
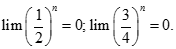
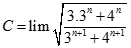
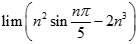 bằng:
bằng: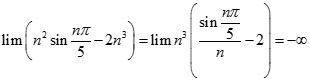
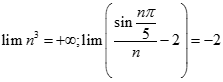
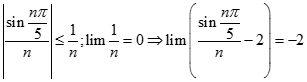
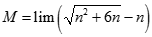
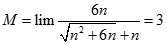
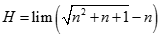
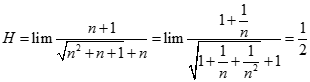
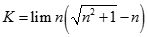
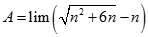
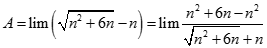
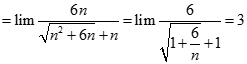
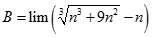
![Giá trị đúng của lim [ căn bậc hai n (căn bậc hai n + 1 - căn bậc hai n - 1)] là: A. -1 B. 0 C. 1 D. dương vô cùng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid25-1669818935.png)
![Giá trị đúng của lim [ căn bậc hai n (căn bậc hai n + 1 - căn bậc hai n - 1)] là: A. -1 B. 0 C. 1 D. dương vô cùng (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid24-1669818791.png)
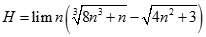
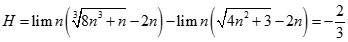
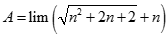
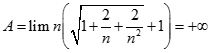
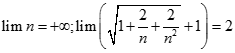
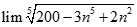 bằng:
bằng: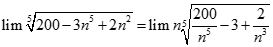
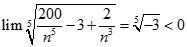
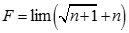
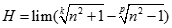
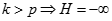
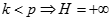
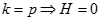
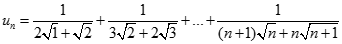
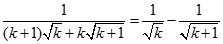
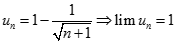
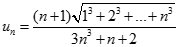
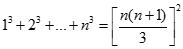
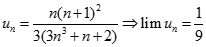
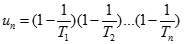
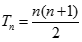
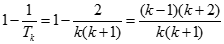
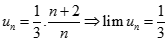
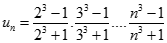
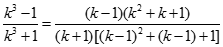
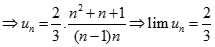
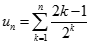
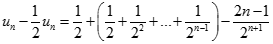
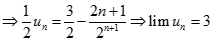
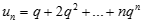
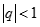
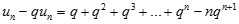
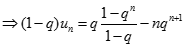
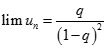
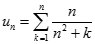
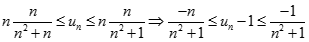
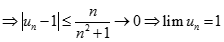
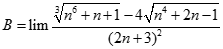
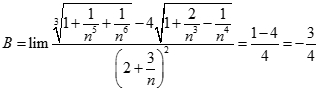
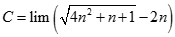
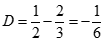
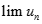
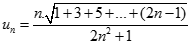
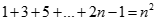
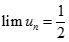
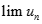
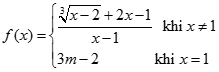
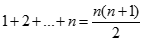
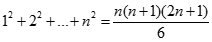
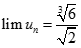
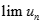
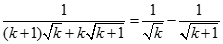
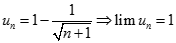
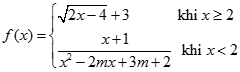
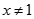
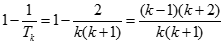
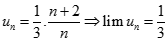
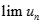
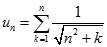
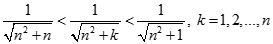
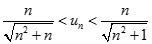
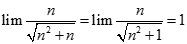
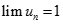
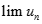
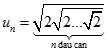
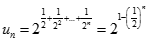

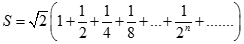
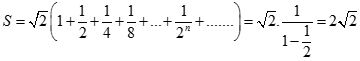
![Tính giới hạn: lim [ 1/1.2 + 1/2.3 + ... + 1/n(n+ 1)] A. 0 B. 1 C. 3/2 D. không giới hạn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid3-1669825453.png)
![Tính giới hạn: lim [ 1/1.2 + 1/2.3 + ... + 1/n(n+ 1)] A. 0 B. 1 C. 3/2 D. không giới hạn (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid2-1669825377.png)
![Tính giới hạn: lim [1/1.3 + 1/3.5 + ... + 1/n(2n+1)] A. 1 B. 0 C. 2/3 D. 2 . Chọn B Đặt A = 1/1.3 + 1/3.5 + ... + 1/n(2n+1) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid6-1669825586.png)
![Tính giới hạn: lim [1/1.3 + 1/3.5 + ... + 1/n(2n+1)] A. 1 B. 0 C. 2/3 D. 2 . Chọn B Đặt A = 1/1.3 + 1/3.5 + ... + 1/n(2n+1) (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid4-1669825481.png)
![Tính giới hạn: lim [1/1.3 + 1/3.5 + ... + 1/n(2n+1)] A. 1 B. 0 C. 2/3 D. 2 . Chọn B Đặt A = 1/1.3 + 1/3.5 + ... + 1/n(2n+1) (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid5-1669825495.png)
![Tính giới hạn: lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] A. 3/4 B. 1 C. 0 D. 2/3 Chọn A lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid9-1669825717.png)
![Tính giới hạn: lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] A. 3/4 B. 1 C. 0 D. 2/3 Chọn A lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid7-1669825625.png)
![Tính giới hạn: lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] A. 3/4 B. 1 C. 0 D. 2/3 Chọn A lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid8-1669825628.png)