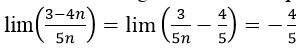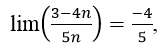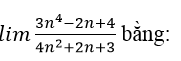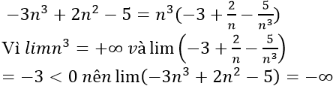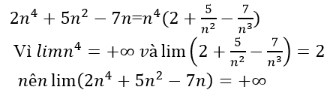33 câu hỏi trắc nghiệm thuộc Trắc nghiệm Giới hạn của dãy số có đáp án

Câu 1:

Dãy số nào sau đây có giới hạn khác 0?

A. 1/n

B. $1 / \sqrt{n}$

C. (n+1)/n

D. $(\sin n) / \sqrt{n}$

Xem đáp án

- Cách 1:

Đáp án C

- Cách 2 (phương pháp loại trừ): Từ các định lí ta thấy:

Các dãy ở phương án A,B đều bằng 0, do đó loại phương án A,B

Do đó loại phương án D. Chọn đáp án C

Câu 2:

Dãy số nào sau đây có giới hạn bằng 0?

A. ${(\frac{4}{3})}^{n}$

B. ${(\frac{- 4}{3})}^{n}$

C. ${(\frac{- 5}{3})}^{n}$

D. ${(\frac{1}{3})}^{n}$

Xem đáp án

- Cách 1: Dãy (1/3)n có giới hạn 0 vì |q| < 1 thì lim $q^{n}$ = 0. Đáp án là D

- Cách 2: Các dãy ở các phương án A,B,C đều có dạng lim $q^{n}$ nhưng |q| > 1 nên không có giới hạn 0, do đó loại phương án A,B,C.

Chọn đáp án D

Câu 3:

lim((3-4n)/5n) có giá trị bằng:

A. 3/5

B. -3/5

C. 4/5

D. -4/5

Xem đáp án

- Cách 1: Chia tử và mẫu của phân tử cho n (n là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), ta được :

Đáp án là D

- Cách 2: Sử dụng nhận xét:

khi tính lim un ta thường chia tử và mẫu của phân thức cho $n^{k}$ ( $n^{k}$ là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), từ đó được kết quả:

Nếu m < p thì lim un =0.

Nếu m =p thì lim un=am/bp

Nếu m > p thì lim un= +∞ nếu am.bp > 0; lim un= -∞ nếu am.bp < 0

Vì tử và mẫu của phân thức đã cho đều có bậc 1 nên kết quả

do đó chọn đáp án là D

Câu 4:

$l i m \frac{3 n^{2} - 2 n + 1}{4 n^{4} + 2 n + 1}$ bằng

A. 0

B. +∞

C. 3/4

D. 2/7

Xem đáp án

- Cách 1: Sử dụng nhận xét trên, vì bậc của tử thức nhỏ hơn bậc của mẫu thức nên kết quả :

Đáp án là A

- Cách 2: Chia tử và mẫu của phân thức cho n4(n4 là luỹ thừa bậc cao nhất

của n trong tử và mẫu của phân thức ta được

Đáp án A

Câu 5:

A. 0

B. +∞

C. 3/4

D. 2/7

Xem đáp án

- Cách 1: Sử dụng nhận xét trên, vì bậc của tử thức lớn hơn bậc của mẫu thức, hệ số luỹ thừa bậc cao nhất của n cả tử và mẫu là số dương nên kết quả :

Đáp án là B

- Cách 2: Chia tử và mẫu của phân thức cho n4(n4 là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức) ta được:

Đáp án B

Câu 6:

Dãy số nào sau đây có giới hạn bằng 1/5?

A. $\frac{n^{2} - 2 n}{5 n + 5 n^{2}}$

B. $\frac{1 - 2 n}{5 n + 5}$

C. $\frac{1 - 2 n^{2}}{5 n + 5}$

D. $\frac{1 - 2 n}{5 n + 5 n^{2}}$

Xem đáp án

Câu 7:

$l i m \frac{2^{n} + 3^{n}}{3^{n}}$ có giá trị bằng

A. 0

B. 1

C. 2/3

D. 5/3

Xem đáp án

Câu 8:

$l i m \frac{\sqrt{n + 4}}{\sqrt{n} + 1}$ có giá trị bằng

A. 1

B. 2

C. 4

D. +∞

Xem đáp án

Chia cả tử thức và mẫu thức cho $\sqrt{n}$

Đáp án A

Câu 9:

$l i m \frac{1 + 2 + 3 + . . . + n}{2 n^{2}}$ bằng

A. 0

B. 1/4

C. 1/2

D. +∞

Xem đáp án

Đáp án là B

Câu 10:

$l i m \frac{n + \sin 2 n}{n + 5}$ bằng:

A. 2/5

B. 1/5

C. 0

D. 1

Xem đáp án

Chia cả tử thức mẫu thức cho n , ta có:

Đáp án D

Câu 11:

$l i m (- 3 n^{3} + 2 n^{2} - 5)$ bằng:

A. -3

B. 0

C. -∞

D. +∞

Xem đáp án

Ta có:

Đáp án C

Câu 12:

$L i m (2 n^{4} + 5 n^{2} - 7 n)$ bằng

A. -∞

B. 0

C. 2

D. +∞

Xem đáp án

Ta có:

Đáp án D

Câu 13:

Dãy số nào sau đây có giới hạn là +∞?

A. $u_{n} = 9 n^{2} - 2 n^{5}$

B. $u_{n} = n^{4} - 4 n^{5}$

C. $u_{n} = 4 n^{2} - 3 n$

D. $u_{n} = n^{3} - 5 n^{4}$

Xem đáp án

Chỉ có dãy un=4n2-3n có giới hạn là +∞, các dãy còn lại đều có giới hạn là -∞.

Thật vậy, ta có: $\lim ( 4 n^{2} - 3 n) = \lim n^{2} (4 - \frac{3}{n}) = + \infty$

Vì $\lim n^{2} = + \infty; \lim (4 - \frac{3}{n}) = 4 > 0$

Đáp án C

Câu 14:

Nếu $l i m u_{n} = L, u_{n} + 9 > 0 \forall n t h ì l i m \sqrt{(u_{n} + 9)}$ bằng số nào sau đây?

A. L+9

B. L+3

C. $\sqrt{(L + 9)}$

D. $\sqrt{L + 3}$

Xem đáp án

Vì limun=L nên lim⁡(un+9)=L+9

Do đó:

Đáp án là C

Câu 15:

$l i m \frac{\sqrt{4 n^{2} + 5} - \sqrt{n + 4}}{2 n - 1}$ bằng:

A. 0

B. 1

C. 2

D. +∞

Xem đáp án

- Cách 1:

Đáp án là B

- Cách 2: Thực chất có thể coi bậc cao nhất của tử thức và mẫu thức là 1, do đó chỉ cần để ý hệ số bậc 1 của tử thức là √4, của mẫu thức là 2, từ đó tính được kết quả bằng 1. Đáp án B

Câu 16:

$\lim n (\sqrt{n^{2} + 1} - \sqrt{n^{2} - 3})$ bằng:

A. +∞

B. 4

C. 2

D. -1

Xem đáp án

Câu 17:

$l i m \frac{\sqrt{2 n + 3}}{\sqrt{2 n} + 5}$ bằng:

A. 5/7

B. 5/2

C. 1

D.+∞

Xem đáp án

Câu 18:

Tổng của cấp số nhân vô hạn : $\frac{1}{2}, - \frac{1}{4}, . . . ., \frac{{(- 1)}^{n + 1}}{2^{n}}, . . . . l à$

A. 1

B. 1/3

C. -1/3

D. (-2)/3

Xem đáp án

Câu 19:

Cho số thập phân vô hạn tuần hoàn (chu kỳ ) $a = 2, 1515151515...$ , a được biểu diễn dưới dạng phân số tối giản $a = \frac{m}{n}$ , trong đó m, n là các số nguyên dương. Tìm tổng m + n.

A. 104

B. 312

C. 38

D . 114

Xem đáp án

Câu 20:

Dãy nào sau đây có giưới hạn bằng 0?

A. ${(0, 99)}^{n}$

B. ${(- 1, 01)}^{n}$

C. ${(1, 01)}^{n}$

D. ${(- 2, 001)}^{n}$

Xem đáp án

Chọn A

Vì $0, 99 < 1$ , do đó $\lim {(0, 99)}^{n} = 0$

Câu 21:

Dãy nào sau đây không có giới hạn?

A. ${(0, 99)}^{n}$

B. ${(- 1)}^{n}$

C. ${(- 0, 98)}^{n}$

D. ${(- 0, 89)}^{n}$

Xem đáp án

Chọn B

Do đó, dãy số này không có giới hạn.

Câu 22:

Dãy nào sau đây có giới hạn bằng 0?

A. ${(5 / 4)}^{n}$

B. ${(1 / 3)}^{n}$

C. $({(- π) / 3)}^{n}$

D. $({(- 4) / 3)}^{n}$

Xem đáp án

Chọn B

Câu 23:

$l i m \frac{{(- 1)}^{n}}{n + 5}$ bằng:

A. (-1)/5

B. (-1)/6

C. -1

D. 0

Xem đáp án

Chọn D

Vì $0 < |\frac{{(- 1)}^{n}}{n + 5}| \leq \frac{1}{n + 5}$ mà $\lim \frac{1}{n + 5} = 0$

Do đó $\lim \frac{{(- 1)}^{n}}{n + 5} = 0$

Câu 24:

$l i m \frac{3 n^{4} - 2 n + 3}{4 n^{4} + 2 n + 1}$ bằng:

A. 0

B. +∞

C. 3/4

D. 4/7

Xem đáp án

Chọn C

Câu 25:

Dãy số nào sau đây có giới hạn bằng 0?

A. $u_{n} = \frac{n^{2} - 2 n}{5 n + 5 n^{2}}$

B. $u_{n} = \frac{1 - 2 n}{5 n + 5}$

C. $u_{n} = \frac{1 - 2 n^{2}}{5 n + 5}$

D. $u_{n} = \frac{1 - 2 n}{5 n + 5 n^{2}}$

Xem đáp án

Chọn D

Cách 1: Để giới hạn bằng 0 thì bậc của tử nhỏ hơn bậc của mẫu nên chỉ có phương án D thỏa mãn

Cách 2: Xét phương án D:

Câu 26:

Trong các giới hạn sau đây giới hạn nào bằng -1?

A. $l i m \frac{2 n^{2} + 3}{- 2 n^{3} + 4}$

B. $l i m \frac{2 n - 3 n^{2}}{- 2 n^{2} - 1}$

C. $l i m \frac{2 n^{2} - 3}{- 2 n^{3} + 2 n^{2}}$

D. $l i m \frac{2 n^{2} - 3}{- 2 n^{2} - 1}$

Xem đáp án

Chọn D

Để giới hạn là 1 số thực thì bậc của tử và mẫu phải bằng nhau nên loại phương án A và C.

Xét phương án D.

Câu 27:

Trong các giới hạn sau đây giới hạn nào là +∞?

A. $l i m \frac{2 n^{2} + 3}{- 2 n^{3} + 4}$

B. $l i m \frac{2 n - 3 n^{3}}{2 n^{2} - 1}$

C. $l i m \frac{2 n^{2} - 3 n^{4}}{- 2 n^{3} + 2 n^{2}}$

D. $l i m \frac{3 - 2 n^{3}}{2 n^{2} - 1}$

Xem đáp án

Chọn C

Xét phương án C:

Câu 28:

$l i m \frac{10^{4} n}{10^{4} + 2 n}$ bằng:

A. +∞

B. 10000

C. 5000

D. 1

Xem đáp án

Chọn C

Câu 29:

$l i m \frac{\sqrt[3]{n^{3} + n}}{6 n + 2}$ bằng:

A. $\frac{1}{6}$

B. $\frac{1}{4}$

C. $\frac{\sqrt[3]{2}}{6}$

D. 0

Xem đáp án

Chọn A

( Chia cả tử và mẫu cho n )

Câu 30:

$l i m \sqrt{4 - \frac{\cos 2 n}{n}}$ bằng:

A. 4

B. 2

C. $\sqrt{2}$

D. 0

Xem đáp án

Chọn B

Câu 31:

$l i m (5 n - 4 n^{3})$ bằng:

A. -∞

B. -4

C. 5

D. +∞

Xem đáp án

Chọn A

Câu 32:

Dãy số nào sau đây có giới hạn là +∞?

A. $u_{n} = 6 n^{2} - 5 n^{3}$

B. $u_{n} = n^{2} - 4 n^{3}$

C. $u_{n} = 7 n^{2} - n$

D. $u_{n} = 3 n^{3} - n^{4}$

Xem đáp án

Chọn C

Xét phương án C:

Câu 33:

Dãy nào sau đây có giới hạn là -∞?

A. $u_{n} = n^{4} - 3 n^{2}$

B. $u_{n} = 5 n^{3} - 2 n^{4}$

C. $u_{n} = 3 n^{2} - n$

D. $u_{n} = - n^{2} + 4 n^{3}$

Xem đáp án

Chọn B

Trắc nghiệm Giới hạn của dãy số có đáp án

Trắc nghiệm Giới hạn của dãy số có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương