Trắc nghiệm Toán 10 Bài tập cuối chương 4 có đáp án
Trắc nghiệm Toán 10 Bài tập cuối chương 4 có đáp án
-
215 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
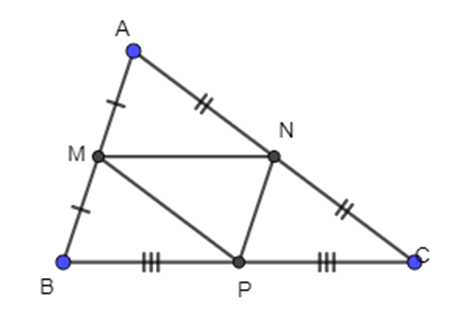
Phát biểu nào dưới đây là sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
+) Xét tam giác ABC, có:
M là trung điểm AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC và MN = 12BC
Mà BP = PC = 12BC (P là trung điểm của BC)
⇒ MN = CP = PB (1)
Vì MN // BC nên MN // CP. Khi đó →MN và →PC cùng phương. Suy ra →MN và →PC cùng hướng (2)
Từ (1) và (2) suy ra →MN = →CP. Do đó đáp án A đúng.
Tương tự MN //BC hay MN // PB. Khi đó →MN và →PB cùng phương nhưng ngược hướng (3)
Từ (1) và (3) suy ra →MN không bằng →PB. Do đó đáp án D sai.
+) Ta có →AA và →PP là các vectơ – không.
Mà mọi vectơ – không có cùng độ dài và cùng hướng nên bằng nhau
Suy ra →AA cùng hướng với →PP. Do đó đáp án B đúng.
+) Hai vec tơ →AM và →MB cùng hướng
Vì M là trung điểm của AB nên AM = MB
Suy ra →AM=→MB. Do đó đáp án C đúng.
Câu 2:
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng →CD.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Vì ABCD là hình bình hành nên AB // CD nên →BA và →CD cùng phương. Do đó →BA và →CD cùng hướng.
Mặt khác AB = CD (tính chất hình bình hành)
Suy ra →BA=→CD.
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có →MN(−1;−4). Gọi tọa độ điểm cần tìm là F(x; y).
Khi đó →MF(x−3;y+1)
Để M, N, F thẳng hàng khi →MF cùng phương với →MN hay x−3−1=y+1−4
⇔ y + 1 = 4(x – 3)
⇔ y= 4x – 12 (1)
+) Xét tọa độ P có x = 0 và y = 13 thay vào (1) ta được 13 = 4.0 – 12 là mệnh đề sai. Do đó loại P.
+) Xét tọa độ Q có x = 1 và y = -9 thay vào (1) ta được -8 = 4.1 – 12 là mệnh đề đúng. Do đó Q thỏa mãn.
+) Xét tọa độ H có x = 2 và y = 1 thay vào (1) ta được 1 = 4.2 – 12 là mệnh đề sai. Do đó loại H.
+) Xét tọa độ K có x = 3 và y = 1 thay vào (1) ta được 1 = 4.3 – 12 là mệnh đề sai. Do đó loại H.
Vậy M, N, Q thẳng hàng.
Câu 4:
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
 Xem đáp án
Xem đáp án
Đáp án đúng là C

Xét tam giác ABC vuông tại A, có:
BC2 = AB2 + AC2 (định lí Py – ta – go)
⇔ BC2 = 22 + 72 = 4 + 49 = 53
⇔ BC = √53 cm
Ta lại có M là trung điểm BC
⇒ AM = 12 BC (tính chất đường trung tuyến)
⇒ AM = √532 cm.
⇒ |→AB|=AB=√532cm
Vậy độ dài vectơ →AB là √532cm.
Câu 5:
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ →AB.
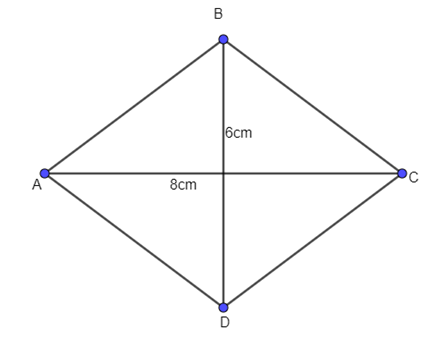
 Xem đáp án
Xem đáp án
Đáp án đúng là D
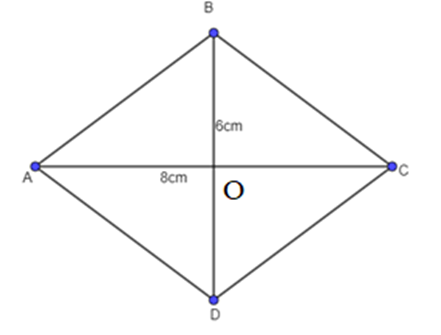
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC, cũng là trung điểm của BD.
⇒ AO = OC = AC2=82=4cm.
⇒ BO = OD = BD2=62=3cm.
Xét tam giác AOB vuông tại O, có:
AB2 = AO2 + BO2 (định lí Py – ta – go)
⇔ AB2 = 42 + 32 = 16 + 9 = 25
⇔ AB = 5 (cm)
⇒|→AB|=AB=5cm.
Vậy độ dài →AB là 5cm.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Vectơ có điểm đầu là P và điểm cuối là Q được kí hiệu là →PQ.
Câu 7:
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
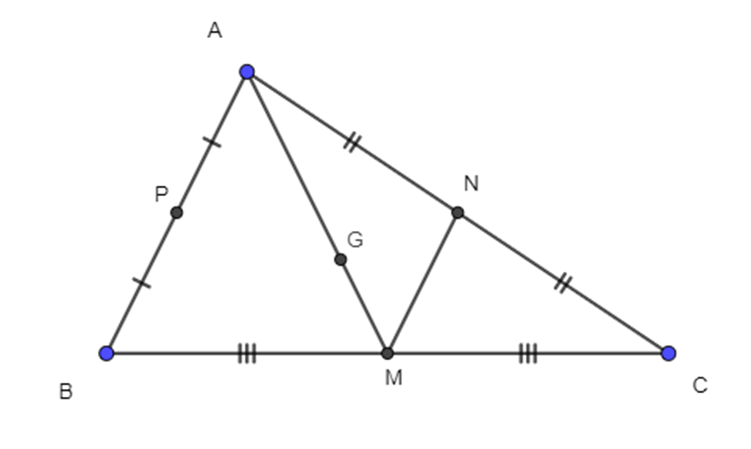
Ta có →MN = (-1; 4)
Gọi tọa độ của điểm A là A(xA; yA). Khi đó →PA(xA−2;yA+3).
Ta có →MN=→PA(tính chất đường trung bình)
Suy ra {xA−2=−1yA+3=4⇔{xA=1yA=1
⇒ A(1; 1).
Gọi tọa độ điểm B, C lần lượt là B(xB; yB) và C(xC; yC).
Vì P là trung điểm của AB nên ta có: {xB=2.2−1yB=2.(−3)−1⇔{xB=3yB=−7
⇒ B(3; -7).
Vì N là trung điểm của AC nên ta có: {xC=2.(−1)−1yC=2.5−1⇔{xC=−3yC=9
⇒ C(-3; 9).
Khi đó tọa độ trọng tâm G là {xG=1+3+(−3)3yG=1+(−7)+93⇔{xG=13yG=1
⇒G(13;1).
Câu 8:
Khi nào tích vô hướng của hai vecto →u,→v là một số dương.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Tích vô hướng của hai vecto →u,→v≠→0 được tính bởi công thức sau:
→u.→v=|→u|.|→v|.cos(→u,→v).
Vì |→u|>0,|→v|>0 nên dấu của →u.→v phụ thuộc vào dấu của cos(→u,→v).
Nếu tích vô hướng của hai vecto →u,→v là một số dương thì cos(→u,→v)>0. Do đó góc giữa hai vecto →u,→v là góc nhọn hoặc bằng 00.
Câu 9:
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto →v=(2;5). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gọi A’(x’; y’) là vị trí tàu thủy đến sau khi khởi hành 2 giờ.
Khi đó, ta có:
{x′=−3+2.2y′=2+2.5⇔{x′=1y′=12⇒A′(1;12)
Vậy sau khi khởi hành 2 giờ thì tàu thủy đến được vị trí A’(1; 12).
Câu 10:
Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
+) Trọng tâm tam giác ABD là: (11+4+73;−2+10+63)=(223;143);
+) Trọng tâm tam giác ABC là: (11+4+(−2)3;−2+10+23)=(133;103);
+) Trọng tâm tam giác ACD là: (11+(−2)+73;−2+2+63)=(163;2);
+) Trọng tâm tam giác BCD là: (4+(−2)+73;10+2+63) = (3; 6).
Vậy G là trọng tâm tam giác BCD.
Câu 11:
Cho hình vẽ sau:
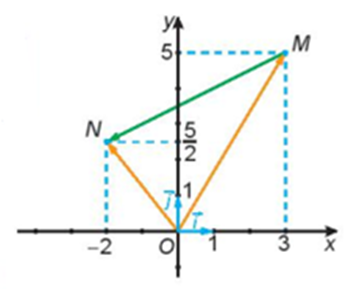
Hãy biểu thị mỗi vecto →OM,→ON theo các vecto →i,→j.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
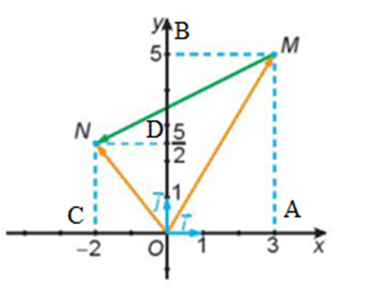
Xét hình bình hành OAMB, có:
→OM=→OA+→OB=3→i+5→j (quy tắc hình bình hành)
Xét hình bình hành OCND, có:
→ON=→OC+→OD=−2→i+52→j (quy tắc hình bình hành) .
Câu 12:
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
→x(-1; 3); →y(2;−13) ; →z(−25;15); →w(4; -2).
 Xem đáp án
Xem đáp án
Đáp án đúng là A
+) Xét cặp vectơ →z và →w ta có: −254=15−2. Do đó cặp vectơ →z và →w cùng phương.
Các cặp vectơ còn lại không cùng phương, thật vậy
+) Xét cặp vectơ →y và →z ta có: 2−25≠−1315. Do đó cặp vectơ →y và →z không cùng phương.
Vì cặp vectơ →z và →w cùng phương nên cặp vectơ →y và →w không cùng phương.
+) Xét cặp vectơ →y và →x ta có: 2−1≠−133. Do đó cặp vectơ →y và →x không cùng phương.
+) Xét cặp vectơ →x và →z ta có: −1−25≠315. Do đó cặp vectơ →x và →z không cùng phương.
Vì cặp vectơ →z và →w cùng phương nên cặp vectơ →x và →w không cùng phương.
Vậy chỉ có duy nhất một cặp vectơ cùng phương
Câu 13:
Cho tam giác ABC có bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Các vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C là: →AB,→AC,→BC,→BA,→CA,→CB.
Vậy tổng có 6 vectơ.
Câu 14:
Điền từ thích hợp vào dấu (…) để được mệnh đề đúng. “Hai vectơ ngược hướng thì …”:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Hai vectơ ngược hướng thì cùng phương.
Câu 15:
Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Vectơ - không cùng hướng với mọi vectơ nên cùng phương với mọi vectơ.
Mà có vô số vec tơ – không. Do đó B đúng.
Câu 16:
Cho hình vẽ:
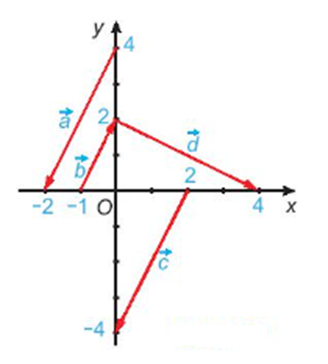
Có bao nhiêu cặp vectơ không cùng phương trên hình vẽ?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Quan sát hình vẽ ta thấy:
Các cặp vectơ không cùng phương là: →a và →d, →b và →d, →c và →d.
Vậy có tất cả 3 cặp vectơ không cùng phương.
Câu 17:
Trong mặt phẳng tọa độ Oxy, cho →u=−5→i+6→j. Khi đó tọa độ của vectơ →ulà:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có →u=−5→i+6→j. Khi đó toạ độ của →u là →u(-5; 6).
Câu 18:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài →BC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có →BC = (3 – 1; -1 – 2) = (2; -3).
⇒|→BC|=√22+(−3)2=√13.
Câu 19:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có hai vecto →OA(2;1),→OB(3;3) không cùng phương (vì 23≠13). Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Suy ra các điểm O, A, B không thẳng hàng
Để OABM là hình bình hành khi và chỉ khi →OA=→MB
Ta có: →OA(2;1),→MB(3−x;3−y) nên
{2=3−x1=3−y⇔{x=1y=2⇒M(1;2).
Vậy điểm cần tìm là M(1;2).
Câu 20:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có M(1;3) ⇒→OM(1;3)⇒OM=√12+32=√10.
Ta lại có N(4;2) ⇒→ON(4;2)⇒ON=√42+22=√20=2√5.
⇒→MN=→ON−→OM=(−3;1)⇒MN=√(−3)2+12=√10
Xét tam giác OMN, có: OM=MN=√10 nên tam giác OMN cân tại M.
Ta có: ON2=(2√5)2=20,OM2+MN2=(√10)2+(√10)2=20
⇒ON2=OM2+MN2
Theo định lí Py – ta – go đảo suy ra tam giác OMN vuông tại O.
Do đó tam giác OMN vuông cân tại M.
Câu 21:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì G là trọng tâm tam giác ABC nên ta có:
\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + x{ & _C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + y{ & _C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{ccccc}x{ & _C} = 3.{x_G} - \left( {{x_A} + {x_B}} \right) = 3.( - 3) - (1 + 2) = - 12\\y{ & _C} = 3{y_G} - ({y_A} + {y_B}) = 3.2 - \left( {3 + 4} \right) = - 1\end{array} \right.
⇒ G(-12; -1).
Câu 22:
Trong mặt phẳng tọa độ Oxy, cho các vecto →b(4;−1) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để →MN=→b.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →MN=(0−(−3x);−2+y−(−1))=(3x;−1+y)
Để →MN=→b⇔{3x=4−1+y=−1⇔{x=43y=0.
Vậy x = 43, y = 0.
Câu 23:
Trong mặt phẳng tọa độ Oxy, cho các điểm A(k−13;5), B(-2; 12) và
C(23;k−2). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →AC=(23−(k−13);k−2−5)=(1−k;k−7),
→BC=(23−(−2);k−2−12)=(83;k−14)
Để ba điểm A, B, C thẳng hàng khi →AC và →BC cùng phương
⇔1−k83=k−7k−14
⇔ (1 – k)(k – 14) = 83(k – 7)
⇔ - k2 + 15k – 14 = 83k – 563
⇔ - 3k2 + 45k – 42 = 8k – 56
⇔ 3k2 – 37k – 14 = 0
⇔ k1 ≈ 12,7 hoặc k2 ≈ -0,37.
Ta thấy k1 là giá trị dương nằm trong khoảng (12; 14).
Câu 24:
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →a.→b=1.(−1)+(−1).1=−1+(−1)=−2≠0. Suy ra hai vecto →a,→b không vuông góc với nhau. Do đó A sai.
Ta có: →n.→k=1.2+1.0=2+0=2≠0. Suy ra hai vecto →n,→k không vuông góc. Do đó B sai.
Ta có: →u.→v=2.4+3.6=8+18=26≠0. Suy ra hai vecto →u,→v không vuông góc. Do đó C sai.
Ta có: →z.→t=a.(−b)+b.a=−ab+ab=0. Suy ra hai vecto →z,→t vuông góc với nhau. Do đó D đúng.
Câu 25:
Góc giữa vectơ →a(−1;−1) và vecto →b(−1;0) có số đo bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →a.→b=(−1).(−1)+(−1).0=1,|→a|=√(−1)2+(−1)2=√2,|→b|=√(−1)2+02=1.
⇒cos(→a.→b)=→a.→b|→a|.|→b|=1√2⇒(→a.→b)=45∘.
Vậy góc giữa hai vec tơ →a và →blà 45°.
Câu 26:
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Vì ABCD là hình vuông cạnh a nên AB = BC = a, BD = AC = a√2.
Ta có →AB(a;0), →BD(−a;a), →AC(a;a), →BC(0;a), →BA(−a;0).
Khi đó:
+) →AB.→BD=a.(−a)+0.a=−a2
⇒cos(→AB,→BD)=→AB.→BD|→AB|.|→BD|=−a2a.a√2=−1√2⇒(→AB,→BD)=1350. Do đó A sai.
+) →AC.→BC = a.0 + a.a = a2
⇒cos(→AC,→BC)=→AC.→BC|→AC|.|→BC|=a2a.a√2=1√2⇒(→AC,→BC)=450. Do đó B đúng
+) →AC.→BD=a.(−a)+a.a=0. Do đó C sai.
+) →BA.→BD = -a.(-a) + 0.a = a2. Do đó D sai.
Câu 27:
Khi nào thì hai vectơ →a và →b vuông góc?
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Hai vec tơ →a và →b vuông góc khi →a.→b= 0.
Câu 28:
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn →AB.→AC=2
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có: →AB(1;1),→AC(2x;3x2−3).
Khi đó: →AB.→AC = 1.2x + 1.(3x2 – 3) = 3x2 + 2x – 3
Mà →AB.→AC = 2 nên 3x2 + 2x – 3 = 2
⇔ 3x2 + 2x – 5 = 0
⇔[x=1x=−53
Tổng hai nghiệm là 1 + (−53) = 33+(−53)=−23.
Vậy tổng hai nghiệm là −23.
Câu 29:
Trong mặt phẳng tọa độ Oxy, cho các vecto →u(2;3x−3) và →v(−1;−2). Có bao nhiêu giá trị nguyên của x thỏa mãn |→u|=|2→v|.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Độ dài của vectơ →u là |→u|=√22+(3x−3)2=√4+(3x−3)2.
Độ dài của vectơ →v là |→v|=√(−1)2+(−2)2=√5.
Suy ra độ dài của vectơ 2→v là 2|→v|=2.√(−1)2+(−2)2=2√5.
Để |→u| = 2|→v| thì√4+(3x−3)2=2√5
⇔ 4 + (3x – 3)2 = 20
⇔ (3x – 3)2 = 16
⇔ [3x+3=43x+3=−4
⇔ [3x=13x=−7
⇔ [x=13x=−73
Ta thấy các giá trị 13 hay −73 đều không là các giá trị nguyên. Do đó không tồn tại giá trị nguyên nào của x thỏa mãn điều kiện đầu bài.
Câu 30:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có →MN(−1;−4). Gọi tọa độ điểm cần tìm là F(x; y).
Khi đó →MF(x−3;y+1)
Để M, N, F thẳng hàng khi →MF cùng phương với →MN hay x−3−1=y+1−4
⇔ y + 1 = 4(x – 3)
⇔ y= 4x – 12 (1)
+) Xét tọa độ P có x = 0 và y = 13 thay vào (1) ta được 13 = 4.0 – 12 là mệnh đề sai. Do đó loại P.
+) Xét tọa độ Q có x = 1 và y = -9 thay vào (1) ta được -8 = 4.1 – 12 là mệnh đề đúng. Do đó Q thỏa mãn.
+) Xét tọa độ H có x = 2 và y = 1 thay vào (1) ta được 1 = 4.2 – 12 là mệnh đề sai. Do đó loại H.
+) Xét tọa độ K có x = 3 và y = 1 thay vào (1) ta được 1 = 4.3 – 12 là mệnh đề sai. Do đó loại H.
Vậy M, N, Q thẳng hàng.
