Trắc nghiệm Toán 10 Bài 10. Vecto trong mặt phẳng tọa độ có đáp án
Trắc nghiệm Toán 10 Bài 10. Vecto trong mặt phẳng tọa độ có đáp án
-
2036 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho →u=−5→i+6→j. Khi đó tọa độ của vectơ →ulà:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có →u=−5→i+6→j. Khi đó toạ độ của →u là →u(-5; 6).
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài →BC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có →BC = (3 – 1; -1 – 2) = (2; -3).
⇒|→BC|=√22+(−3)2=√13.
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có hai vecto →OA(2;1),→OB(3;3) không cùng phương (vì 23≠13). Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Suy ra các điểm O, A, B không thẳng hàng
Để OABM là hình bình hành khi và chỉ khi →OA=→MB
Ta có: →OA(2;1),→MB(3−x;3−y) nên
{2=3−x1=3−y⇔{x=1y=2⇒M(1;2).
Vậy điểm cần tìm là M(1;2).
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có M(1;3) ⇒→OM(1;3)⇒OM=√12+32=√10.
Ta lại có N(4;2) ⇒→ON(4;2)⇒ON=√42+22=√20=2√5.
⇒→MN=→ON−→OM=(−3;1)⇒MN=√(−3)2+12=√10
Xét tam giác OMN, có: OM=MN=√10 nên tam giác OMN cân tại M.
Ta có: ON2=(2√5)2=20,OM2+MN2=(√10)2+(√10)2=20
⇒ON2=OM2+MN2
Theo định lí Py – ta – go đảo suy ra tam giác OMN vuông tại O.
Do đó tam giác OMN vuông cân tại M.
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì G là trọng tâm tam giác ABC nên ta có:
\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + x{ & _C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + y{ & _C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{ccccc}x{ & _C} = 3.{x_G} - \left( {{x_A} + {x_B}} \right) = 3.( - 3) - (1 + 2) = - 12\\y{ & _C} = 3{y_G} - ({y_A} + {y_B}) = 3.2 - \left( {3 + 4} \right) = - 1\end{array} \right.
⇒ G(-12; -1).
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho các vecto →b(4;−1) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để →MN=→b.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →MN=(0−(−3x);−2+y−(−1))=(3x;−1+y)
Để →MN=→b⇔{3x=4−1+y=−1⇔{x=43y=0.
Vậy x = 43, y = 0.
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho các điểm A(k−13;5), B(-2; 12) và
C(23;k−2). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →AC=(23−(k−13);k−2−5)=(1−k;k−7),
→BC=(23−(−2);k−2−12)=(83;k−14)
Để ba điểm A, B, C thẳng hàng khi →AC và →BC cùng phương
⇔1−k83=k−7k−14
⇔ (1 – k)(k – 14) = 83(k – 7)
⇔ - k2 + 15k – 14 = 83k – 563
⇔ - 3k2 + 45k – 42 = 8k – 56
⇔ 3k2 – 37k – 14 = 0
⇔ k1 ≈ 12,7 hoặc k2 ≈ -0,37.
Ta thấy k1 là giá trị dương nằm trong khoảng (12; 14).
Câu 8:
Trong mặt phẳng tọa độ Oxy, cho các vecto →u(2;3x−3) và →v(−1;−2). Có bao nhiêu giá trị nguyên của x thỏa mãn |→u|=|2→v|.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Độ dài của vectơ →u là |→u|=√22+(3x−3)2=√4+(3x−3)2.
Độ dài của vectơ →v là |→v|=√(−1)2+(−2)2=√5.
Suy ra độ dài của vectơ 2→v là 2|→v|=2.√(−1)2+(−2)2=2√5.
Để |→u| = 2|→v| thì√4+(3x−3)2=2√5
⇔ 4 + (3x – 3)2 = 20
⇔ (3x – 3)2 = 16
⇔ [3x+3=43x+3=−4
⇔ [3x=13x=−7
⇔ [x=13x=−73
Ta thấy các giá trị 13 hay −73 đều không là các giá trị nguyên. Do đó không tồn tại giá trị nguyên nào của x thỏa mãn điều kiện đầu bài.
Câu 9:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có →MN(−1;−4). Gọi tọa độ điểm cần tìm là F(x; y).
Khi đó →MF(x−3;y+1)
Để M, N, F thẳng hàng khi →MF cùng phương với →MN hay x−3−1=y+1−4
⇔ y + 1 = 4(x – 3)
⇔ y= 4x – 12 (1)
+) Xét tọa độ P có x = 0 và y = 13 thay vào (1) ta được 13 = 4.0 – 12 là mệnh đề sai. Do đó loại P.
+) Xét tọa độ Q có x = 1 và y = -9 thay vào (1) ta được -8 = 4.1 – 12 là mệnh đề đúng. Do đó Q thỏa mãn.
+) Xét tọa độ H có x = 2 và y = 1 thay vào (1) ta được 1 = 4.2 – 12 là mệnh đề sai. Do đó loại H.
+) Xét tọa độ K có x = 3 và y = 1 thay vào (1) ta được 1 = 4.3 – 12 là mệnh đề sai. Do đó loại H.
Vậy M, N, Q thẳng hàng.
Câu 10:
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
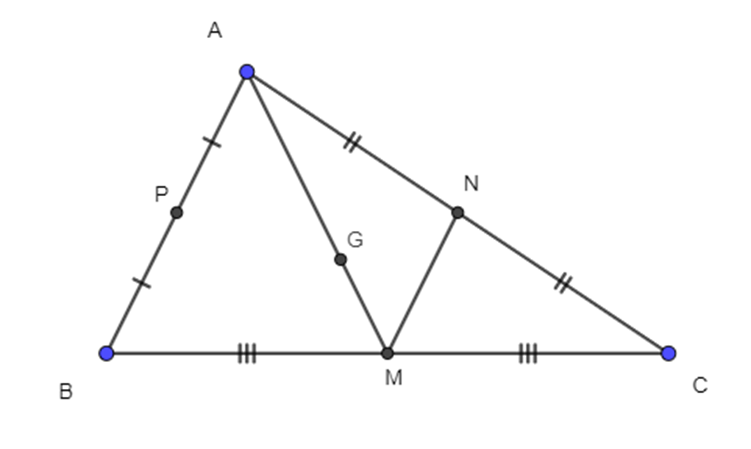
Ta có →MN = (-1; 4)
Gọi tọa độ của điểm A là A(xA; yA). Khi đó →PA(xA−2;yA+3).
Ta có →MN=→PA(tính chất đường trung bình)
Suy ra {xA−2=−1yA+3=4⇔{xA=1yA=1
⇒ A(1; 1).
Gọi tọa độ điểm B, C lần lượt là B(xB; yB) và C(xC; yC).
Vì P là trung điểm của AB nên ta có: {xB=2.2−1yB=2.(−3)−1⇔{xB=3yB=−7
⇒ B(3; -7).
Vì N là trung điểm của AC nên ta có: {xC=2.(−1)−1yC=2.5−1⇔{xC=−3yC=9
⇒ C(-3; 9).
Khi đó tọa độ trọng tâm G là {xG=1+3+(−3)3yG=1+(−7)+93⇔{xG=13yG=1
⇒G(13;1).
Câu 11:
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
→x(-1; 3); →y(2;−13) ; →z(−25;15); →w(4; -2).
 Xem đáp án
Xem đáp án
Đáp án đúng là A
+) Xét cặp vectơ →z và →w ta có: −254=15−2. Do đó cặp vectơ →z và →w cùng phương.
Các cặp vectơ còn lại không cùng phương, thật vậy
+) Xét cặp vectơ →y và →z ta có: 2−25≠−1315. Do đó cặp vectơ →y và →z không cùng phương.
Vì cặp vectơ →z và →w cùng phương nên cặp vectơ →y và →w không cùng phương.
+) Xét cặp vectơ →y và →x ta có: 2−1≠−133. Do đó cặp vectơ →y và →x không cùng phương.
+) Xét cặp vectơ →x và →z ta có: −1−25≠315. Do đó cặp vectơ →x và →z không cùng phương.
Vì cặp vectơ →z và →w cùng phương nên cặp vectơ →x và →w không cùng phương.
Vậy chỉ có duy nhất một cặp vectơ cùng phương
Câu 12:
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto →v=(2;5). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gọi A’(x’; y’) là vị trí tàu thủy đến sau khi khởi hành 2 giờ.
Khi đó, ta có:
{x′=−3+2.2y′=2+2.5⇔{x′=1y′=12⇒A′(1;12)
Vậy sau khi khởi hành 2 giờ thì tàu thủy đến được vị trí A’(1; 12).
Câu 13:
Cho hình vẽ sau:
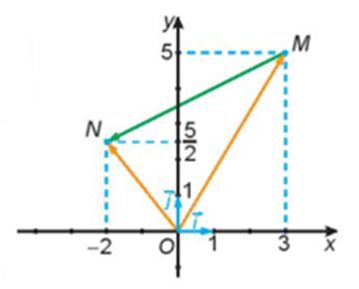
Hãy biểu thị mỗi vecto →OM,→ON theo các vecto →i,→j.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
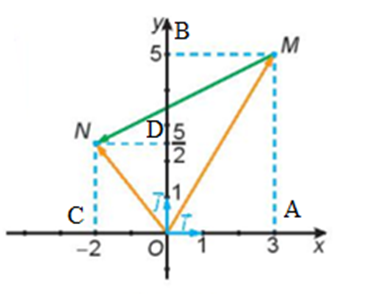
Xét hình bình hành OAMB, có:
→OM=→OA+→OB=3→i+5→j (quy tắc hình bình hành)
Xét hình bình hành OCND, có:
→ON=→OC+→OD=−2→i+52→j (quy tắc hình bình hành) .
Câu 14:
Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
+) Trọng tâm tam giác ABD là: (11+4+73;−2+10+63)=(223;143);
+) Trọng tâm tam giác ABC là: (11+4+(−2)3;−2+10+23)=(133;103);
+) Trọng tâm tam giác ACD là: (11+(−2)+73;−2+2+63)=(163;2);
+) Trọng tâm tam giác BCD là: (4+(−2)+73;10+2+63) = (3; 6).
Vậy G là trọng tâm tam giác BCD.
Câu 15:
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2). Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD. Tổng x + y bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Để O(0;0) là tọa độ trọng tâm tam giác ABD thì:
{0=1+2+x30=3+4+y3⇔{x+3=0y+7=0⇔{x=−3y=−7
Suy ra D(-3;-7) thì O(0;0) là trọng tâm tam giác ABD.
Vậy tổng x + y = -3 + (-7) = -10.
