Trắc nghiệm Toán 10 Bài 11. Tích vô hướng của hai vecto có đáp án
Trắc nghiệm Toán 10 Bài 11. Tích vô hướng của hai vecto có đáp án
-
2050 lượt thi
-
16 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →a.→b=1.(−1)+(−1).1=−1+(−1)=−2≠0. Suy ra hai vecto →a,→b không vuông góc với nhau. Do đó A sai.
Ta có: →n.→k=1.2+1.0=2+0=2≠0. Suy ra hai vecto →n,→k không vuông góc. Do đó B sai.
Ta có: →u.→v=2.4+3.6=8+18=26≠0. Suy ra hai vecto →u,→v không vuông góc. Do đó C sai.
Ta có: →z.→t=a.(−b)+b.a=−ab+ab=0. Suy ra hai vecto →z,→t vuông góc với nhau. Do đó D đúng.
Câu 2:
Góc giữa vectơ →a(−1;−1) và vecto →b(−1;0) có số đo bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có: →a.→b=(−1).(−1)+(−1).0=1,|→a|=√(−1)2+(−1)2=√2,|→b|=√(−1)2+02=1.
⇒cos(→a.→b)=→a.→b|→a|.|→b|=1√2⇒(→a.→b)=45∘.
Vậy góc giữa hai vec tơ →a và →blà 45°.
Câu 3:
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Vì ABCD là hình vuông cạnh a nên AB = BC = a, BD = AC = a√2.
Ta có →AB(a;0), →BD(−a;a), →AC(a;a), →BC(0;a), →BA(−a;0).
Khi đó:
+) →AB.→BD=a.(−a)+0.a=−a2
⇒cos(→AB,→BD)=→AB.→BD|→AB|.|→BD|=−a2a.a√2=−1√2⇒(→AB,→BD)=1350. Do đó A sai.
+) →AC.→BC = a.0 + a.a = a2
⇒cos(→AC,→BC)=→AC.→BC|→AC|.|→BC|=a2a.a√2=1√2⇒(→AC,→BC)=450. Do đó B đúng
+) →AC.→BD=a.(−a)+a.a=0. Do đó C sai.
+) →BA.→BD = -a.(-a) + 0.a = a2. Do đó D sai.
Câu 4:
Khi nào thì hai vectơ →a và →b vuông góc?
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Hai vec tơ →a và →b vuông góc khi →a.→b= 0.
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn →AB.→AC=2
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có: →AB(1;1),→AC(2x;3x2−3).
Khi đó: →AB.→AC = 1.2x + 1.(3x2 – 3) = 3x2 + 2x – 3
Mà →AB.→AC = 2 nên 3x2 + 2x – 3 = 2
⇔ 3x2 + 2x – 5 = 0
⇔[x=1x=−53
Tổng hai nghiệm là 1 + (−53) = 33+(−53)=−23.
Vậy tổng hai nghiệm là −23.
Câu 6:
Khi nào tích vô hướng của hai vecto →u,→v là một số dương.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Tích vô hướng của hai vecto →u,→v≠→0 được tính bởi công thức sau:
→u.→v=|→u|.|→v|.cos(→u,→v).
Vì |→u|>0,|→v|>0 nên dấu của →u.→v phụ thuộc vào dấu của cos(→u,→v).
Nếu tích vô hướng của hai vecto →u,→v là một số dương thì cos(→u,→v)>0. Do đó góc giữa hai vecto →u,→v là góc nhọn hoặc bằng 00.
Câu 7:
Khi nào thì (→u.→v)2=→u2.→v2?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có: →u.→v=|→u|.|→v|.cos(→u,→v)
⇔(→u.→v)2=[|→u|.|→v|.cos(→u,→v)]2=→u2.→v2.cos2(→u,→v)
Để (→u.→v)2=→u2.→v2 thì cos2(→u,→v)=1⇔[cos(→u,→v)=1cos(→u,→v)=−1⇔[(→u,→v)=00(→u,→v)=1800
Vậy khi góc giữa hai vecto →u,→v là 00 hoặc 1800 thì (→u.→v)2=→u2.→v2.
Câu 8:
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính →AB.→AC theo a, b, c.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
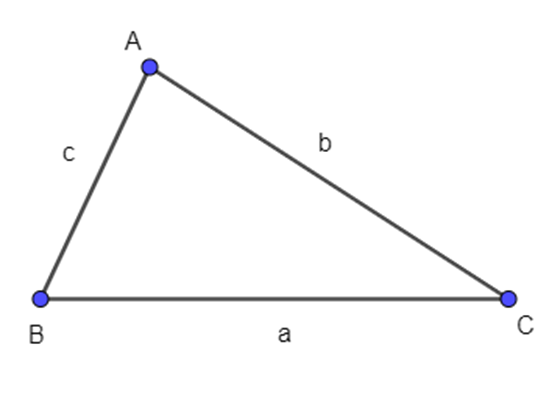
Ta có: →AB.→AC=AB.AC.cos(→AB.→AC)=AB.AC.cosBAC=bc.cosBAC
Theo định lí cos, ta có:
cosBAC=b2+c2−a22bc
→AB.→AC=bc.b2+c2−a22bc=b2+c2−a22.
Vậy →AB.→AC=b2+c2−a22.
Câu 9:
Tính tích vô hướng của hai vectơ →u(1;−3),→v(√7;−2) là k. Nhận xét nào sau đây đúng về giá trị của k.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Tích vô hướng của hai vecto k=→u.→v=1.√7+(−3).(−2)=√7+6.
Do đó k là số vô tỉ.
Câu 10:
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vecto →a và →b trong trường hợp →a(3;1),→b(2;4).
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có: →a.→b=3.2+1.4=10
|→a|=√32+12=√10,|→b|=√22+42=2√5
→a.→b=|→a|.|→b|.cos(→a,→b)⇒cos(→a,→b)=→a.→b|→a|.|→b|=10√10.2√5=1√2⇒(→a,→b)=450.
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì I là trung điểm của AB nên ta có: →IA+→IB=→0 hay →IB=−→IA.
Xét →MA.→MB=(→MI+→IA).(→MI+→IB)
=→MI2+→MI.→IB+→MI.→IA+→IB.→IA
=→MI2+→MI.(→IB+→IA)+→IB.→IA
=→MI2+(−→IA).→IA
=→MI2−→IA2
=MI2−IA2.
Câu 12:
Cho tam giác ABC với A(-1;2), B(8;-1), C(8;8). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có:
→AB=(9;−3)⇒AB=√92+(−3)2=3√10.
→AC(9;6)⇒AC=√92+62=3√13.
→BC(0;9)⇒BC=√02+92=9.
Ta lại có:
→AB.→AC=AB.AC.cos^BAC
⇔9.9+(−3).6=3√10.3√13.cos^BAC
⇔63=9√130.cos^BAC
⇔cos^BAC=7√130⇔^BAC≈52,13∘.
Áp dụng định lí Sin trong tam giác ta được:
BCsin^BAC=2R⇔9sin52,13∘=2R⇔R≈5,7.
Câu 13:
Tìm điều kiện của →u,→v để →u.→v=−|→u|.|→v|.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có: →u.→v=|→u|.|→v|.cos(→u,→v)
Để →u.→v=−|→u|.|→v| thì cos(→u,→v)=−1⇔(→u,→v)=1800
Suy ra →u,→v là hai vectơ ngược hướng.
Câu 14:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; -3), B(5; 2). Tìm điểm M thuộc tia Oy để góc ^AMB=900.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Gọi M có tọa độ M(0; m).
Vì M thuộc tia Oy nên m ≥ 0.
Ta có: →AM(−1;m+3),→BM(−5;m−2).
⇒→AM.→BM=(−1).(−5)+(m+3).(m−2)=m2+m−1.
Để ^AMB=900 thì →AM.→BM=0
⇔m2+m−1=0⇔[m=−1+√52m=−1−√52
Ta thấy m=−1+√52 (thỏa mãn) và m=−1−√52 (không thỏa mãn)
Vậy M(0;−1+√52).
Câu 15:
Cho tam giác ABC có trọng tâm G. Với điểm M bất kì, đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
MA2+MB2+MC2=→MA2+→MB2+→MC2
=(→MG+→GA)2+(→MG+→GB)2+(→MG+→GC)2
=→MG2+2→MG.→GA+→GA2+→MG2+2→MG.→GB+→GB2+→MG2+2→MG.→GC+→GC2
=3→MG2+2→MG.(→GA+→GB+→GC)+→GA2+→GB2+→GC2
Ta có: →GA+→GB+→GC=→0 (tính chất trọng tâm tam giác)
⇒→MG.(→GA+→GB+→GC)=→MG.→0=0
⇒MA2+MB2+MC2=3→MG2+→GA2+→GB2+→GC2.
Câu 16:
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(-3;1), B(2;4), C(2;-2). Gọi H(x; y) là trực tâm của tam giác ABC. Tính S = 5x + y.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gọi trực tâm H của tam giác ABC có tọa độ là H(x;y)
Khi đó, ta có: →AH(x+3;y−1);→BC(0;−6);→BH(x−2;y−4);→AC(5;−3)
Vì AH⊥BC⇒→AH.→BC=0⇔(x+3).0+(y−1).(−6)=0⇔y=1.
Vì BH⊥AC⇒→BH.→AC=0⇔(x−2).5+(y−4).(−3)=0
⇔5x−10−3y+12=0
⇔5x−3y=−2
Mà y = 1 ⇒5x−3.1=−2⇔x=15.
Suy ra S = 5.15 + 1 = 2.
