Câu hỏi:
18/12/2023 110
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
A. 0;
A. 0;
B. 1;
B. 1;
C. 2;
C. 2;
D. 3.
D. 3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là A
Độ dài của vectơ \(\overrightarrow u \) là \(\left| {\overrightarrow u } \right| = \sqrt {{2^2} + {{\left( {3x - 3} \right)}^2}} = \sqrt {4 + {{\left( {3x - 3} \right)}^2}} \).
Độ dài của vectơ \(\overrightarrow v \) là \(\left| {\overrightarrow v } \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \).
Suy ra độ dài của vectơ 2\(\overrightarrow v \) là 2\(\left| {\overrightarrow v } \right| = 2.\sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = 2\sqrt 5 \).
Để \(\left| {\overrightarrow u } \right|\) = 2\(\left| {\overrightarrow v } \right|\) thì\(\sqrt {4 + {{\left( {3x - 3} \right)}^2}} = 2\sqrt 5 \)
⇔ 4 + (3x – 3)2 = 20
⇔ (3x – 3)2 = 16
⇔ \(\left[ \begin{array}{l}3x + 3 = 4\\3x + 3 = - 4\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}3x = 1\\3x = - 7\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = \frac{1}{3}\\x = - \frac{7}{3}\end{array} \right.\)
Ta thấy các giá trị \(\frac{1}{3}\) hay \( - \frac{7}{3}\) đều không là các giá trị nguyên. Do đó không tồn tại giá trị nguyên nào của x thỏa mãn điều kiện đầu bài.
Đáp án đúng là A
Độ dài của vectơ \(\overrightarrow u \) là \(\left| {\overrightarrow u } \right| = \sqrt {{2^2} + {{\left( {3x - 3} \right)}^2}} = \sqrt {4 + {{\left( {3x - 3} \right)}^2}} \).
Độ dài của vectơ \(\overrightarrow v \) là \(\left| {\overrightarrow v } \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \).
Suy ra độ dài của vectơ 2\(\overrightarrow v \) là 2\(\left| {\overrightarrow v } \right| = 2.\sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = 2\sqrt 5 \).
Để \(\left| {\overrightarrow u } \right|\) = 2\(\left| {\overrightarrow v } \right|\) thì\(\sqrt {4 + {{\left( {3x - 3} \right)}^2}} = 2\sqrt 5 \)
⇔ 4 + (3x – 3)2 = 20
⇔ (3x – 3)2 = 16
⇔ \(\left[ \begin{array}{l}3x + 3 = 4\\3x + 3 = - 4\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}3x = 1\\3x = - 7\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = \frac{1}{3}\\x = - \frac{7}{3}\end{array} \right.\)
Ta thấy các giá trị \(\frac{1}{3}\) hay \( - \frac{7}{3}\) đều không là các giá trị nguyên. Do đó không tồn tại giá trị nguyên nào của x thỏa mãn điều kiện đầu bài.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
Câu 5:
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
Câu 7:
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
Câu 9:
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
Câu 10:
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
Câu 12:
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
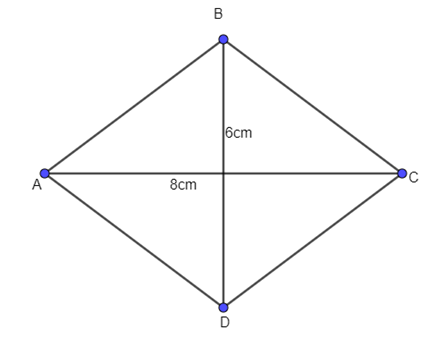
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).

Câu 13:
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
Câu 14:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Câu 15:
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
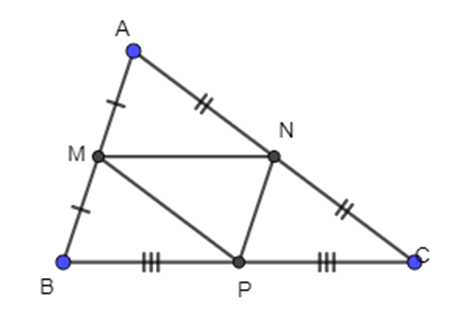
Phát biểu nào dưới đây là sai.
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.

Phát biểu nào dưới đây là sai.


