Trắc nghiệm Toán 10 Bài 9. Tích của vectơ với một số có đáp án
Trắc nghiệm Toán 10 Bài 9. Tích của vectơ với một số có đáp án
-
218 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho vectơ →a≠→0 với số thực k như thế nào thì vectơ k→a ngược hướng với vectơ →a.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Tích của một vectơ →a≠→0với số thực k < 0 là một vec tơ kí hiệu k→a ngược hướng với vectơ →a.
Câu 2:
Cho vectơ →a, →b và hai số thực k, t. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có (k + t)→a = k→a + t→a. Do đó B sai.
Câu 3:
Cho ba điểm A, B, C phân biệt sao cho →AB=k→AC.Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
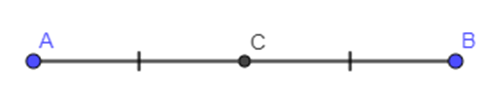
Vì C là trung điểm của đoạn thẳng AB nên AC = 2AB.
Ta có →AC,→AB là hai vectơ cùng hướng nên →AC=2→AB. Suy ra k = 2 > 1.
Vậy k thỏa mãn điều kiện k > 1.
Câu 4:
Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn →KA+2→KB=→0.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gọi I là trung điểm của đoạn thẳng AB. Khi đó →IA+→IB=→0
Xét đẳng thức: →KA+2→KB=→0
⇔→KI+→IA+2(→KI+→IB)=→0
⇔3→KI+→IA+2→IB=→0
⇔3→KI+(→IA+→IB)+→IB=→0
⇔3→KI+→0+→IB=→0
⇔→KI=−13→IB hay →IK=13→IB
Vì vậy điểm K là điểm nằm giữa I và B thỏa mãn IK=13IB.
Câu 5:
Cho tam giác ABC có đường trung tuyến AM. Khi đó →AM=a→AB+b→AC. Tính S = a + 2b.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
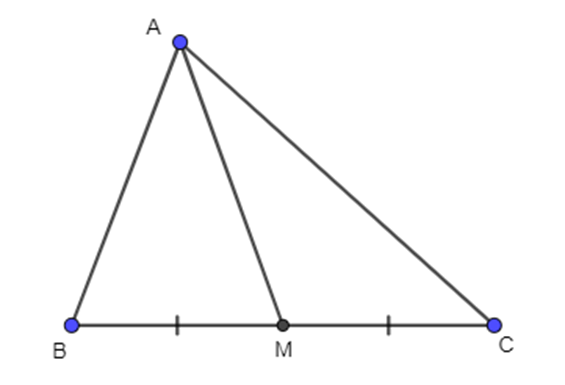
Ta có: →AB+→AC=2→AM
⇔ →AM=12→AB+12→AC
⇒ a = 12, b = 12.
⇒ S = a + 2b = 12 + 2.12 = 12 + 1 = 32.
Vậy S = 32.Câu 6:
Các tam giác ABC có trọng tâm G; M, N lần lượt là trung điểm của BC và AB. Biểu thị →MG thông qua hai vec tơ →AB,→AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có: →NG=→AG−→AN=23→AM−12→AB
=23(12→AB+12→AC)−12→AB
=13→AB−12→AB+12→AC
=−16→AB+12→AC.
Vậy →NG=−16→AB+13→AC.
Câu 7:
Cho tam giác ABC có G là trọng tâm tam giác. Hãy xác định điểm M để →MA+→MB+2→MC=→0.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Vì G là trọng tâm tam giác ABC nên →GA+→GB+→GC=→0.
Xét →MA+→MB+2→MC=→0
⇔→MG+→GA+→MG+→GB+2(→MG+→GC)=→0
⇔4→MG+(→GA+→GB+→GC)+→GC=→0
⇔4→MG+→GC=→0
⇔4→MG=−→GC
⇔→GM=14→GC.
Vậy G là điểm nằm giữa G và C sao cho GM=14GC.
Câu 8:
Trong hình vẽ, hãy biểu thị mỗi vectơ →u,→vhai vectơ →a,→b, tức là tìm các số x, y, z, t để →u=x→a+y→b,→v=t→a+z→b.
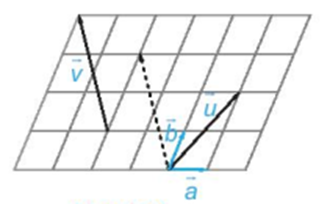
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có hình vẽ sau:
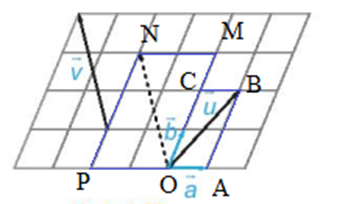
Xét hình bình hành OABC, có:
→OA=→a,→OC=2→b,→OB=→u
Khi đó, ta có:
→u=→OB=→OA+→OC=→a+2→b (quy tắc hình bình hành)
Xét hình bình hành OMNP, có:
→ON=→v,→OM=3→b,→OP=−2→a
Khi đó, ta có:
→v=→ON=→OM+→OP=3→b−2→a=−2→a+3→b.
Vậy →u=→a+2→b,→v=−2→a+3→b.
Câu 9:
Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC sao cho AF = 13AC. Hãy xác định điểm M để →MA+3→MB+2→MC=→0.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
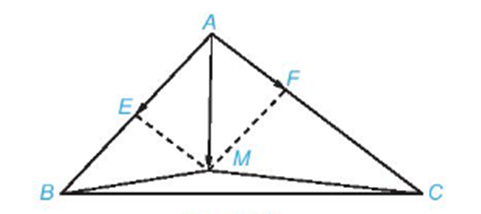
Để xác định vị trí điểm M, trước hết ta biểu thị →AM (với gốc A đã biết) theo hai vec tơ →AB,→AC.
Đẳng thức vec tơ đã cho tương đương với \(\overrightarrow {MA} + 3\left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
⇔6→MA+3→AB+2→AC=→0
⇔→AM=12→AB+13→AC.
Vì E là trung điểm của AB và F thuộc cạnh AC sao cho AF = 13AC nên →AE=12→AB và →AF=13→AC.
Vì vậy →AM=→AE+→AF.
Suy ra M là đỉnh thứ tư của hình bình hành EAFM.
Câu 10:
Biết rằng hai vectơ →avà →b không cùng phương nhưng hai vectơ 5x→a+4→b và (3x−2)→a−2→bcùng phương. Khi đó giá trị của x bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Vectơ 5x→a+4→b và (3x−2)→a−2→bcùng phương khi 5x = - 2(3x – 2)
⇔ 5x = -6x + 4
⇔ 11x = 4
⇔ x = 411.
Vậy x = 411.
Câu 11:
Chất điểm A chịu tác động của ba lực →F1,→F2,→F3như hình vẽ và ở trạng thái cân bằng (tức là →F1+→F2+→F3=→0). Tính độ lớn của các lực →F2,→F3, biết →F1 có độ lớn là 20N.
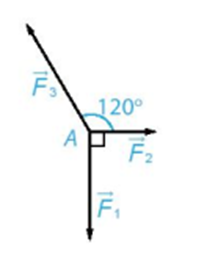
 Xem đáp án
Xem đáp án
Đáp án đúng là A
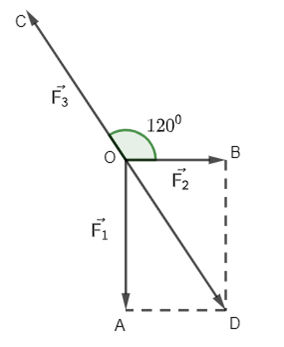
Ta có: →F1+→F2+→F3=→0
⇔→F1+→F2=−→F3
Mà →F1+→F2=→OA+→OB=→OD (OBDA là hình bình hành)
⇒→OD=−→F3
⇒Hai vecto →OD và →F3 là hai vecto đối nhau
⇒|→OD|=|−→F3| và ^BOD=600.
Ta lại có: →BD=→F1
Xét ΔOBD, có:
OB=BDtan600=20√3(N)⇒|→F2|=20√3N.
OD=BDsin600=40√33(N)⇒|→F3|=40√33N.
Vậy độ lớn vecto →F2,→F3 lần lượt là 20√3N,40√33N.
Câu 12:
Cho hình vuông ABCD có cạnh AB = 2 và giao điểm các đường chéo là H. Tính độ dài của vectơ →AB+2→AH.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì ABCD là hình bình hành nên AH = HC = 12AC. Khi đó →AH=12→AC
Ta có: \(\overrightarrow {AB} + 2\overrightarrow {AH} = \overrightarrow {AB} + 2.\frac{1}{2}.\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AC} \)
Gọi M là trung điểm của DC
⇒→AB+→AC=2→AM
⇒→AB+2→AH=2→AM
⇒|→AB+2→AH|=2|→AM|
Xét tam giác ADM vuông tại M, có:
AM2 = AD2 + DM2 = 22 + (22)2= 5 (định lí Py – ta – go)
⇔ AM = √5.
Vậy |→AB+2→AH|=√5.
Câu 13:
Cho tứ giác ABCD. Gọi M là trung điểm của cạnh AB, CD. Đẳng thức nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
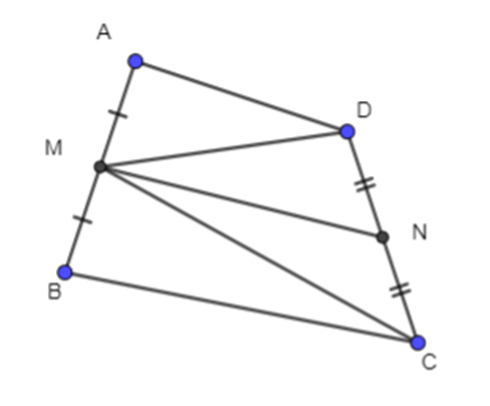
Ta có →BC+→AD=→BM+→MC+→AM+→MD
=(→BM+→AM)+(→MC+→MD)
=→0+2→MN
=2→MN
Vậy →BC+→AD=2→MN.
Câu 14:
Cho hai vectơ →a và →b khác vec tơ – không. Hai vec tơ nào dưới đây cùng phương?
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có: −6(16→a−→b)=−→a+→b. Do đó vectơ 16→a−→b và −→a+6→b cùng phương.
Câu 15:
Cho hình vẽ sau:

Phát biểu nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
+) Ta có hai vectơ →MP và →MN cùng hướng và MP=45MN. Suy ra →MP=45→MN hay 5→MP=4→MN. Do đó A đúng.
+) Ta có hai vectơ →PM và →PN ngược hướng và PM = 4PN. Suy ra →PM=−4→PN. Do đó B sai.
+) Ta có hai vectơ →PN và →MN cùng hướng và PN=15MN. Suy ra →PN=15→MN. Do đó D sai.
