Đề thi Toán lớp 6 Giữa kì 1 có đáp án
Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 6)
-
656 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Các số tự nhiên lớn hơn 2 và nhỏ hơn hoặc bằng 8 là: 3, 4, 5, 6, 7, 8.
Để viết tập hợp M các số tự nhiên lớn hơn 2 và nhỏ hơn hoặc bằng 8 ta có thể viết bằng 2 cách:
+ Liệt kê các phần tử của tập hợp: M = {3; 4; 5; 6; 7; 8};
+ Chỉ ra dấu hiệu đặc trưng: M = {x ∈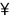 
| 2 < x ≤ 8}.
Vậy chỉ có đáp án B là đúng.
Chọn đáp án B.
Câu 2:
Xem đáp án
Thứ tự thực hiện phép tính đối với biểu thức không chứa dấu ngoặc là:
Lũy thừa → nhân, chia → cộng, trừ
Chọn đáp án B.
Câu 3:
Xem đáp án
Ư(8) = {1; 2; 4; 8}
Tập hợp X các số tự nhiên nhỏ hơn 6 và là ước của 8 là: X = {1; 2; 4}
Chọn đáp án C.
Câu 4:
Xem đáp án
Các số nguyên tố trong các số trên là: 2; 13; 19; 31 vì các số này đều lớn hơn 1 và mỗi số chỉ có đúng 2 ước là 1 và chính nó.
Chọn đáp án B.
Câu 5:
Xem đáp án
Tam giác đều là tam giác có ba cạnh bằng nhau, ba góc bằng nhau và bằng 60°.
Chọn đáp án A.
Câu 6:
Xem đáp án
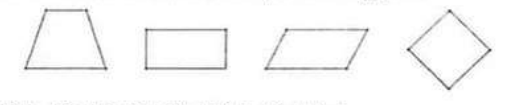
Theo thứ tự từ trái sang phải có: Hình thang cân, hình chữ nhật, hình bình hành, hình thoi.
Chọn đáp án C.
Câu 7:
Xem đáp án
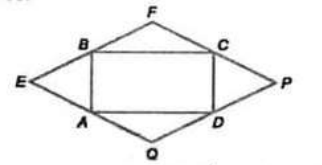
Trong hình vẽ có 2 tam giác đều đó là: ABE và CDP.
Chọn đáp án A.
Câu 8:
Xem đáp án
Hình vuông ban đầu có cạnh là a (đvđd, a >0)
Diện tích hình vuông là: a.a
Khi cạnh tăng lên 3 lần hay cạnh là 3a thì diện tích hình vuông là: 3a.3a = 9.a.a
Vậy diện tích hình vuông tăng gấp 9 lần.
Chọn đáp án D.
Câu 9:
a) 467 + 238 + 533 + 762 + 3465
b) 57.115 – 57.15 + 57
c) 32.{450 : [200 – (27 + 23)5: 504]}
Xem đáp án
Lời giải:
a) 467 + 238 + 533 + 762 + 3465
= (467 + 533) + (238 + 762) + 3465
= 1000 + 1000 + 3465
= 5465
b) 57.115 – 57.15 + 57
= 57.(115 – 15) + 57
= 57.100 + 57
= 5700 + 57
= 5757
c) 32.{450 : [200 – (27 + 23)5: 504]}
= 32.[450 : (200 – 505: 504)]
= 32.[450 : (200 – 50)]
= 32.(450 : 150)
= 32. 3
= 33= 27.
Câu 10:
Tìm số tự nhiên x, y biết:
a) x – 36 : 18 = 12;
b) 2.(x – 51) = 2 . 22+ 20;
c) x ∈ Ư(30) và x >10;
d) chia hết cho 2; 5 và 9.
Xem đáp án
Lời giải:
a) x – 36 : 18 = 12
x – 2 = 12
x = 12 + 2
x = 14
Vậy x = 14.
b) 2.(x – 51) = 2 . 23+ 20
2.(x – 51) = 2 . 8 + 20
2.(x – 51) = 36
x – 51 = 36 : 2
x – 51 = 18
x = 18 + 51
x = 69
Vậy x = 69.
c) x ∈ Ư(30) và x >10
x ∈ Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
Vì x >10 nên x ∈ {15; 30}.
d) chia hết cho 2; 5 và 9.
Để chia hết cho 2 và 5 thì số tận cùng phải là 0
Do đó y = 0
Ta có: 3 + 8 + x + 0 = 11 + x
Để chia hết cho 9 thì (11 + x) phải chia hết cho 9
Ta thấy x = 7 thỏa mãn (vì 11 + 7 = 18 chia hết cho 9)
Vậy số cần tìm để chia hết cho 2; 5 và 9 là 3870.
Câu 11:
a) Tình diện tích mảnh vườn và tổng diện tích bày tiểu cảnh và thư giãn.
b) Người chủ vườn đã thuê người về trồng hoa với chi phí mỗi mét vuông là 80 000 đồng. Tính số tiền công phải chi trả cho việc trồng hoa.
Xem đáp án
Lời giải:
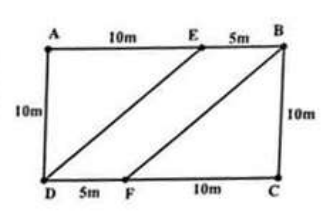
a) Diện tích mảnh vườn hình chữ nhật là:
15 . 10 = 150 (m2)
Hình bình hành EBFD có cạnh DF = 5 m và chiều cao ứng với cạnh DF chính bằng chiều rộng hình chữ nhật ABCD và bằng 10 m.
Diện tích hình bình hành EBFD hay chính là diện tích phần vườn trồng hoa là:
5 . 10 = 50 (m2)
Vậy diện tích bày tiểu cảnh và thư giãn là:
150 – 50 = 100 (m2)
b) Vì chi phí trồng hoa cho mỗi mét vuông là 80 000 đồng.
Nên số tiền công phải chi trả cho việc trồng hoa là:
50 . 80 000 = 4 000 000 (đồng).
Câu 12:
Tìm số dư khi chia tổng A cho 13.
Xem đáp án
Lời giải:
A = 3 + 32+ 33+ … + 32021
A + 1 = 1 + 3 + 32+ 33+ … + 32019+ 32020+ 32021
= (1 + 3 + 32) + (33 + 34+ 35) + … + (32019+ 32020+ 32021)
= 13 + 33.(1 + 3 + 32) + … + 32019.(1 + 3 + 32)
= 13 + 33.13 + … + 32019.13
= 13.(1 + 33+ … + 32019)
Vì 13 ⁝ 13 nên 13.(1 + 33+ … + 32019) ⁝ 13 (tính chất chia hết của một tích)
Do đó A + 1 chia hết cho 13
Vậy số dư khi A : 13 là 12.