Giải SGK Toán 8 (Kết nối tri thức): Luyện tập chung trang 88

Giải SGK Toán lớp 8: Luyện tập chung trang 88

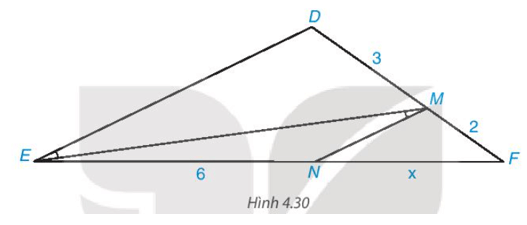
Bài 4.13 trang 88 Toán 8 Tập 1: Tìm độ dài x trong Hình 4.30

Lời giải:

Trong Hình 4.30 có $\widehat{DEM}=\widehat{EMN}$ mà hai góc này ở vị trí so le trong nên MN // DE.

Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:

$\frac{MF}{MD}=\frac{NF}{NE}$ hay $\frac{2}{3}=\frac{x}{6}$.

Suy ra $x=\frac{2.6}{3}=4$ (đvđd).

Vậy x = 4 (đvđd)

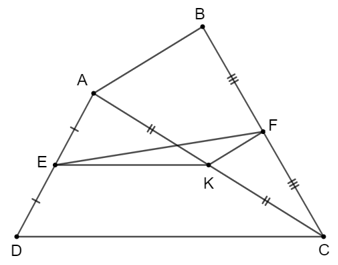
Bài 4.14 trang 88 Toán 8 Tập 1: Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.

a) Chứng minh EK // CD, FK // AB.

b) So sánh EF và $\frac{1}{2}(AB+CD)$.

Lời giải:

a) Vì E, K lần lượt là trung điểm của AD, AC nên EK là đường trung bình của tam giác ACD suy ra EK // CD.

Vì K, F lần lượt là trung điểm của AC, BC nên KF là đường trung bình của tam giác ABC suy ra KF // AB.

Vậy EK // CD, FK // AB.

b) Vì EK là đường trung bình của tam giác ACD nên $EK=\frac{1}{2}CD$ ;

Vì KF là đường trung bình của tam giác ABC nên $KF=\frac{1}{2}AB$ .

Do đó $EK+KF=\frac{1}{2}(AB+CD)$           (1)

Áp dụng bất đẳng thức tam giác vào tam giác KEF, ta có: EF < EK + KF      (2)

Từ (1) và (2) ta suy ra $EF<\frac{1}{2}(AB+CD)$.

Bài 4.15 trang 88 Toán 8 Tập 1: Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng $\frac{AC}{AB}=\frac{EC}{EA}$

Lời giải:

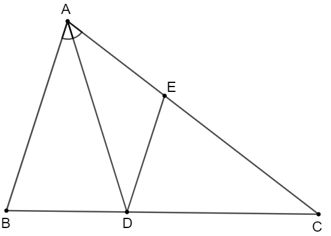
Theo đề bài, AD là tia phân giác của $\widehat{BAC}$, áp dụng tính chất đường phân giác vào tam giác ABC, ta có: $\frac{AC}{AB}=\frac{DC}{DB}$             (1)

Đường thẳng qua D song song với AB cắt AC tại E hay DE // AB, áp dụng định lí Thalès vào tam giác ABC, ta có: $\frac{DC}{DB}=\frac{EC}{EA}$                    (2)

Từ (1) và (2) suy ra $\frac{AC}{AB}=\frac{EC}{EA}$ (đpcm).

Bài 4.16 trang 88 Toán 8 Tập 1: Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D.

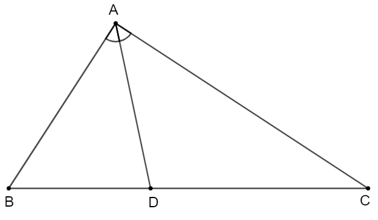
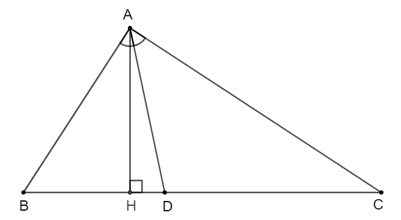
a) Tính độ dài đoạn thẳng DB và DC.

b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Lời giải:

a)

Áp dụng tính chất đường phân giác, ta có:

$\frac{DB}{DC}=\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}$.

Suy ra $\frac{DB}{3}=\frac{DC}{4}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{DB}{3}=\frac{DC}{4}=\frac{DB+DC}{3+4}=\frac{BC}{7}=\frac{25}{7}$.

Do đó, $DB=\frac{25.3}{7}=\frac{75}{7}$ (cm); $DC=\frac{25.4}{7}=\frac{100}{7}$ (cm).

Vậy $DB=\frac{75}{7}$ cm; $DC=\frac{100}{7}$cm.

b) Hai tam giác ABD và ACD có chung đường cao kẻ từ đỉnh A đến cạnh BC, ta gọi đường cao đó là AH.

Ta có: $S_{ABD}=\frac{1}{2}AH.DB;S_{ADC}=\frac{1}{2}AH.DC$ .

Suy ra $\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{DB}{DC}=\frac{3}{4}$ .

Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng $\frac{3}{4}$.

Bài 4.17 trang 88 Toán 8 Tập 1: Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM² = MN.MK.

Lời giải:

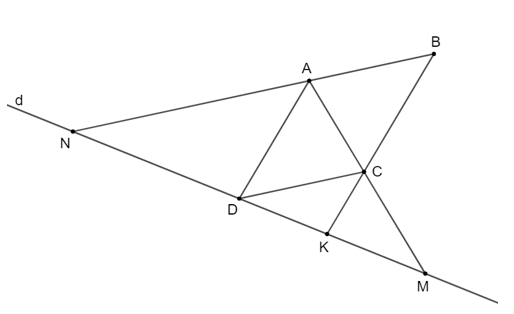
Vì ABCD là hình bình hành nên AB // CD, AD // BC suy ra AN // cD, ad // ck.

Áp dụng định lí Thalès vào tam giác AMN có AN // CD, ta được:

$\frac{DM}{MN}=\frac{CM}{AM}$           (1)

Áp dụng định lí Thalès vào tam giác ADM có CK // AD, ta được:

$\frac{MK}{DM}=\frac{CM}{AM}$           (2)

Từ (1) và (2) suy ra: $\frac{DM}{MN}=\frac{MK}{DM}=\frac{CM}{AM}$ .

Do đó DM² = MN . MK(đpcm).

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác: