Giải SGK Toán 8 (Chân trời sáng tạo) Bài 2: Tứ giác

Tổng quan

Hỏi đáp (15)

Chủ đề (8)

1900.edu.vn xin giới thiệu giải bài tập Toán 8 Bài 2 (Chân trời sáng tạo): Tứ giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 2. Mời các bạn đón xem:

Giải Toán 8 Bài 2: Tứ giác

Giải Toán 8 trang 63 Tập 1

Khởi động trang 63 Toán 8 Tập 1: Hình màu xanh bên được trích ra từ bản đồ được gọi là Tứ giác Long Xuyên. Em hãy cho biết:

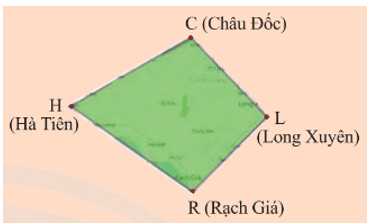
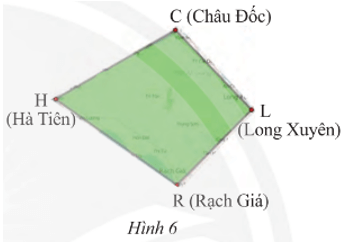
‒ Hình này được tạo bởi mấy đoạn thẳng?

‒ Các đoạn thẳng này nối các địa điểm nào?

Lời giải:

‒ Hình trên được tạo bởi 4 đoạn thẳng (CH, HR, RL, LC).

‒ Các đoạn thẳng này nối các địa điểm C (Châu Đốc), H (Hà Tiên), Q (Rạch Giá), L (Long Xuyên).

1. Tứ giác

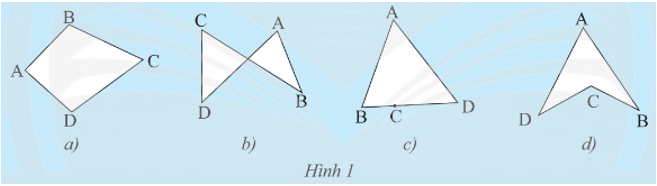
Khám phá 1 trang 63 Toán 8 Tập 1: Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?

Lời giải:

Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1, hình a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.

Khám phá 2 trang 64 Toán 8 Tập 1: Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của các cạnh còn lại của tứ giác đối với mỗi đường thẳng đã vẽ.

Lời giải:

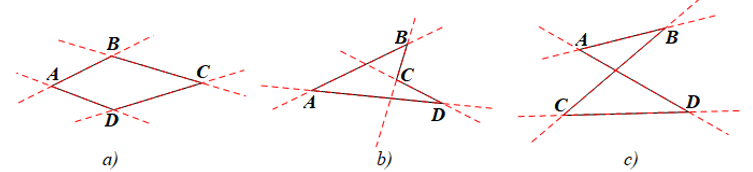
Khám phá 2 trang 64 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Ta vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác như hình vẽ dưới đây:

Nhận xét:

• Hình a): các cạnh còn lại của tứ giác luôn nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

• Hình b): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.

• Hình c): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.

Giải Toán 8 trang 65 Tập 1

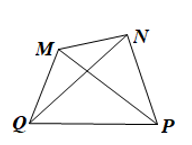
Thực hành 1 trang 65 Toán 8 Tập 1: Vẽ tứ giác MNPQ và tìm:

‒ Hai đỉnh đối nhau;

‒ Hai đường chéo;

‒ Hai cạnh đối nhau.

Lời giải:

Thực hành 1 trang 65 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Trong tứ giác MNPQ có:

‒ Hai đỉnh đối nhau: M và P; N và Q;

‒ Hai đường chéo: MP và NQ;

‒ Hai cạnh đối nhau: MN và PQ; MQ và NP.

Vận dụng 1 trang 65 Toán 8 Tập 1: Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6).

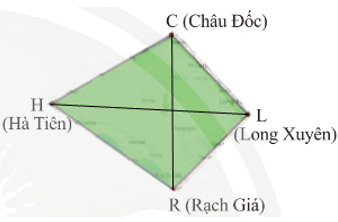
Lời giải:

Vận dụng 1 trang 65 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Trong tứ giác Long Xuyên CHRL có:

• Các đỉnh: C, H, R, L;

• Các cạnh: CH, HR, RL, LC;

• Các đường chéo: CR và HL.

2. Tổng các góc của một tứ giác

Khám phá 3 trang 65 Toán 8 Tập 1: Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?

Lời giải:

• Xét DACB có: $\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (định lí tổng ba góc trong một tam giác).

Xét DACD có: $\hat{C A D} + \hat{A C D} + \hat{A D C} = 180 °$ (định lí tổng ba góc trong một tam giác).

Do đó $\hat{B A C} + \hat{A B C} + \hat{A C B} + \hat{C A D} + \hat{A C D} + \hat{A D C} = 180 ° + 180 ° = 360 °$ .

Vậy tổng các góc của tam giác ACB và tam giác ACD bằng 360°.

• Ta có: $\hat{B A C} + \hat{A B C} + \hat{A C B} + \hat{C A D} + \hat{A C D} + \hat{A D C} = 360 °$

Suy ra $(\hat{B A C} + \hat{C A D}) + \hat{A B C} + (\hat{A C B} + \hat{A C D}) + \hat{A D C} = 360 °$

Hay $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ .

Vậy tổng các góc của tứ giác ABCD bằng 360°.

Giải Toán 8 trang 66 Tập 1

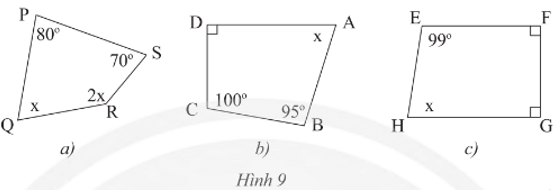
Thực hành 2 trang 66 Toán 8 Tập 1: Tìm x trong mỗi tứ giác sau:

Lời giải:

• Hình 9a):

Xét tứ giác PQRS có: 80° + 70° + 2x + x = 360° (định lí tổng các góc của một tứ giác)

Suy ra 3x = 360° – (80° + 70°) = 210°

Do đó x = 70°.

• Hình 9b):

Xét tứ giác ABCD có: x + 95° + 100° + 90° = 360° (định lí tổng các góc của một tứ giác)

Suy ra x = 360° – (95° + 100° + 90°) = 75°.

• Hình 9c):

Xét tứ giác EFGH có: 99° + 90° + 90° + x = 360° (định lí tổng các góc của một tứ giác)

Suy ra x = 360° – (99° + 90° + 90°) = 81°.

Vận dụng 2 trang 66 Toán 8 Tập 1: Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Lời giải:

Vận dụng 2 trang 66 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

Suy ra $\hat{B} = \hat{D}$ (hai góc tương ứng).

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $130 ° + \hat{B} + 60 ° + \hat{B} = 360 °$

Hay $2 \hat{B} = 360 ° - (130 ° + 60 °) = 170 °$ .

Do đó $\hat{B} = 85 °$ .

Vậy $\hat{B} = \hat{D} = 85 °$ .

Bài tập

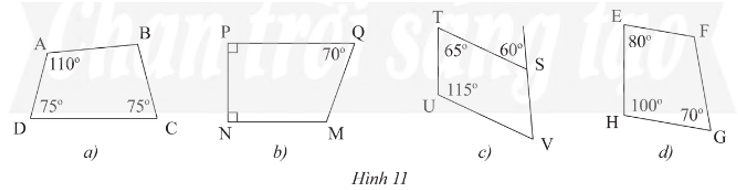
Bài 1 trang 66 Toán 8 Tập 1: Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Lời giải:

• Hình 11a):

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{B} = 360 ° - (\hat{A} + \hat{C} + \hat{D})$

Hay $\hat{B} = 360 ° - (110 ° + 75 ° + 75 °) = 100 °$ .

• Hình 11b):

Xét tứ giác MNPQ có: $\hat{M} + \hat{N} + \hat{P} + \hat{Q} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{M} = 360 ° - (\hat{N} + \hat{P} + \hat{Q})$

Hay $\hat{M} = 360 ° - (90 ° + 90 ° + 70 °) = 110 °$ .

• Hình 11c):

Ta có $\hat{T S V} = 180 ° - 60 ° = 120 °$ (do $\hat{T S V}$ kề bù với góc có số đo bằng 60°)

Xét tứ giác STUV có: $\hat{T S V} + \hat{T} + \hat{U} + \hat{V} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{V} = 360 ° - (\hat{T S V} + \hat{T} + \hat{U})$

Hay $\hat{V} = 360 ° - (120 ° + 65 ° + 115 °) = 60 °$ .

• Hình 11d):

Xét tứ giác EFGH có: $\hat{E} + \hat{F} + \hat{G} + \hat{H} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{F} = 360 ° - (\hat{E} + \hat{G} + \hat{H})$

Hay $\hat{F} = 360 ° - (80 ° + 70 ° + 100 °) = 110 °$ .

Bài 2 trang 66 Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.

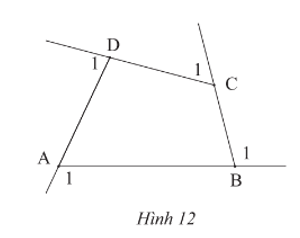
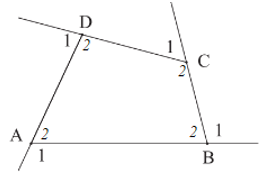
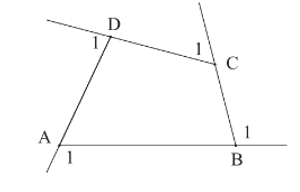
Hãy tính tổng số đo bốn góc ngoài của tứ giác ABCD ở Hình 12.

Lời giải:

Bài 2 trang 66 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Xét tứ giác ABCD có: ${\hat{A}}_{2} + {\hat{B}}_{2} + {\hat{C}}_{2} + {\hat{D}}_{2} = 360 °$ (định lí tổng các góc của một tứ giác)

Mặt khác: ${\hat{A}}_{1} + {\hat{A}}_{2} = 180 °$ (hai góc kề bù)

Tương tự: ${\hat{B}}_{1} + {\hat{B}}_{2} = 180 °; {\hat{C}}_{1} + {\hat{C}}_{2} = 180 °; {\hat{D}}_{1} + {\hat{D}}_{2} = 180 °$

Suy ra

$({\hat{A}}_{1} + {\hat{A}}_{2}) + ({\hat{B}}_{1} + {\hat{B}}_{2}) + ({\hat{C}}_{1} + {\hat{C}}_{2}) + ({\hat{D}}_{1} + {\hat{D}}_{2}) = 180 ° + 180 ° + 180 ° + 180 °$

Hay ${\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1} + {\hat{D}}_{1} + ({\hat{A}}_{2} + {\hat{B}}_{2} + {\hat{C}}_{2} + {\hat{D}}_{2}) = 720 °$

Do đó ${\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1} + {\hat{D}}_{1} + 360 ° = 720 °$

Nên ${\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1} + {\hat{D}}_{1} = 720 ° - 360 ° = 360 °$ .

Vậy tổng số đo bốn góc ngoài ${\hat{A}}_{1}, {\hat{B}}_{1}, {\hat{C}}_{1}, {\hat{D}}_{1}$ của tứ giác ABCD bằng 360°.

Giải Toán 8 trang 67 Tập 1

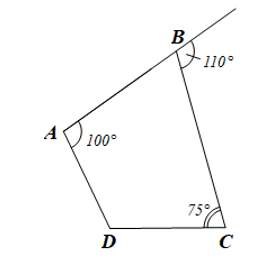
Bài 3 trang 67 Toán 8 Tập 1: Tứ giác ABCD có $\hat{A} = 100 °$ , góc ngoài tại đỉnh B bằng 110°, $\hat{C} = 75 °$ . Tính số đo góc D

Lời giải:

Bài 3 trang 67 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Do góc ngoài tại đỉnh B có số đo bằng 110° nên $\hat{A B C} = 180 ° - 110 ° = 70 °$ .

Xét tứ giác ABCD có: $\hat{A} + \hat{A B C} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{D} = 360 ° - (\hat{A} + \hat{A B C} + \hat{C})$

Do đó $\hat{D} = 360 ° - (100 ° + 70 ° + 75 °) = 115 °$ .

Bài 4 trang 67 Toán 8 Tập 1: Tứ giác ABCD có góc ngoài tại đỉnh A bằng 65°, góc ngoài tại đỉnh B bằng 100°, góc ngoài tại đỉnh C bằng 60°. Tính số đo góc ngoài tại đỉnh D.

Lời giải:

Gọi ${\hat{A}}_{1}, {\hat{B}}_{1}, {\hat{C}}_{1}, {\hat{D}}_{1}$ lần lượt là các góc ngoài tại đỉnh A, đỉnh B, đỉnh C, đỉnh D (hình vẽ).

Bài 4 trang 67 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Áp dụng kết quả của Bài tập 2, trang 66 Sách giáo khoa Toán 8, Tập một cho tứ giác ABCD ta có: ${\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1} + {\hat{D}}_{1} = 360 °$

Suy ra ${\hat{D}}_{1} = 360 ° - ({\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1})$

Do đó ${\hat{D}}_{1} = 360 ° - (65 ° + 100 ° + 60 °) = 135 °$

Vậy góc ngoài tại đỉnh D có số đo bằng 135°.

Bài 5 trang 67 Toán 8 Tập 1: Tứ giác ABCD có số đo $\hat{A} = x, \hat{B} = 2 x, \hat{C} = 3 x, \hat{D} = 4 x$ . Tính số đo các góc của tứ giác đó

Lời giải:

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra x + 2x + 3x + 4x = 360°

Hay 10x = 360°

Do đó x = 36°.

Khi đó: $\hat{A} = 36 °; \hat{B} = 2.36 ° = 72 °; \hat{C} = 3.36 ° = 108 °; \hat{D} = 4.36 ° = 144 °$ .

Vậy $\hat{A} = 36 °; \hat{B} = 72 °; \hat{C} = 108 °; \hat{D} = 144 °$ .

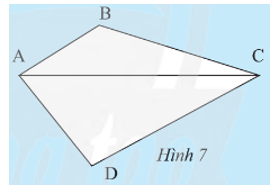
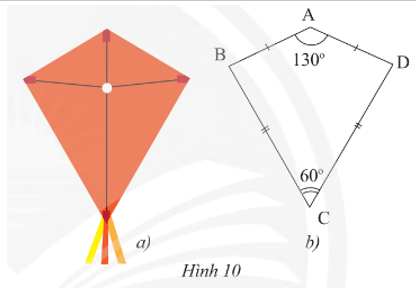
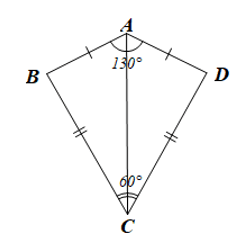
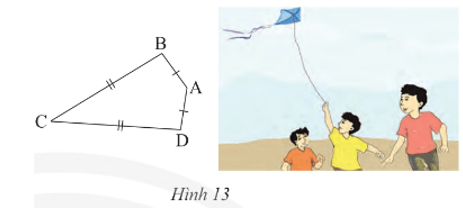
Bài 6 trang 67 Toán 8 Tập 1: Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của BD.

b) Cho biết $\hat{B} = 95 °$ , $\hat{C} = 35 °$ . Tính $\hat{A}$ và $\hat{D}$ .

Lời giải:

Bài 6 trang 67 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD.

Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD.

Do đó AC là đường trung trực của đoạn thẳng BD.

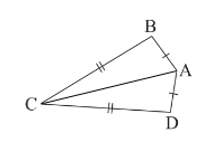
b) Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

Suy ra $\hat{B} = \hat{D}$ (hai góc tương ứng).

Mà $\hat{B} = 95 °$ nên $\hat{D} = 95 °$ .

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{A} = 360 ° - (\hat{B} + \hat{C} + \hat{D})$

Do đó $\hat{A} = 360 ° - (95 ° + 35 ° + 95 °) = 135 °$ .

Vậy $\hat{A} = 135 °$ và $\hat{D} = 95 °$ .

Bài 7 trang 67 Toán 8 Tập 1: Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.

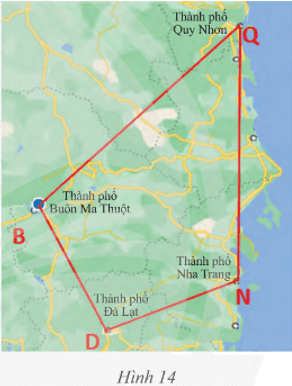
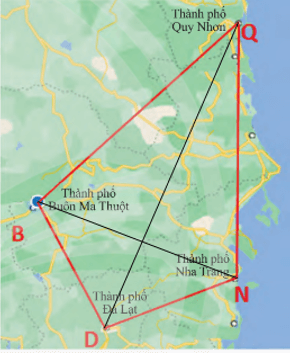
a) Tìm các cạnh kề và cạnh đối của cạnh BD.

b) Tìm các đường chéo của tứ giác.

Lời giải:

Bài 7 trang 67 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

a) Tứ giác BDNQ có:

• Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB;

• Các cạnh đối: BD và NQ; DN và BQ.

b) Tứ giác BDNQ có các đường chéo BN và DQ.

Xem thêm lời giải bài tập SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Định lí Pythagore

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông

Câu hỏi liên quan

Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”

Do đó AC là đường trung trực của đoạn thẳng BD.
Xem thêm

Tứ giác ABCD có A ̂=100°, góc ngoài tại đỉnh B bằng 110°

Do đó D ̂=360°-(100°+70°+75°)=115°.
Xem thêm

Tứ giác ABCD có số đo A ̂=x,B ̂=2.x,C ̂=3.x,D ̂=4.x

Vậy A ̂=36°;B ̂=72°;C ̂=108°;D ̂=144°.
Xem thêm

Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6)

• Các đỉnh: C, H, R, L;
Xem thêm

Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt

• Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB;
Xem thêm

Vẽ tứ giác MNPQ và tìm: Hai đỉnh đối nhau

‒ Hai đỉnh đối nhau: M và P; N và Q;
Xem thêm

Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA sau đây

Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1, hình a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.
Xem thêm

Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b

Vậy B ̂=D ̂=85°.
Xem thêm

Hình màu xanh bên được trích ra từ bản đồ được gọi là Tứ giác Long Xuyên

‒ Hình trên được tạo bởi 4 đoạn thẳng (CH, HR, RL, LC).
Xem thêm

Tìm số đo các góc chưa biết của các tứ giác trong Hình 11

Hay B ̂=360°-(110°+75°+75°)=100°.
Xem thêm

Xem tất cả hỏi đáp với chuyên mục: Tứ giác

Được cập nhật 07/10/2023 654 lượt xem

Bởi Quynh Anh

Chủ đề: giải sgk toán 8 Tứ giác

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Giải SGK Toán 8 - CTST

Giải SGK Toán 8 (Chân trời sáng tạo) Bài tập cuối chương 9

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 8 Bài tập cuối chương 9 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8. Mời các bạn đón xem:

280 10 tháng trước

Giải SGK Toán 8 - CTST

Giải SGK Toán 8 (Chân trời sáng tạo) Bài 2: Xác suất lí thuyết và xác suất thực nghiệm

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 8 Bài 2: Xác suất lí thuyết và xác suất thực nghiệm sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 2. Mời các bạn đón xem:

268 10 tháng trước

Giải SGK Toán 8 - CTST

Giải SGK Toán 8 (Chân trời sáng tạo) Bài 1: Mô tả xác suất bằng tỉ số

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 8 Bài 1: Mô tả xác suất bằng tỉ số sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 1. Mời các bạn đón xem:

413 10 tháng trước