Giải SGK Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến
Giải Toán 7 trang 37 Tập 2
Khởi động trang 37 Toán 7 Tập 2:
Có thể nhân, chia hai đa thức một biến được không?
Lời giải:
Ta có thể thực hiện nhân, chia hai đa thức một biến.
Khám phá 1 trang 37 Toán 7 Tập 2:
Hãy dùng tính chất phân phối để thực hiện phép nhân x . (2x + 3).
Lời giải:
Áp dụng tính chất phân phối, ta được:
x . (2x + 3) = x . 2x + x . 3 = 2x2 + 3x.
Thực hành 1 trang 37 Toán 7 Tập 2:
Thực hiện phép nhân (4x - 3)(2x2 + 5x - 6).
Lời giải:
Ta có: (4x - 3)(2x2 + 5x - 6)
= 4x . (2x2 + 5x - 6) + (-3) . (2x2 + 5x - 6)
= 4x . 2x2 + 4x . 5x + 4x . (-6) + (-3) . 2x2 + (-3) . 5x + (-3) . (-6)
= 8x3 + 20x2 - 24x - 6x2 - 15x + 18
= 8x3 + (20x2 - 6x2) + (-24x - 15x) + 18
= 8x3 + 14x2 - 39x + 18.
Vậy (4x - 3)(2x2 + 5x - 6) = 8x3 + 14x2 - 39x + 18.
Vận dụng 1 trang 37 Toán 7 Tập 2:
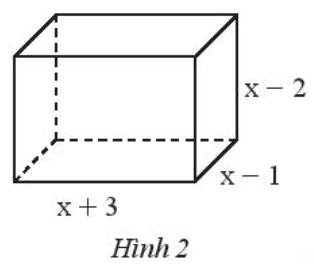
Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.
Lời giải:
Biểu thức biểu thị thể tích của hình hộp chữ nhật trên là:
(x + 3)(x - 1)(x - 2)
= [x . x + 3 . x + x . (-1) + 3 . (-1)] . (x - 2)
= (x2 + 3x - x - 3) . (x - 2)
= (x2 + 2x - 3) . (x - 2)
= x2 . x + x2 . (-2) + 2x . x + 2x . (-2) + (-3) . x + (-3) . (-2)
= x3 - 2x2 + 2x2 - 4x - 3x + 6
= x3 + (-2x2 + 2x2) + (-4x - 3x) + 6
= x3 - 7x + 6.
Vậy đa thức biểu thị thể tích của hình hộp chữ nhật trên là x3 - 7x + 6.
Giải Toán 7 trang 38 Tập 2
Khám phá 2 trang 38 Toán 7 Tập 2:
Thực hiện phép nhân (3x + 1)(x2 - 2x + 1),
rồi đoán xem (3x3 - 5x2 + x + 1) : (3x + 1) bằng đa thức nào.
Lời giải:
(3x + 1)(x2 - 2x + 1) = 3x . (x2 - 2x + 1) + 1 . (x2 - 2x + 1)
= 3x . x2 + 3x . (-2x) + 3x . 1 + x2 - 2x + 1
= 3x3 - 6x2 + 3x + x2 - 2x + 1
= 3x3 + (-6x2 + x2) + (3x - 2x) + 1
= 3x3 - 5x2 + x + 1.
Khi đó (3x3 - 5x2 + x + 1) : (3x + 1) = x2 - 2x + 1.
Thực hành 2 trang 38 Toán 7 Tập 2:
Thực hiện phép chia P(x) = 6x2 + 4x cho Q(x) = 2x.
Lời giải:
Thực hiện theo các bước như sau:
- Đặt phép chia
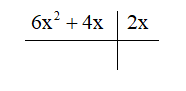
- Lấy hạng tử bậc cao nhất của đa thức P(x) chia cho hạng tử bậc cao nhất của đa thức Q(x) được 6x2 : 2x = 3x.
- Lấy P(x) trừ 3x . Q(x) ta được dư thứ nhất: 3x . 2x = 6x2.
- Lấy đa thức bị chia trừ 6x2, ta được:
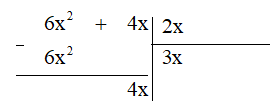
Đa thức 4x là dư thứ nhất.
- Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức Q(x) được 4x : 2x = 2.
- Lấy dư thứ nhất trừ đi 2 . Q(x) ta được dư thứ hai: 4x - 2 . 2x = 4x - 4x = 0.
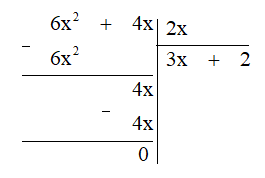
Do dư bằng 0 nên dừng phép chia.
Vậy P(x) : Q(x) = 3x + 2.
Giải Toán 7 trang 39 Tập 2
Vận dụng 2 trang 39 Toán 7 Tập 2:
Thực hiện các phép chia sau: 9x2+5x+x3x và 2x2−3x−22−x.
Lời giải:
* Xét 9x2+5x+x3x:
Ta có 9x2 + 5x + x = 9x2 + 6x.
Thực hiện đặt phép chia, ta được:
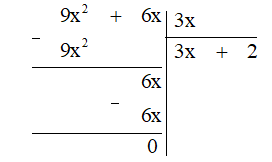
Do đó 9x2+5x+x3x = 3x + 2.
* Xét 2x2−3x−22−x:
Ta có 2 - x = -x + 2.
Thực hiện đặt phép chia ta được:
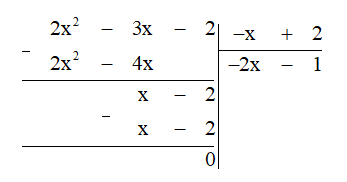
Do đó 2x2−3x−22−x = -2x - 1.
Vậy 9x2+5x+x3x = 3x + 2 và 2x2−3x−22−x = -2x - 1.
Thực hành 3 trang 39 Toán 7 Tập 2:
Thực hiện phép chia (x2 + 5x + 9) : (x + 2).
Lời giải:
Thực hiện đặt phép chia, ta được:
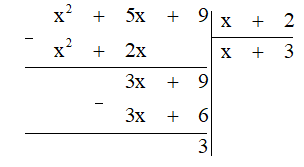
Vậy x2+5x+9x+2=x+3+3x+2.
Vận dụng 3 trang 39 Toán 7 Tập 2:
Lời giải:
Ta có công thức tính thể tích hình hộp chữ nhật là:
V = S . h (trong đó V, S và h lần lượt là thể tích, diện tích đáy và chiều cao hình hộp chữ nhật).
Khi đó, diện tích đáy hình hộp chữ nhật là:
S = V : h = (x3 + 8x2 + 19x + 12) : (x + 3) = x2 + 5x + 4 (cm2).
Vậy diện tích đáy của hình hộp chữ nhật bằng (x2 + 5x + 4) cm2.
Giải Toán 7 trang 40 Tập 2
Thực hành 4 trang 40 Toán 7 Tập 2:
Thực hiện phép tính: 15. (x2 + 1) . 5.
Lời giải:
Cách 1: Thực hiện từ trái sang phải.
15. (x2 + 1) . 5 = (15x2+15) . 5
= 15x2 . 5+15 . 5 = x2 + 1.
Cách 2: Sử dụng tính chất giao hoán và kết hợp để tính giá trị biểu thức.
15. (x2 + 1) . 5 = 15 . 5 . (x2 + 1)
= (15.5) . (x2 + 1) = x2 + 1.
Bài 1 trang 40 Toán 7 Tập 2: Thực hiện phép nhân.
c) (2x2 - 7x + 4)(-3x2 + 6x + 5).
Lời giải:
a) (4x - 3)(x + 2)
= 4x . x + 4x . 2 + (-3) . x + (-3) . 2
= 4x2 + 8x - 3x - 6
= 4x2 + (8x - 3x) - 6
= 4x2 + 5x - 6.
b) (5x + 2)(-x2 + 3x + 1)
= 5x . (-x2) + 5x . 3x + 5x . 1 + 2 . (-x2) + 2 . 3x + 2 . 1
= -5x3 + 15x2 + 5x - 2x2 + 6x + 2
= -5x3 + (15x2 - 2x2) + (5x + 6x) + 2
= -5x3 + 13x2 + 11x + 2.
c) (2x2 - 7x + 4)(-3x2 + 6x + 5)
= 2x2 . (-3x2) + 2x2 . 6x + 2x2 . 5 + (-7x) . (-3x2) + (-7x) . 6x + (-7x) . 5 + 4 . (-3x2) + 4 . 6x + 4 . 5
= -6x4 + 12x3 + 10x2 + 21x3 - 42x2 - 35x - 12x2 + 24x + 20
= -6x4 + (12x3 + 21x3) + (10x2 - 42x2 - 12x2) + (-35x + 24x) + 20
= -6x4 + 33x3 - 44x2 - 11x + 20.
Lời giải:
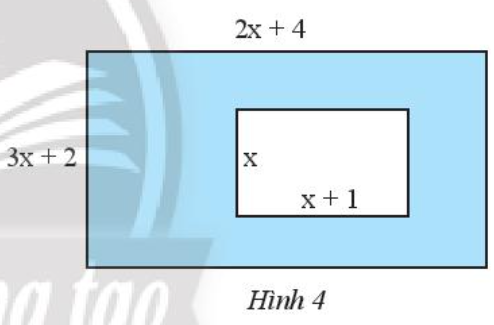
∙ Hình chữ nhật bên ngoài có chiều dài là 2x + 4 và chiều rộng là 3x + 2.
Khi đó, biểu thức biểu thị diện tích của hình chữ nhật bên ngoài là:
(2x + 4)(3x + 2) = 6x2 + 4x + 12x + 8 = 6x2 + 16x + 8.
∙ Hình chữ nhật bên trong có chiều dài là x + 1 và chiều rộng là x.
Khi đó, biểu thức biểu thị diện tích của hình chữ nhật bên trong là:
x . (x + 1) = x2 + x.
Do đó biểu thức biểu thị diện tích của phần được tô màu xanh là:
(6x2 + 16x + 8) - (x2 + x)
= 6x2 + 16x + 8 - x2 - x
= (6x2 - x2) + (16x - x) + 8
= 5x2 + 15x + 8.
Vậy biểu thức biểu thị diện tích của phần được tô màu xanh là 5x2 + 15x + 8.
Bài 3 trang 40 Toán 7 Tập 2: Thực hiện phép chia.
a) (8x6 - 4x5 + 12x4 - 20x3) : 4x3;
Lời giải:
a) Ta có (8x6 - 4x5 + 12x4 - 20x3) : 4x3
= (8x6 : 4x3) + (-4x5 : 4x3) + (12x4 : 4x3) + (-20x3) : 4x3
= 2x3 - x2 + 3x - 5
Vậy (8x6 - 4x5 + 12x4 - 20x3) : 4x3 = 2x3 - x2 + 3x - 5.
b) Thực hiện đặt phép chia, ta được:
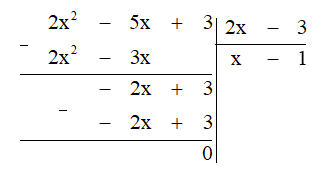
Vậy (2x2 - 5x + 3) : (2x - 3) = x - 1.
Bài 4 trang 40 Toán 7 Tập 2: Thực hiện phép chia.
b) (3x3 - 7x + 2) : (2x2 - 3).
Lời giải:
a) Thực hiện đặt phép chia ta được:
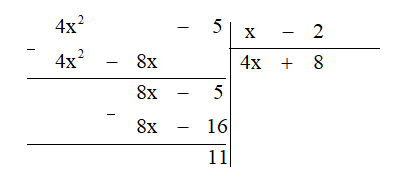
Vậy 4x2−5x−2=4x+8+11x−2.
b) Thực hiện đặt phép chia ta được:
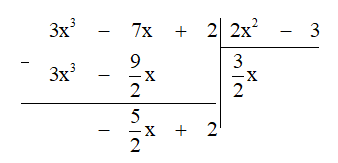
Vậy 3x3−7x+22x2−3=32x+−52x+22x2−3.
Lời giải:
Chiều dài của hình chữ nhật là:
(4y2 + 4y - 3) : (2y - 1) = 2y + 3 (cm)
Vậy chiều dài của hình chữ nhật đó bằng (2y + 3) cm.
Cho hình hộp chữ nhật có thể tích bằng (3x3 + 8x2 - 45x - 50) cm3, chiều dài bằng
(x + 5) cm và chiều cao bằng (x + 1) cm. Hãy tính chiều rộng của hình hộp chữ nhật đó.
Lời giải:
Diện tích đáy của hình hộp chữ nhật là:
(3x3 + 8x2 - 45x - 50) : (x + 1) = 3x2 + 5x – 50 (cm)
Chiều rộng của hình hộp chữ nhật là:
(3x2 + 5x – 50) : (x + 5) = 3x – 10 (cm)
Vậy chiều rộng của hình hộp chữ nhật bằng (3x - 10) cm.
Xem thêm lời giải bài tập SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Phép cộng và phép trừ đa thức một biến
Bài 5: Hoạt động thực hành và trải nghiệm. Cách tính điểm trung bình môn học kì