Giải SBT Toán 8 (Kết nối tri thức) Bài 29: Hệ số góc của đường thẳng

Sách bài tập Toán 8 Bài 29: Hệ số góc của đường thẳng

Bài tập 7.33 trang 33 SBT Toán 8 Tập 2: Tìm hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1; 2) và có hệ số góc là –3

Lời giải:

Gọi hàm số bậc nhất là y = ax + b (a ≠ 0).

Đồ thị hàm số có hệ số góc là –3 nên a = –3.

Vì đồ thị hàm số đi qua điểm (1; 2) nên ta có:

2 = a . 1 + b

2 = –3 . 1 + b

2 = –3 + b

b = 5

Vậy hàm số bậc nhất cần tìm là y = –3x + 5.

Bài tập 7.34 trang 33 SBT Toán 8 Tập 2: Tìm hàm số bậc nhất có đồ thị là đường thẳng với hệ số góc là 2 và cắt trục hoành tại điểm có hoành độ bằng –3.

Lời giải:

Gọi hàm số bậc nhất cần tìm là y = ax + b (a ≠ 0).

Hệ số góc của đồ thị hàm số là 2 nên a = 2.

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng –3 tức là đi qua điểm (–3; 0). Do đó, ta có:

0 = 2 . (–3) + b

0 = –6 + b

b = 6

Vậy đồ thị hàm số cần tìm là y = 2x + 6.

Bài tập 7.35 trang 33 SBT Toán 8 Tập 2: Hãy chỉ ra các cặp đường thẳng song song và các cặp đường thẳng cắt nhau trong các đường thẳng sau:

a) y = 2x + 1;

b) y = –3x + 1;

c) y = –3x + 2;

d) y = 2x + 2.

Lời giải:

- Ta có 2 ≠ –3 nên

+ hai đường thẳng y = 2x + 1 và y = –3x + 1 cắt nhau,

+ hai đường thẳng y = 2x + 1 và y = –3x + 2 cắt nhau,

+ hai đường thẳng y = 2x + 2 và y = –3x + 1 cắt nhau,

+ hai đường thẳng y = 2x + 2 và y = –3x + 2 cắt nhau.

- Ta có –3 = –3 và 1 ≠ 2 nên hai đường thẳng y = –3x + 1 và y = –3x + 2 song song với nhau.

- Ta có 2 = 2 và 1 ≠ 2 nên hai đường thẳng y = 2x + 1 và y = 2x + 2 song song với nhau.

Bài tập 7.36 trang 33 SBT Toán Tập 2: Cho hai hàm số y = 2x + 3m và y = (2m + 1)x – 5. Tìm các giá trị của m để đồ thị của hai hàm số là:

a) Hai đường thẳng song song;

b) Hai đường thẳng cắt nhau.

Lời giải:

a)

Để đồ thị của hai hàm số là hai đường thẳng song song thì:

2 = 2m + 1 và 3m ≠ –5

2m = 1 và m ≠$-\frac{5}{3}$

m = $\frac{1}{2}$ và m ≠ $-\frac{5}{3}$

Vậy m =$\frac{1}{2}$.

b) Để đồ thị của hai hàm số là hai đường thẳng cắt nhau thì 2 ≠ 2m + 1 hay 2m ≠ 1, tức là m ≠$\frac{1}{2}$.

Bài tập 7.37 trang 33 SBT Toán 8 Tập 2: Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y = –2x + 1 và đi qua điểm (–1; 4).

Lời giải:

Do hàm số bậc nhất cần tìm có đồ thị là đường thẳng song song với đường thẳng y = –2x + 1 nên nó có dạng y = –2x + b với b ≠ 1.

Vì đồ thị hàm số đi qua điểm (–1; 4) nên ta có:

4 = –2 . (–1) + b

4 = 2 + b

b = 2 (thỏa mãn)

Vậy hàm số cần tìm là y = – 2x + 2.

Bài tập 7.38 trang 34 SBT Toán 8 Tập 2: Người ta chứng minh được rằng hai đường thẳng y = ax + b (a ≠ 0) và y = a'x + b' (a' ≠ 0) vuông góc với nhau khi tích hai hệ số góc của chúng bằng –1, tức là khi aa' = –1. Tìm giá trị của m để đường thẳng y = (2m – 4)x + 3 (m ≠ 2) vuông góc với đường thẳng y = -1/2 + 1.

Lời giải:

Để đường thẳng y = (2m – 4)x + 3 (m ≠ 2) vuông góc với đường thẳng y =$-\frac{1}{2}x$ + 1 thì:

$\left(2m-4\right).\left(\frac{-1}{2}\right)=-1$

2m – 4 = 2

2m = 6

m = 3 (thỏa mãn).

Vậy m = 3.

Bài tập 7.39 trang 34 SBT Toán 8 Tập 2: Trên cùng mặt phẳng tọa độ Oxy cho hai đường thẳng:

(d_m): y = (1 – m)x + 2 và (d'_m): y = (m + 1)x – 3.

Tùy theo giá trị của m, xét vị trí tương đối của hai đường thẳng đã cho.

Lời giải:

TH1: 1 – m = m + 1 hay m = 0 thì:

(d_m): y = x + 2

(d'_m): y = x – 3

Do đó, (d_m­) và (d'_m) là hai đường thẳng song song với nhau.

TH2: 1 – m ≠ m + 1 hay m ≠ 0 thì hai đường thẳng cắt nhau do hệ số góc khác nhau.

Bài tập 7.40 trang 34 SBT Toán 8 Tập 2: Inch (viết tắt là in) là một đơn vị chiều dài trong hệ đo lường Mỹ. Phần đường thẳng trong hình vẽ sau mô tả sự quy đổi từ x (in) sang y (cm).

a) Tính hệ số góc của đường thẳng này.

b) Đại lượng y có tỉ lệ thuận với đại lượng x không ?

Nếu có thì hệ số tỉ lệ bằng bao nhiêu?

c) Đại lượng x có tỉ lệ thuận với đại lượng y không ?

Nếu có thì hệ số tỉ lệ bằng bao nhiêu?

Lời giải:

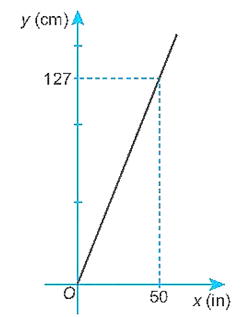
a) Từ đồ thị, ta thấy đường thẳng đi qua gốc tọa độ (và không trùng với hai trục tọa độ) nên nó là một đồ thị của một hàm số bậc nhất có dạng y = ax (a ≠ 0).

Đồ thị hàm số đi qua điểm (50; 127) nên ta có:

127 = a . 50, suy ra a =$\frac{127}{50}$= 2,54.

Do đó, hệ số góc của đường thẳng là a = 2,54.

b) Với a = 2,54, ta có y = 2,54x nên đại lượng y tỉ lệ thuận với đại lượng x và hệ số tỉ lệ là 2,54.

c) Do y = 2,54x nên $x=\frac{50}{127}y$ do đó đại lượng x cũng tỉ lệ thuận với đại lượng y và hệ số tỉ lệ là $\frac{50}{127}$ .

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: