Sách bài tập Toán 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài tập 7.25 trang 30 SBT Toán 8 Tập 2: Cho hàm số y = (1 – 2m)x + 3.
a) Với những giá trị nào của m thì hàm số đã cho là hàm số bậc nhất ?
b) Tìm m, biết đồ thị hàm số đã cho đi qua điểm (–1; 4).
c) Với giá trị m tìm được ở câu b, hãy hoàn thành bảng giá trị sau vào vở:
Lời giải:
a) Để hàm số y = (1 – 2m)x + 3 là hàm số bậc nhất thì 1 – 2m ≠ 0 hay m ≠ 12 .
b) Đồ thị hàm số đã cho đi qua điểm (–1; 4) nên ta có khi x = –1 thì y = 4.
Thay vào công thức hàm số ta có:
4 = (1 – 2m).(–1) + 3
4 = –1 + 2m + 3
2m = 2
m = 1.
Vậy m = 1.
c) Với m = 1 ta có công thức hàm số y = –x + 3.
Ta có:
Khi x = –2 thì y = –(–2) + 3 = 5;
Khi x = –1 thì y = –(–1) + 3 = 4;
Khi x = 0 thì y = –0 + 3 = 3;
Khi x = 1 thì y = –1 + 3 = 2;
Khi x = 2 thì y = –2 + 3 = 1.
Do đó, ta có bảng dưới đây
Bài tập 7.26 trang 30 SBT Toán 8 Tập 2: Vẽ đồ thị của các hàm số sau
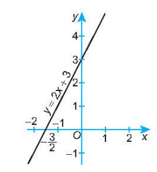
a) y = 2x + 3;
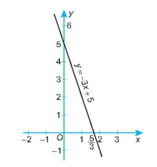
b) y = –3x + 5;
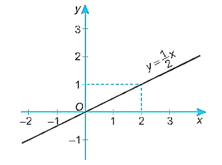
c) y = 12x;
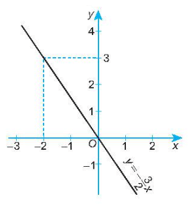
d) y =−32x.
Lời giải:
a) Khi x = 0 thì y = 3;
Khi x = thì y = 0.
Đồ thị của hàm số y = 2x + 3 là một đường thẳng đi qua hai điểm (0; 3) và .(−32;0)
b) Khi x = 0 thì y = 5;
Khi x = thì y = 0.
Đồ thị của hàm số y = –3x + 5 là một đường thẳng đi qua hai điểm (0; 5) và (53;0)
c) Khi x = 0 thì y = 0;
Khi x = 2 thì y = 1.
Đồ thị của hàm số y = 12x là đường thẳng đi qua điểm (0; 0) và (2; 1).
d) Khi x = 0 thì y = 0;
Khi x = – 2 thì y = 3.
Đồ thị của hàm số y = là đường thẳng đi qua hai điểm (0; 0) và (– 2; 3).
Bài tập 7.27 trang 30 SBT Toán 8 Tập 2: Cho ba đường thẳng
(d1): y = –2x + 1 ; (d2): y = x + 4 và (d3): y = 2mx – 3 (m ≠ 0).
a) Tìm giao điểm của hai đường thẳng (d1) và (d2).
b) Xác định giá trị của m để ba đường thẳng đã cho đồng quy.
Lời giải:
a) Gọi I(x0; y0) là giao điểm của (d1) và (d2).
Khi đó, tọa độ điểm I thỏa mãn y0 = –2x0 + 1 và y0 = x0 + 4.
Suy ra –2x0 + 1 = x0 + 4
–3x0 = 3
x0 = –1
Do đó, y0 = –1 + 4 = 3.
Vậy điểm I(–1; 3).
b)
Để ba đường thẳng đồng quy thì (d3) phải đi qua I(–1; 3) tức là khi x = –1 thì y = 3. Thay vào công thức (d3) ta có:
3 = 2m.(–1) – 3
–2m – 3 = 3
–2m = 6
m = –3
Vậy m = –3 thỏa mãn yêu cầu đề bài.
Lời giải:
Với x (giờ) lao động thì phí là: 80x (nghìn đồng)
Do đó, phí C cho một cuộc gọi dịch vụ với x (giờ) lao động là: C = 50 + 80x.
Với 3 giờ lao động tức là x = 3 thì phí dịch vụ sẽ là: C = 50 + 80.3 = 290 (nghìn đồng).
a) Viết hàm số y = f(x) biểu thị số tiền y (triệu đồng) mà anh Nam tiết kiệm được sau x (tuần).
b) Vẽ đồ thị của hàm số tìm được ở câu a. Từ đó xác định số tuần anh Nam sẽ tiết kiệm đủ tiền để mua chiếc máy tính đó.
Lời giải:
a)
Sau x (tuần) anh Nam tiết kiệm được số tiền là: 300x (nghìn đồng) = 0,3x (triệu đồng).
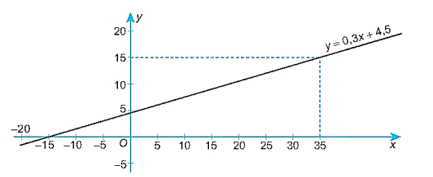
Hàm số y = f(x) biểu thị số tiền y (triệu đồng) mà anh Nam tiết kiệm được sau x (tuần) là y = 4,5 + 0,3x.
b)
Khi x = –15 thì y = 0.
Khi x = 0 thì y = 4,5.
Khi x = 35 thì y = 15.
Đồ thị hàm số y = 4,5 + 0,3x đi qua các điểm (–15; 0) ; (0; 4,5) ; (35; 15).
Từ đồ thị, ta thấy để anh Nam có đủ tiền tức là y = 15 khi đó x = 35.
Vậy anh Nam cần 35 tuần để tiết kiệm đủ tiền để mua chiếc máy tính đó.
a) Viết công thức biểu thị y (km) theo x (hải lí). Giá trị âm của x có ý nghĩa gì trong tình huống này không ? Giải thích.
b) Vẽ đồ thị của hàm số y = f(x) nhận được ở câu a.
c) Một hành trình đi biển dài 350 hải lí. Hỏi hành trình đó dài bao nhiêu kilômét ?
Lời giải:
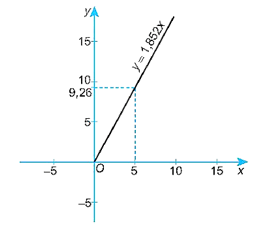
a) Vì 1 hải lí bằng 1,852 km nên ta có: y = 1,852x.
Giá trị âm của x trong trường hợp này không có ý nghĩa, vì chiều dài là một đại lượng không âm.
b)
Ta có:
Khi x = 0 thì y = 0.
Khi x = 5 thì y = 9,26.
Đồ thị của hàm số y = 1,852x (với x không âm) là một phần đường thẳng như hình bên, đi qua các điểm (0; 0) và (5; 9,26).
c) Một hành trình đi biển dài 350 hải lí. Tức là x = 350. Khi đó, hành trình dài số km là: y = 1,852 . 350 = 648,2 (km).
a) Viết hàm số bậc nhất biểu thị chi phí thuê xe mỗi ngày C (đơn vị nghìn đồng) theo x (km) đã di chuyển trong ngày.
b) Chi phí thuê xe trong ngày là bao nhiêu nếu trong ngày đó xe di chuyển quãng đường tổng cộng dài 180 km ?
Lời giải:
a)
1,5 triệu đồng = 1 500 nghìn đồng
Do thuê ô tô tính phí 1,5 triệu đồng/ngày và 10 nghìn đồng cho mỗi kilômét di chuyển nên hàm số biểu thị chi phí thuê xe mỗi ngày là: C = 1 500 + 10x (nghìn đồng).
b)
Chi phí thuê xe trong ngày nếu trong ngày đó xe di chuyển quãng đường tổng cộng dài 180 km là: C = 1500 + 10 . 180 = 3 300 (nghìn đồng).
Vậy C = 3,3 triệu đồng.
a) Tìm hàm số bậc nhất biểu thị giá trị sổ sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất tìm được ở câu a.
c) Giá trị sổ sách của mỗi chiếc xe sau 3 năm là bao nhiêu ?
d) Khi nào giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng ?
Lời giải:
a) Vì công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe sẽ giảm giá 640 : 8 = 80 (triệu đồng) nên ta có sau x năm thì mỗi chiếc xe giảm 80x (triệu đồng).
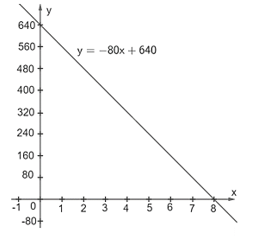
Hàm số bậc nhất biểu thị giá trị sổ sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó là: V = 640 – 80x = –80x + 640 (triệu đồng).
b) Hàm số V = –80x + 640 đi qua các điểm (0; 640) và (8; 0).
Đồ thị hàm số như hình dưới đây.
Chú ý: Vì số lớn nên ta chia khoảng cách giữa 2 trục Ox và Oy là khác nhau.
c) Giá trị sổ sách của mỗi chiếc xe sau x = 3 (năm) là:
V = –80.3 + 640 = 400 (triệu đồng).
d)
Để giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng thì:
V = 160
Hay:
–80x + 640 = 160
–80x = –480
x = 6
Vậy sau 6 năm thì giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng.
Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: