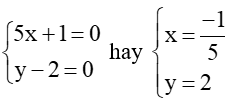Giải SBT Toán 8 (Cánh diều) Bài 3: Hằng đẳng thức đáng nhớ

Giải SBT Toán 8 Bài 3: Hằng đẳng thức đáng nhớ 

Giải SBT Toán 8 trang 14

Bài 15 trang 14 SBT Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) 9x² +12x + 4;

b) 121y² ‒ 110y + 25;

c) 36x² ‒ 96xy + 64y².

Lời giải:

a) 9x² + 12x + 4 = (3x)² + 2.3x.2 + 2² = (3x + 2)².

b) 121y² ‒ 110y + 25 = (11y)² ‒ 2.11y.2 + 5² = (11y ‒ 5)².

c) 36x² ‒ 96xy + 64y² = (6x)² ‒ 2.6x.8y + (8y)² = (6x ‒ 8y)².

Giải SBT Toán 8 trang 15

Bài 16 trang 15 SBT Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:

a) 8x³ + 12x² + 6x + 1;

b) 8x³ ‒ 36x²y + 54xy² ‒ 27y³.

Lời giải:

a) 8x³ + 12x² + 6x + 1

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³

= (2x + 1)³.

b) 8x³ ‒ 36x²y + 54xy² ‒ 27y³

= (2x)³ ‒ 3.(2x)².3y + 3.2x.(3y)³ ‒ (3y)³

= (2x ‒ 3y)³.

Bài 17 trang 15 SBT Toán 8 Tập 1: Rút gọn rồi tính giá trị của mỗi biểu thức:

a) A = (5x + 4)(5x ‒ 4) ‒ (5x + 1)² + 123 tại x = ‒1;

b) B = (2x + 1)(4x² ‒ 2x + 1) ‒ 2x(4x² ‒ 5) ‒ 11 tại $x=\frac{1}{4}$;

c) C = (4x + y)³ ‒ (4x ‒ y)³ ‒ 2y(y² +48x²) ‒ 22x + 24ytại $x=-\frac{1}{22};y=-\frac{1}{4}$.

Lời giải:

a) A = (5x + 4)(5x ‒ 4) ‒ (5x + 1)² + 123

= (5x)² – 4² – [(5x)² + 2.5x.1 + 1²] + 123

= 25x² ‒ 16 ‒ 25x² ‒ 10x ‒ 1 + 123

= (25x² ‒ 25x²) – 10x + (‒ 16 ‒ 1 + 123)

= ‒10x + 106

Thay $x=-1$ vào A, ta được: A = ‒10. (–1) + 106= 10 + 106 = 116.

Vậy giá trị của Atại $x=-1$ là A = 116.

b) B = (2x + 1)(4x² ‒ 2x + 1) ‒ 2x(4x² ‒ 5) ‒ 11

= 8x³ ‒ 4x² +2x + 4x² ‒ 2x + 1 ‒ 8x³ +10x ‒ 11

= 10x ‒ 10.

Thay $x=\frac{1}{4}$ vào B, ta được: $B=10.\frac{1}{4}-10=\frac{-15}{2}$.

Vậy giá trị của Btại $x=\frac{1}{4}$là $B=\frac{-15}{2}$.

c) C = (4x + y)³ ‒ (4x ‒ y)³ ‒ 2y(y² +48x²) ‒ 22x + 24y

= (4x)³ + 3.(4x)².y + 3.4x.y² + y³ ‒ [(4x)³ – 3.(4x)².y + 3.4x.y² – y³] ‒ 2y³ ‒ 96x²y ‒ 22x + 24y

= (4x)³ + 3.(4x)².y + 3.4x.y² + y³ – (4x)³ + 3.(4x)².y – 3.4x.y² + y³ ‒ 2y³ ‒ 96x²y ‒ 22x + 24y

= 3.(4x)².y + y³+ 3.(4x)².y + y³‒ 2y³ ‒ 96x²y ‒ 22x + 24y

= (48x²y + 48x²y ‒ 96x²y) + (y³+ y³‒ 2y³) ‒ 22x + 24y

= ‒ 22x + 24y.

Thay $x=-\frac{1}{22};y=-\frac{1}{4}$ vào C, ta được: $C=-22.\frac{-1}{22}+24.\frac{-1}{4}=-5$

Vậy giá trị của C tại $x=-\frac{1}{22};y=-\frac{1}{4}$là C = –5.

Bài 18 trang 15 SBT Toán 8 Tập 1: Tính nhanh:

a) 202²;

b) 299.301;

c) 95³ + 15.95² + 3.95.25 + 5³;

d) 9(10² + 10 + 1) + 100(98² + 392 + 2²).

Lời giải:

a) 202² = (200 + 2)²

= 200² + 2.200.2 + 2²

= 40000 + 800 + 4

= 40804.

b) 299.301 = (300 ‒ 1)(300 + 1)

= 300² ‒ 1 = 90000 ‒ 1

= 89999.

c) 95³ + 15.95² + 3.95.25 + 5³

= 95³ + 3.95².5 + 3.95.5² + 5³

= (95 + 5)³

= 100³ = 1000000.

d) 9(10² + 10 + 1) + 100(98² + 392 + 2²)

= (10 ‒ 1)(10² + 10 + 1) + 100(98² + 2.98.2 + 2²)

= 10³ ‒ 1 + 100(98 + 2)²

= 1000 ‒ 1 + 100.100²

= 999 + 1000000

= 1000999.

Bài 19 trang 15 SBT Toán 8 Tập 1: Không tính giá trị của biểu thức, hãy so sánh:

a) M = 2021.2023và N = 2022²;

b) P = 3(2² + 1)(2⁴ + 1)(2⁸ + 1) + 2và Q = (2²)⁸.

Lời giải:

a) Ta có:

M = 2021.2023 = (2022 ‒ 1)(2022 + 1) = 2022² ‒ 1

Ta thấy 2022² ‒ 1 < 2022² nên M < N.

b) Ta có:

P = 3(2² + 1)(2⁴ + 1)(2⁸ + 1) + 2

= (2² ‒ 1)(2² + 1)( 2⁴ + 1)(2⁸ + 1) + 2

= (2⁴ ‒ 1)(2⁴ + 1)(2⁸ + 1) + 2

= (2⁸ ‒ 1)(2⁸ + 1) + 2

= 2¹⁶ ‒ 1 + 2

= 2¹⁶ + 1

Q = (2²)⁸ = 2¹⁶

Ta thấy: 2¹⁶ + 1 > 2¹⁶

Vậy P > Q.

Bài 20 trang 15 SBT Toán 8 Tập 1: Tìm giá trị nhỏ nhất của mỗi biểu thức sau:

a) A = 4x² ‒ 4x + 23;

b) B = 25x² + y² + 10x ‒ 4y + 2.

Lời giải:

a) Ta có: A = 4x² ‒ 4x + 23 = (4x² ‒ 4x + 1) + 22 = (2x ‒ 1)² + 22.

Mà (2x ‒ 1)² ≥ 0 với mọi x

⇒(2x ‒ 1)² + 22 ≥ 22 với mọi x.

Vậy giá trị nhỏ nhất của A là 22 khi 2x ‒ 1 = 0 hay $x=\frac{1}{2}$.

b) Ta có: B = 25x² + y² + 10x ‒ 4y + 2

= (25x² + 10x + 1) + (y² ‒ 4y + 4) ‒ 3

= (5x + 1)² + (y ‒ 2)² ‒ 3.

Mà (5x + 1)² ≥ 0; (y ‒ 2)² ≥ 0 với mọi x và y

⇒ (5x + 1)² + (y ‒ 2)² ‒ 3 ≥ ‒3 với mọi x và y.

Vậy giá trị nhỏ nhất của B là –3 khi và chỉ khi 

Bài 21 trang 15 SBT Toán 8 Tập 1: Tìm giá trị lớn nhất của mỗi biểu thức sau:

a) C = ‒(5x ‒ 4)² + 2023;

b) D = ‒36x² + 12xy ‒ y² + 7.

Lời giải:

a) Do (5x ‒ 4)² ≥ 0 với mọi x

Suy ra ‒(5x ‒ 4)² ≤ 0 với mọi x nên ‒(5x ‒ 4)² + 2023 ≤ 2023 với mọi x.

Vậy giá trị lớn nhất của C là 2023 khi 5x ‒ 4 = 0 hay $x=\frac{4}{5}$.

b) Ta có: D = ‒36x² + 12xy ‒ y² + 7

= ‒(36x² ‒ 12xy + y²) + 7 = ‒(6x ‒ y)² + 7

Mà (6x ‒ y)² ≥ 0 với mọi x, y

Suy ra  ‒ (6x ‒ y)² ≤ 0 với mọi x và y

Do đó ‒ (6x ‒ y)² + 7 ≤ 7 với mọi x và y.

Vậy giá trị lớn nhất của D là 7 khi 6x ‒ y = 0

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến

Bài 2: Các phép tính với đa thức nhiều biến

Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử

Bài tập cuối chương 1

Bài 1: Phân thức đại số