Giải SBT Toán 8 (Kết nối tri thức) Bài 7: Lập phương của một tổng. Lập phương của một hiệu
a) x3 + 6x2 + 12x + 8;
b) 8a3 – 12a2b + 6ab2 – b3.
Lời giải:
a) x3 + 6x2 + 12x + 8
= x3 + 3.x2.2 + 3.x.22 + 23
= (x + 2)3.
b) 8a3 – 12a2b + 6ab2 – b3
= (2a)3 ‒ 3.(2a)2.b + 3.2a.b2 – b3
= (2a ‒ b)3.
Bài 2.9 trang 24 SBT Toán 8 Tập 1: Tính giá trị của mỗi biểu thức sau:
a) 8x3 + 12x2 + 6x + 1 tại x = 49,5;
b) x3 – 9x2 + 27x – 27 tại x = 103.
Lời giải:
a) Ta có:
8x3 + 12x2 + 6x + 1
= (2x)3 + 3.(2x)2.1 + 3.(2x).12 + 13
= (2x + 1)3.
Tại x = 49,5 thì (2x + 1)3 = (2 . 49,5 + 1)3 = 1003 = 1 000 000.
b) x3 – 9x2 + 27x – 27
= x3 ‒ 3.x2.3 + 3.x.32 ‒ 33
= (x – 3)3.
Tại x = 103 thì (x − 3)3 = (103 – 3)3 = 1003 = 1 000 000.
Bài 2.10 trang 24 SBT Toán 8 Tập 1: Rút gọn:
a) (x + 1)3 – (x – 1)3 − 6(x − 2)(x + 2);
b) (x − y)3 + (x + y)3 + (y − x)3 − 3xy(x + y).
Lời giải:
a) (x + 1)3 – (x – 1)3 − 6(x − 2)(x + 2)
= x3 + 3x2 + 3x + 1 ‒ (x3 ‒ 3x2 + 3x ‒ 1) ‒ 6(x2 ‒ 4)
= x3 + 3x2 + 3x + 1 ‒ x3 + 3x2 ‒ 3x + 1 ‒ 6x2 + 24
= (x3 ‒ x3) + (3x2 + 3x2 ‒ 6x2) + (3x ‒ 3x) + 1 + 1 + 24
=26.
b)(x − y)3 + (x + y)3 + (y − x)3 − 3xy(x + y)
= x3 ‒ 3x2y + 3xy2 ‒ y3 + x3 + 3x2y + 3xy2 + y3 + y3 ‒ 3xy2 + 3x2y ‒ x3 ‒ 3x2y ‒ 3xy2
= (x3 + x3 ‒ x3) + (‒ 3x2y + 3x2y + 3x2y ‒ 3x2y) + (3xy2 + 3xy2 ‒ 3xy2 ‒ 3xy2) + (‒ y3 + y3 + y3)
= x3 + y3.
Bài 2.11 trang 24 SBT Toán 8 Tập 1: Biết số tự nhiên a chia 6 dư 5. Chứng minh rằng a3 chia 6 dư 5.
Lời giải:
Vì a chia 6 dư 5 nên ta có thể viết a = 6n + 5, n ∈ ℕ. Ta có
a3 = (6n + 5)3
= (6n)3 + 3.(6n)2.5 + 3.6n.52 + 53
= 6n[(6n)2 + 3.6n.5 + 3.52] + 125.
Vì 6n[(6n)2 + 3.6n.5 + 3.52] ⋮ 6 và 125 chia 6 dư 5 nên a3 chia 6 dư 5.
Lời giải:
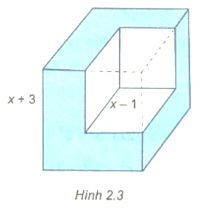
Thể tích khối lập phương có độ dài cạnh là x + 3 (cm) là: (x + 3)3 (cm3).
Thể tíchkhối lập phương có độ dài cạnh là x ‒ 1 (cm) là: (x ‒ 1)3 (cm3).
Thể tích phần còn lại là:
(x + 3)3 ‒ (x ‒ 1)3
= x3 + 3.x2.3 + 3.x.32 + 33 ‒ (x3 ‒ 3x2 + 3x ‒ 1)
= x3 + 9x2 + 27x + 27 ‒ x3 + 3x2 ‒ 3x + 1
= (x3 ‒ x3) + (9x2 + 3x2) + (27x ‒ 3x) + (27 + 1)
= 12x2 + 24x + 28.
Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:
Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Bài 8: Tổng và hiệu hai lập phương