Giải SBT Toán 8 (Kết nối tri thức): Bài tập cuối chương 2

Giải SBT Toán 8 (Kết nối tri thức) Bài tập cuối chương 2

A. Câu hỏi (Trắc nghiệm)

Chọn một phương án đúng trong mỗi câu sau:

Câu 1 trang 29 SBT Toán 8 Tập 1: Trong các đẳng thức sau, cái nào là hằng đẳng thức?

A. a(a + 1) = a + 1.

B. a² – 1 = a.

C. (a + b)(a – b) = a² + b².

D. (a + 1)(a + 2) = a² + 3a + 2.

Lời giải:

Đáp án đúng là: D

Ta có: (a + 1)(a + 2) = a² + 2a + a + 2 = a² + 3a + 2.

Do đó đẳng thức trên là một hằng đẳng thức.

Các đẳng thức còn lại, khi thay một giá trị a, b bất kì vào hai vế ta được kết quả không bằng nhau nên không phải là hằng đẳng thức.

Câu 2 trang 29 SBT Toán 8 Tập 1: Đa thức x³ – 8 được phân tích thành tích của hai đa thức

A. x − 2 và x² − 2x – 4.

B. x − 2 và x² + 2x – 4.

C. x − 2 và x² + 2x + 4.

D. x − 2 và x² – 2x + 4.

Lời giải:

Đáp án đúng là: C

Ta có: x³ – 8 = x³ ‒ 2³ = (x ‒ 2)(x² + 2x + 4).

Câu 3 trang 29 SBT Toán 8 Tập 1: Biểu thức $x^2+x+\frac{1}{4}$ viết được dưới dạng bình phương của một tổng là

A. ${\left(x+\left(-\frac{1}{2}\right)\right)}^2$.

B. ${\left(x+\frac{1}{2}\right)}^2$.

C. ${\left(2x+\frac{1}{2}\right)}^2$.

D. ${\left(\frac{1}{2}x+1\right)}^2$.

Lời giải:

Đáp án đúng là: B

Ta có: $x^2+x+\frac{1}{4}=x^2+2.x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2={\left(x+\frac{1}{2}\right)}^2$.

Câu 4 trang 29 SBT Toán 8 Tập 1: Khẳng định nào sau đây là đúng?

A. (A – B)(A² – AB + B²) = A³ – B³.

B. (A + B)(A² + AB + B²) = A³ + B³.

C. (A + B)(A² – AB + B²) = A³ – B³.

D. (A + B)(A² – AB + B²) = A³ + B³.

Lời giải:

Đáp án đúng là: D

Ta có:

•A³ + B³ = (A + B)(A² – AB + B²);

• A³ – B³ = (A – B)(A² + AB + B²).

Do đó phương án D là đúng.

Câu 5 trang 29 SBT Toán 8 Tập 1: Rút gọn biểu thức (x + 1)(x − 1) − (x + 2)(x − 2) ta được

A. 5.

B. 4.

C. 3.

D. –3.

Lời giải:

Đáp án đúng là: C

Ta có: (x + 1)(x − 1) − (x + 2)(x − 2)

= x² ‒ 1 ‒ (x² ‒ 2²)

= x² ‒ 1 ‒ x² + 4 = 3.

B. Bài tập

Bài 2.19 trang 29 SBT Toán 8 Tập 1: Tính nhanh giá trị của các biểu thức:

a) x² + 12x + 36 tại x = −1006;

b) x³ – 9x² + 27x – 27 tại x = 103.

Lời giải:

a) x² + 12x + 36 = x² + 2.x.6 + 6² = (x + 6)²

Tại x = −1006 ta có:

(‒1006 + 6)² = 1000² = 1 000 000.

b) x³ – 9x² + 27x – 27 = x³ ‒ 3.x².3 + 3.x.3² ‒ 3³ = (x ‒ 3)³

Tại x = 103 ta có:

(103 ‒ 3)³ = 100³ = 1 000 000.

Bài 2.20 trang 30 SBT Toán 8 Tập 1: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

a) (x + 1)³ – (x – 1)³ – 6x²;

b) (2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3);

c) (x – 3)(x² + 3x + 9) – (x + 2)(x² – 2x + 4).

Lời giải:

a) Cách 1:

(x + 1)³ – (x – 1)³ – 6x²

= x³ + 3x² + 3x + 1 ‒ (x³ ‒ 3x² + 3x ‒ 1) ‒ 6x²

= x³ + 3x² + 3x + 1 ‒ x³ + 3x² ‒ 3x + 1 ‒ 6x²

= (x³ ‒ x³) + (3x² + 3x² ‒ 6x²) + (3x ‒ 3x) + 1 + 1

= 2.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

Cách 2:

(x + 1)³ – (x – 1)³ – 6x²

= (x + 1 – x + 1)[(x + 1)² + (x + 1)(x – 1) + (x – 1)²] – 6x²

= 2(x² + 2x + 1 + x² – 1 + x² – 2x + 1) – 6x²

= 2(3x² + 1) – 6x²

= 6x² + 2 – 6x²

= 2.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

b) Cách 1:

(2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3)

= 4x² ‒ 12x + 9 + 4x² + 12x + 9 ‒ 2(4x² ‒ 9)

= 4x² ‒ 12x + 9 + 4x² + 12x + 9 ‒ 8x² + 18

= (4x² + 4x² ‒ 8x²) + (‒12x + 12x) + 9 + 18 = 36.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

Cách 2:

(2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3)

= (2x – 3)² – 2.(2x – 3).(2x + 3) + (2x + 3)²

= [2x – 3 – (2x + 3)]²

= (2x – 3 – 2x – 3)²

= (–6)² = 36.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

c) (x – 3)(x² + 3x + 9) – (x + 2)(x² – 2x + 4)

= (x – 3)(x² + 3x + 3²) – (x + 2)(x² – 2x + 2²)

= x³ ‒ 3³ ‒ (x³ + 2³)

= x³ ‒ 27 ‒ x³ ‒ 8

= (x³ ‒ x³) ‒ 27 ‒ 8 = ‒35.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

Bài 2.21 trang 30 SBT Toán 8 Tập 1: Không cần tính, hãy so sánh số A với số B trong các trường hợp sau:

a) A = 2021 . 2023 và B = 2022²;

b) A = 2021 . 2025 và B = 2023².

Lời giải:

a) Ta có A = 2021 . 2023

= (2022 – 1).(2022 + 1)

= 2022² – 1 < 2022².

Vậy A < B.

b) A = 2021 . 2025

= (2023 – 2)(2023 + 2)

= 2023² – 2 < 2023².

Vậy A < B.

Bài 2.22 trang 30 SBT Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x³ – y³ + 2x – 2y;

b) x² + 8xy + 16y² – 4z².

Lời giải:

a) x³ – y³ + 2x – 2y

= (x³ – y³) + (2x – 2y)

= (x − y)(x² + xy + y²) + 2(x – y)

= (x − y)(x² + xy + y² + 2);

b) x² + 8xy + 16y² – 4z²

= (x² + 8xy + 16y²) – 4z²

= (x + 4y)² – (2z)²

= (x + 4y – 2z)(x + 4y + 2z).

Bài 2.23 trang 30 SBT Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² – 3x + 2;

b) x² + 7x + 6.

Lời giải:

a) x² – 3x + 2

= x² ‒ 2x ‒ x + 2

= (x² – 2x) – (x – 2)

= x(x – 2) – (x – 2)

= (x ‒ 2)(x ‒ 1).

b) x² + 7x + 6

= x² + x + 6x + 6

= (x² + x) + (6x + 6)

= x(x + 1) + 6(x + 1)

= (x + 1)(x + 6).

Bài 2.24 trang 30 SBT Toán 8 Tập 1: Từ một miếng bìa có dạng hình tròn (H.2.4) với bán kính R (cm), người ta khoét một hình tròn ở giữa có bán kính r (cm), r < R.

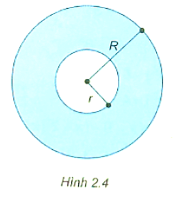
a) Viết công thức tính diện tích phần còn lại của miếng bìa.

b) Tính diện tích phần còn lại của miếng bìa biết tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm.

Lời giải:

a) Diện tích miếng bìa hình tròn có bán kính R (cm) là: πR² (cm²)

Diện tích miếng bìa hình tròn có bán kính r (cm) là: πr² (cm²)

Diện tích phần còn lại của miếng bìa là:

πR² ‒ πr² = π(R² – r²) (cm²).

b) Ta có: π(R² – r²) = π(R – r)(R + r) (*)

Do tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm nên ta có:

R + r = 10 và R ‒ r = 3

Thay vào (*) ta được: π(10 − 3)(10 + 3) = π.7.13 = 91π.

Vậy diện tích phần còn lại của miếng bìa là 91π (cm²).

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu hai lập phương

Bài 9: Phân tích đa thức thành nhân tử

Bài 10: Tứ giác

Bài 11: Hình thang cân

Bài 12: Hình bình hành