Giải SBT Toán 7 (Chân trời sáng tạo) Bài 7: Tính chất ba đường trung tuyến của tam giác

Giải Sách bài tập Toán lớp 7 Bài 7: Tính chất ba đường trung tuyến của tam giác 

Bài 1 trang 60 SBT Toán 7 Tập 2: Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh:

a) S_AMB = S_AMC;

b) S_ABG = 2S_BMG;

c) S_GAB = S_GBC = S_GAC.

Lời giải

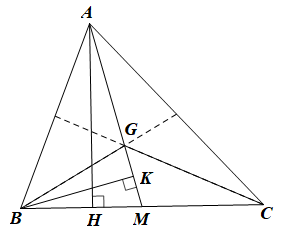
a) Vẽ đường cao AH của tam giác ABC.

Vì AM là trung tuyến của tam giác ABC nên BM = CM.

Ta có : ${\text{S}}_{\text{AMB}}=\frac{1}{2}.\text{AH.BM}$ và ${\text{S}}_{\text{AMC}}=\frac{1}{2}.\text{AH.MC}$

Hai tam giác AMB và AMC có cùng đường cao AH và có cạnh đáy bằng nhau.

Suy ra S_AMB = S_AMC.

Vậy S_AMB = S_AMC.

b) Vẽ đường cao BK của tam giác ABM.

Ta có: ${\text{S}}_{\text{ABG}}=\frac{1}{2}.\text{BK.AG}$ và ${\text{S}}_{\text{BMG}}=\frac{1}{2}.\text{BK.GM}$

Mà G là trọng tâm của tam giác ABC nên $\frac{GM}{GA}=\frac{1}{2}$ hay AG = 2GM.

Hai tam giác ABG và BMG có cùng đường cao BK và có cạnh đáy AG = 2GM.

Suy ra S_ABG = 2S_BMG.

Vậy S_ABG = 2S_BMG.

c) Ta có: S_AMB = S_AMC (chứng minh câu a) và S_AMB + S_AMC = S_ABC

Nên ${\text{S}}_{\text{AMB}}={\text{S}}_{\text{AMC}}=\frac{1}{2}{\text{S}}_{\text{ACB}}$

Vì G là trọng tâm của tam giác ABC nên AG = $\frac{1}{2}$AM.

Lại có: ${\text{S}}_{\text{GAB}}=\frac{1}{2}.\text{BK.AG}$ và ${\text{S}}_{\text{AMB}}=\frac{1}{2}.\text{BK.AM}$

Suy ra $S_{GAB}=\frac{1}{2}.\text{BK.}\frac{2}{3}\text{AM}=\frac{2}{3}{S}_{ABM}$$=\frac{2}{3}.\frac{1}{2}{S}_{ABC}=\frac{1}{3}{S}_{ABC}$

Chứng minh tương tự ta có $S_{GAC}=\frac{2}{3}{S}_{ACM}=\frac{1}{3}{S}_{ABC}$

Ta có  S_GAB + S_GAC + S_GBC = S_ABC

Mà $S_{ABG}=\frac{1}{3}{S}_{ABC}$; $S_{ACG}=\frac{1}{3}{S}_{ABC}$

Suy ra $S_{BCG}=\frac{1}{3}{S}_{ABC}$

Do đó $S_{GAB}=S_{GBC}=S_{GAC}\left(=\frac{1}{3}{S}_{ABC}\right)$

Vậy S_GAB = S_GBC = S_GAC.

Bài 2 trang 60 SBT Toán 7 Tập 2: Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác góc A. Chứng minh tam giác ABC là tam giác cân.

Lời giải

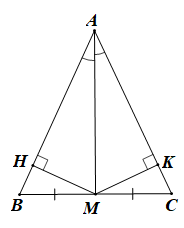
Vẽ đường cao MH của tam giác AMB và vẽ đường cao MK của tam giác AMC.

• Xét $∆$AMH và $∆$AMK có:

$\widehat{AHM}=\widehat{AKM}\left(=90°\right)$,

AM là cạnh chung,

$\widehat{HAM}=\widehat{K\text{A}M}$ (vì AM là tia phân giác của $\widehat{BAC}$).

Do đó $∆$AMH = $∆$AMK (cạnh huyền – góc nhọn).

Suy ra MH = MK (hai cạnh tương ứng).                

• Xét $∆$BMH và $∆$CMK có:

$\widehat{BHM}=\widehat{CKM}\left(=90°\right)$,

MH = MK (chứng minh trên),

BM = CM (vì AM là trung tuyến của tam giác ABC).

Do đó $∆$BMH = $∆$CMK (cạnh huyền – cạnh góc vuông).

Suy ra $\widehat{B}=\widehat{C}$ (hai góc tương ứng).

Xét tam giác ABC có $\widehat{B}=\widehat{C}$ nên tam giác ABC cân tại A.

Vậy ABC là tam giác cân tại A.

Bài 3 trang 60 SBT Toán 7 Tập 2: Cho tam giác ABC có hai trung tuyến AM và CN cắt nhau tại G

a) Biết AM = 12 cm, tính AG.

b) Biết GN = 3 cm, tính CN.

c) Tìm x biết AG = 3x – 4, GM = x.

Lời giải

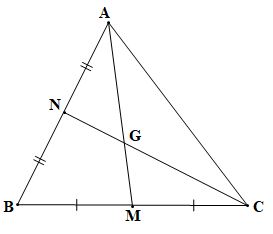
a) Vì G là trọng tâm của tam giác ABC nên AG = $\frac{2}{3}$AM.

Mà AM = 12 cm nên AG = $\frac{2}{3}$ . 12 = 8 (cm).

Vậy AM = 8 cm.

b) Vì G là trọng tâm của tam giác ABC nên $\frac{GN}{CN}=\frac{1}{3}$ hay CN = 3GN.

Mà GN = 3 cm nên CN = 3. 3 = 9 (cm).

Vậy CN = 9 cm.

c) Vì G là trọng tâm của tam giác ABC nên $\frac{GM}{GA}=\frac{1}{2}$ hay AG = 2GM.

Mà AG = 3x – 4, GM = x.

Nên 3x – 4 = 2x

Hay 3x – 2x = 4

Suy ra x = 4 (cm).

Vậy x = 4 cm.

Bài 4 trang 60 SBT Toán 7 Tập 2: Cho tam giác ABC có ba trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: $GA+GB+GC=\frac{2}{3}\left(AM+BN+CP\right)$.

Lời giải

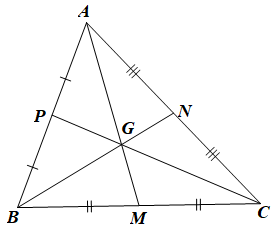
Vì $∆$ABC có ba trung tuyến AM, BN, CP đồng quy tại G nên G là trọng tâm $∆$ABC, do đó ta có: $GA=\frac{2}{3}AM,GB=\frac{2}{3}BN,GC=\frac{2}{3}CP$.

Suy ra $GA+GB+GC=\frac{2}{3}AM+\frac{2}{3}BN+\frac{2}{3}CP$$=\frac{2}{3}\left(AM+BN+CP\right)$.

Vậy $GA+GB+GC=\frac{2}{3}\left(AM+BN+CP\right)$.

Bài 5 trang 60 SBT Toán 7 Tập 2: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Vẽ AH vuông góc với BC tại H. Cho biết HB = HM. Chứng minh:

a) $∆$ABH = $∆$AMH;

b) $AG=\frac{2}{3}AB$.

Lời giải

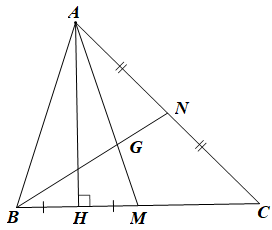
a) Xét $∆$ABH và $∆$AMH có:

$\widehat{AHB}=\widehat{AHM}\left(=90°\right)$,

Cạnh AH là cạnh chung,

HB = HM (giả thiết).

Do đó ΔABH = ΔAMH (c.g.c).

Vậy ΔABH = ΔAMH.

b) Vì $∆$ABC có hai đường trung tuyến AM và BN cắt nhau tại G nên G là trọng tâm tam giác ABC.

Suy ra $AG=\frac{2}{3}AM$.

Mặt khác ΔABH = ΔAMH (câu a) nên ta có AB = AM (hai cạnh tương ứng).

Suy ra $AG=\frac{2}{3}AB$.

Vậy $AG=\frac{2}{3}AB$.

Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài tập cuối chương 8