Giải SBT Toán 7 (Chân trời sáng tạo) Bài 6: Tính chất ba đường trung trực của tam giác

Giải Sách bài tập Toán lớp 7 Bài 6: Tính chất ba đường trung trực của tam giác

Bài 1 trang 57 SBT Toán 7 Tập 2:Điểm O trong Hình 7 có phải là giao điểm của ba đường trung trực của tam giác ABC hay không? Hãy giải thích.

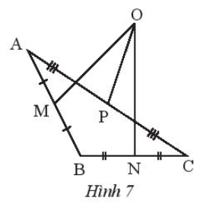
Lời giải

Vì OM không vuông góc với AB nên OM không phải đường trung trực của cạnh AB.

Suy ra O không phải là giao điểm của ba đường trung trực của tam giác ABC.

Vậy điểm O không phải là giao điểm của ba đường trung trực của tam giác ABC.

Bài 2 trang 57 SBT Toán 7 Tập 2: Cho tam giác đều ABC và điểm G như trong Hình 8. Hãy chứng minh GA = GB = GC.

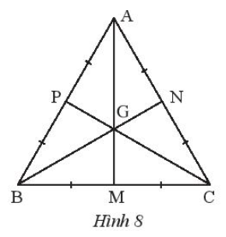
Lời giải

Vì tam giác ABC đều (giả thiết) nên AB = AC = BC.

Ta có: AB = AC, MB = MC.

Suy ra AM là trung trực của cạnh BC.

Ta có: BA = BC, NA = NC.

Suy ra BN là trung trực của cạnh AC.

Ta có: CA = CB, PA = PB.

Suy ra CP là trung trực của cạnh AB.

Xét $∆$ABC có AM, BN, CP lần lượt là trung trực của cạnh BC, AC, AB.

Mà G là giao điểm của AM, BN, CP.

Suy ra GA = GB = GC (tính chất ba đường trung trực của tam giác).

Vậy GA = GB = GC.

Bài 3 trang 58 SBT Toán 7 Tập 2: Cho tam giác ABC có góc A bằng 120°. Các đường trung trực của AB và AC lần lượt cắt BC tại M và N. Tính số đo góc MAN.

Lời giải

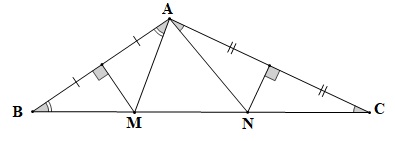
Vì M thuộc đường trung trực của AB nên MA = MB.

Do đó tam giác MAB cân tại M.

Suy ra $\widehat{MAB}=\widehat{B}$ (tính chất tam giác cân).

Vì N thuộc đường trung trực của AC nên NA = NC.

Do đó tam giác NAC cân tại N.

Suy ra $\widehat{NAC}=\widehat{C}$ (tính chất tam giác cân).

Xét $∆$ABC có: $\stackrel{︿}{\text{A}}+\stackrel{︿}{\text{B}}+\stackrel{︿}{\text{C}}=180°$ (định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}$

Do đó $\widehat{B}+\widehat{C}=180°-120°=60°$.

Ta có: $\widehat{MAN}=\widehat{BAC}-\widehat{MAB}-\widehat{NAC}$

                        $=\widehat{BAC}-\left(\widehat{MAB}+\widehat{NAC}\right)$ 

                     $=120°-\left(\widehat{B}+\widehat{C}\right)=120°-60°=60°$.

Vậy $\widehat{MAN}=60°.$

Bài 4 trang 58 SBT Toán 7 Tập 2: Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB và AC cắt nhau tại O và lần lượt cắt BC tại E và F. Hãy chứng minh:

a) $∆$EOA = $∆$EOB; $∆$FOA = $∆$FOC.

b) Chứng minh rằng AO là tia phân giác của góc EAF.

Lời giải

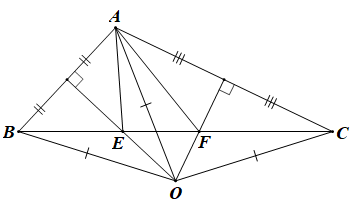
a) Vì O là giao điểm của hai đường trung trực của tam giác ABC nên OA = OB = OC.

Vì E nằm trên trung trực của AB nên ta có EA = EB.

Vì F nằm trên trung trực của AC nên ta có: FA = FC.

• Xét tam giác OEA và tam giác OEB có:

AE = BE (chứng minh trên),

OA = OB (chứng minh trên),

OE là cạnh chung.

Do đó $∆$EOA = $∆$DEB (c.c.c).

• Xét tam giác OFA và tam giác OFC có:

AF = CF (chứng minh trên),

OA = OC (chứng minh trên),

OF là cạnh chung.

Do đó $∆$FOA = $∆$FOC (c.c.c).

Vậy $∆$EOA = $∆$EOB; $∆$FOA = $∆$FOC.

b) Ta có OB = OC nên tam giác OBC cân tại O.

Suy ra $\widehat{OBE}=\widehat{OCF}$         (1)

Ta có $∆$OEA = $∆$OEB (câu a)

Suy ra $\widehat{OA\text{E}}=\widehat{OBE}$ (hai góc tương ứng) (2)

Tương tự từ $∆$OFA = $∆$OFC (câu a)

Suy ra $\widehat{OAF}=\widehat{OCF}$ (hai góc tương ứng) (3)

Từ (1), (2), (3) ta có: $\widehat{OAE}=\widehat{OAF}$ 

Suy ra AO là tia phân giác của góc EAF.

Vậy AO là tia phân giác của góc EAF.

Bài 5 trang 58 SBT Toán 7 Tập 2: Cho tam giác ABC có đường trung trực của cạnh AC đi qua đỉnh B, chứng minh tam giác ABC là tam giác cân.

Lời giải

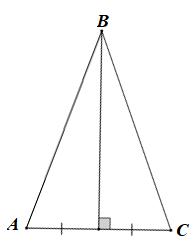
Vì B nằm trên trung trực của AC nên BA = BC.

Suy ra tam giác ABC cân tại B.

Vậy tam giác ABC là tam giác cân tại đỉnh B.

Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:

Bài 4: Đường vuông góc và đường xiên

Bài 5: Đường trung trực của một đoạn thẳng

Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác