Giải SBT Toán 7 (Chân trời sáng tạo) Bài 5: Đường trung trực của một đoạn thẳng

Giải Sách bài tập Toán lớp 7 Bài 5: Đường trung trực của một đoạn thẳng

Bài 1 trang 55 SBT Toán 7 Tập 2: Cho ba tam giác cân MAB, NAB, PAB có chung đáy AB. Chứng minh ba điểm M, N, P thẳng hàng.

Lời giải

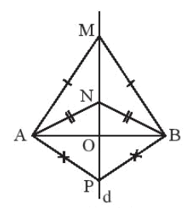
Vì tam giác cân MAB có đáy AB nên cân tại M, do đó MA = MB.

Suy ra M thuộc đường trung trực của AB     (1)

Tương tự với $∆$NAB và $∆$PAB có chung đáy AB, ta có: NA = NB, PA = PB.

Suy ra N, P cũng thuộc đường trung trực của AB   (2)

Từ (1) và (2) ta có các điểm M, N, P cùng thuộc trung trực của AB.

Do đó M, N, P thẳng hàng.

Vậy ba điểm M, N, P thẳng hàng.

Bài 2 trang 55 SBT Toán 7 Tập 2: Cho góc xOy bằng 45° và điểm M nằm trong góc xOy. Vẽ điểm N sao cho Ox là trung trực của MN, vẽ điểm P sao cho Oy là trung trực của MP.

a) Chứng minh ON = OP.

b) Tính số đo góc NOP.

Lời giải

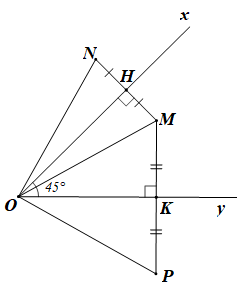
a) Ta có Ox là trung trực của MN (giả thiết).

Suy ra OM = ON (tính chất đường trung trực của một đoạn thẳng).

Vì Oy là trung trực của MP (giả thiết).

Nên OM = OP (tính chất đường trung trực của một đoạn thẳng).

Suy ra ON = OP (= OM).

Vậy ON = OP.

b) Gọi H và K lần lượt là trung điểm của MN và MP.

Xét tam giác ONH và tam giác OMH có:

ON = OM (chứng minh câu a),

NH = MH (do H là trung điểm của MN),

OH là cạnh chung.

Do đó $∆$ONH = $∆$OMH (c.c.c).

Suy ra $\widehat{NOH}=\widehat{MOH}$ (hai góc tương ứng).

Tương tự ta có: $∆$OKM = $∆$OKP (c.c.c).

Suy ra $\widehat{KOM}=\widehat{K\text{O}P}$ (hai góc tương ứng).

Ta có $\widehat{NOP}=\widehat{NOH}+\widehat{MOH}+\widehat{K\text{O}M}+\widehat{K\text{O}P}$

Mà $\widehat{NOH}=\widehat{MOH}$, $\widehat{KOM}=\widehat{K\text{O}P}$ (chứng minh trên).

Nên $\widehat{NOP}=2\widehat{MOH}+2\widehat{K\text{O}M}=2(\widehat{MOH}+\widehat{K\text{O}M})$

Hay $\widehat{NOP}=2\widehat{K\text{OH}}=2.45°=90°$.

Vậy $\widehat{NOP}=90°.$

Bài 3 trang 55 SBT Toán 7 Tập 2: Cho hai điểm A, B là vị trí của hai nhà máy cùng ở về một phía bờ sông là đường thẳng a. Vẽ điểm C sao cho a là trung trực của AC. Lấy điểm M tùy ý trên a.

a) Chứng minh MA + MB ≥ BC.

b) Tìm vị trí của địa điểm ${\text{M}}_0$ trên bờ sông để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trậm bơm về hai nhà máy là ngắn nhất.

Lời giải

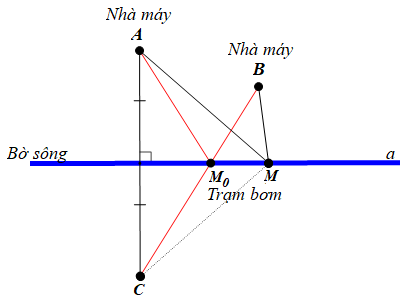
a) Vì điểm M nằm trên trung trực của AC (giả thiết).

Suy ra MA = MC

Xét tam giác BMC có MC + MB ≥ BC (bất đẳng thức tam giác).

Hay MA + MB ≥ BC

Vậy MA + MB ≥ BC.

b) Vì MA + MB ≥ BC (chứng minh câu a).

Nên MA + MB ngắn nhất khi ba điểm B, C, M thẳng hàng.

Hay điểm M₀ là giao điểm của đường thẳng BC và đường thẳng a.

Vậy điểm M₀ cần tìm là giao điểm của đường thẳng BC và đường thẳng a.

Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:

Bài 3: Tam giác cân

Bài 4: Đường vuông góc và đường xiên

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8: Tính chất ba đường cao của tam giác