Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh: a) SAMB = SAMC

Bài 1 trang 60 SBT Toán 7 Tập 2: Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh:

a) S_AMB = S_AMC;

b) S_ABG = 2S_BMG;

c) S_GAB = S_GBC = S_GAC.

Trả lời

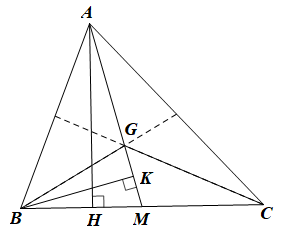
a) Vẽ đường cao AH của tam giác ABC.

Vì AM là trung tuyến của tam giác ABC nên BM = CM.

Ta có : ${\text{S}}_{\text{AMB}}=\frac{1}{2}.\text{AH.BM}$ và ${\text{S}}_{\text{AMC}}=\frac{1}{2}.\text{AH.MC}$

Hai tam giác AMB và AMC có cùng đường cao AH và có cạnh đáy bằng nhau.

Suy ra S_AMB = S_AMC.

Vậy S_AMB = S_AMC.

b) Vẽ đường cao BK của tam giác ABM.

Ta có: ${\text{S}}_{\text{ABG}}=\frac{1}{2}.\text{BK.AG}$ và ${\text{S}}_{\text{BMG}}=\frac{1}{2}.\text{BK.GM}$

Mà G là trọng tâm của tam giác ABC nên $\frac{GM}{GA}=\frac{1}{2}$ hay AG = 2GM.

Hai tam giác ABG và BMG có cùng đường cao BK và có cạnh đáy AG = 2GM.

Suy ra S_ABG = 2S_BMG.

Vậy S_ABG = 2S_BMG.

c) Ta có: S_AMB = S_AMC (chứng minh câu a) và S_AMB + S_AMC = S_ABC

Nên ${\text{S}}_{\text{AMB}}={\text{S}}_{\text{AMC}}=\frac{1}{2}{\text{S}}_{\text{ACB}}$

Vì G là trọng tâm của tam giác ABC nên AG = $\frac{1}{2}$AM.

Lại có: ${\text{S}}_{\text{GAB}}=\frac{1}{2}.\text{BK.AG}$ và ${\text{S}}_{\text{AMB}}=\frac{1}{2}.\text{BK.AM}$

Suy ra $S_{GAB}=\frac{1}{2}.\text{BK.}\frac{2}{3}\text{AM}=\frac{2}{3}{S}_{ABM}$$=\frac{2}{3}.\frac{1}{2}{S}_{ABC}=\frac{1}{3}{S}_{ABC}$

Chứng minh tương tự ta có $S_{GAC}=\frac{2}{3}{S}_{ACM}=\frac{1}{3}{S}_{ABC}$

Ta có  S_GAB + S_GAC + S_GBC = S_ABC

Mà $S_{ABG}=\frac{1}{3}{S}_{ABC}$; $S_{ACG}=\frac{1}{3}{S}_{ABC}$

Suy ra $S_{BCG}=\frac{1}{3}{S}_{ABC}$

Do đó $S_{GAB}=S_{GBC}=S_{GAC}\left(=\frac{1}{3}{S}_{ABC}\right)$

Vậy S_GAB = S_GBC = S_GAC.

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài tập cuối chương 8