Giải SBT Toán 7 (Cánh diều) Bài 3: Hai đường thẳng song song

Giải Sách bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song

Giải SBT Toán 7 trang 110 Tập 1

Bài 16 trang 110 SBT Toán 7 Tập 1: Quan sát Hình 28, biết a // b, ${\widehat{M}}_3=50°.$

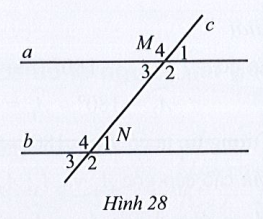
a) Nêu những cặp góc so le trong, những cặp góc đồng vị.

b) Tìm số đo mỗi góc còn lại của đỉnh M và N.

Lời giải:

a) Những cặp góc so le trong là: ${\widehat{M}}_2$ và ${\widehat{N}}_4,$ ${\widehat{M}}_3$ và ${\widehat{N}}_1.$

Những cặp góc đồng vị là: ${\widehat{M}}_1$ và ${\widehat{N}}_1,$ ${\widehat{M}}_2$ và ${\widehat{N}}_2,$${\widehat{M}}_3$ và ${\widehat{N}}_3,$${\widehat{M}}_4$ và ${\widehat{N}}_4$

b)

– Tại đỉnh M:

•  Vì ${\widehat{M}}_1$ và ${\widehat{M}}_3$ là hai góc đối đỉnh nên:

${\widehat{M}}_1={\widehat{M}}_3=50°.$

• Vì ${\widehat{M}}_2$ và ${\widehat{M}}_3$ là hai góc kề bù nên:

${\widehat{M}}_2+{\widehat{M}}_3=180°$

Suy ra ${\widehat{M}}_2=180°-{\widehat{M}}_3=180°-50°=130°.$

Vì ${\widehat{M}}_2$ và ${\widehat{M}}_4$ là hai góc đối đỉnh nên:

${\widehat{M}}_2={\widehat{M}}_4=130°.$

– Tại đỉnh N:

Vì a // b nên

• ${\widehat{N}}_1={\widehat{M}}_3=50°$ (hai góc so le trong).

• ${\widehat{N}}_2={\widehat{M}}_2=130°$ (hai góc đồng vị).

• ${\widehat{N}}_3={\widehat{M}}_3=50°$ (hai góc đồng vị).

• ${\widehat{N}}_4={\widehat{M}}_2=130°$ (hai góc so le trong).

Vậy ${\widehat{M}}_1=50°,{\widehat{M}}_2={\widehat{M}}_4=130°;$${\widehat{N}}_1={\widehat{N}}_3=50°,{\widehat{N}}_2={\widehat{N}}_4=130°.$

Bài 17 trang 110 SBT Toán 7 Tập 1: Quan sát Hình 29, biết a // b, $3{\widehat{A}}_1=2{\widehat{A}}_2.$ Tìm số đo mỗi góc của đỉnh A và B.

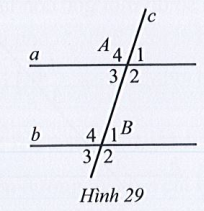
Lời giải:

– Tại đỉnh A:

• Ta có ${\widehat{A}}_1+{\widehat{A}}_2=180°$  (hai góc kề bù).

Mà $3{\widehat{A}}_1=2{\widehat{A}}_2$ hay ${\widehat{A}}_1=\frac{3}{2}{\widehat{A}}_2$

Nên $\frac{2}{3}{\widehat{A}}_2+{\widehat{A}}_2=180°$

Do đó $\frac{5}{3}{\widehat{A}}_2=180°$

Suy ra ${\widehat{A}}_2=180°:\frac{5}{3}=108°.$

Khi đó ${\widehat{A}}_1=\frac{2}{3}{\widehat{A}}_2=\frac{2}{3}.108°=72°.$

• ${\widehat{A}}_3={\widehat{A}}_1=72°$ (hai góc đối đỉnh).

• ${\widehat{A}}_4={\widehat{A}}_2=108°$ (hai góc đối đỉnh).

– Tại đỉnh B: Vì a // b nên ta có:

• ${\widehat{B}}_1={\widehat{A}}_3=72°$ (hai góc so le trong).

• ${\widehat{B}}_2={\widehat{A}}_2=108°$ (hai góc đồng vị).

• ${\widehat{B}}_3={\widehat{A}}_3=72°$ (hai góc đồng vị).

• ${\widehat{B}}_4={\widehat{A}}_2=108°$ (hai góc so le trong).

Vậy ${\widehat{A}}_1={\widehat{A}}_3={\widehat{B}}_1={\widehat{B}}_3=72°,$${\widehat{A}}_2={\widehat{A}}_4={\widehat{B}}_2={\widehat{B}}_4=108°.$

Bài 18 trang 110 SBT Toán 7 Tập 1: Tìm số đo mỗi góc B₁, B₂, B₃, B₄ trong Hình 30, biết m // n.

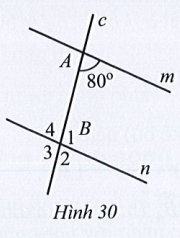
Lời giải:

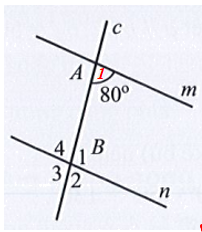
Giả sử ${\widehat{A}}_1=80°$ như hình vẽ.

Vì m // n nên ta có:

• ${\widehat{B}}_4={\widehat{A}}_1=80°$ (hai góc so le trong);

• ${\widehat{B}}_2={\widehat{A}}_1=80°$(hai góc đồng vị).

• ${\widehat{B}}_1+{\widehat{A}}_1=180°$ (hai góc trong cùng phía)

Suy ra ${\widehat{B}}_1=180°-{\widehat{A}}_1=180°-80°=100°.$

Do đó ${\widehat{B}}_3={\widehat{B}}_1=100°$ (hai góc đối đỉnh).

Vậy ${\widehat{B}}_1={\widehat{B}}_3=100°,{\widehat{B}}_2={\widehat{B}}_4=80°.$

Bài 19 trang 110 SBT Toán 7 Tập 1: Quan sát Hình 31, biết ${\widehat{P}}_3={\widehat{Q}}_1=75°,$${\widehat{M}}_3=100°.$ Tìm số đo mỗi góc còn lại của đỉnh M và N.

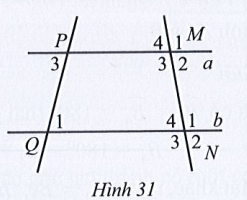
Lời giải:

+) Ta có: ${\widehat{M}}_1={\widehat{M}}_3=100°$(hai góc đối đỉnh).

Vì ${\widehat{M}}_1$ và ${\widehat{M}}_2$ là hai góc kề bù nên ta có:

${\widehat{M}}_1+{\widehat{M}}_2=180°$

Suy ra ${\widehat{M}}_2=180°-{\widehat{M}}_1$$=180°-100°=80°.$

Do đó ${\widehat{M}}_4={\widehat{M}}_2=80°$(hai góc đối đỉnh).

+) Ta có ${\widehat{P}}_3={\widehat{Q}}_1=75°$ mà hai góc này ở vị trí so le trong

Nên PM // QN.

Do đó:

• ${\widehat{N}}_1={\widehat{M}}_3=100°$ (hai góc so le trong).

• ${\widehat{N}}_2={\widehat{M}}_2=80°$ (hai góc đồng vị).

• ${\widehat{N}}_3={\widehat{M}}_3=100°$ (hai góc đồng vị).

• ${\widehat{N}}_4={\widehat{M}}_2=80°$ (hai góc so le trong).

Vậy ${\widehat{M}}_3={\widehat{N}}_1={\widehat{N}}_3=100°$ và  ${\widehat{M}}_2={\widehat{M}}_4={\widehat{N}}_2={\widehat{N}}_4=80°.$

Bài 20 trang 110 SBT Toán 7 Tập 1: Tìm số đo x, y trong Hình 32.

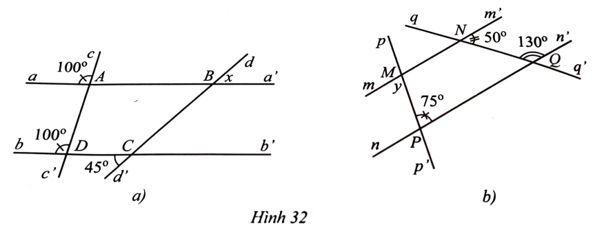
Lời giải:

a) Ta có $\widehat{\text{aAc}}=\widehat{bDc}$ (cùng bằng 100°).

Mà hai góc này ở vị trí đồng vị.

Do đó aa' // bb'.

Suy ra $\widehat{dB{a}^{\text{'}}}=\widehat{bC{d}^{\text{'}}}=45°$ (hai góc do le ngoài).

Vậy x = 45°.

b) Vì $\widehat{qQn}$ và $\widehat{qQ{n}^{\text{'}}}$ là hai góc kề bù nên ta có:

$\widehat{qQn}+\widehat{qQ{n}^{\text{'}}}=180°$

Suy ra $\widehat{qQn}=180°-\widehat{qQ{n}^{\text{'}}}$$=180°-130°=50°.$

Do đó $\widehat{m^{\text{'}}N{q}^{\text{'}}}=\widehat{qQn}$ (cùng bằng 50°).

Mà hai góc này ở vị trí so le trong nên mm' // nn'.

Suy ra $\widehat{mM{p}^{\text{'}}}=\widehat{pP{n}^{\text{'}}}=75°.$

Vậy y = 75°.

Giải SBT Toán 7 trang 111 Tập 1

Bài 21 trang 111 SBT Toán 7 Tập 1: Tìm số đo góc BCD trong Hình 33.

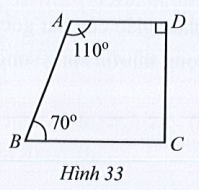
Lời giải:

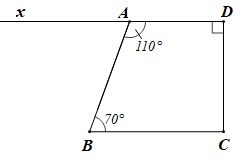
Vẽ tia Ax là tia đối của tia AD.

Khi đó $\widehat{xAB}$ và $\widehat{BAD}$ là hai góc kề bù nên ta có:

$\widehat{xAB}+\widehat{BAD}=180°$

Suy ra $\widehat{xAB}=180°-\widehat{BAD}$$=180°-110°=70°.$

Do đó $\widehat{xAB}=\widehat{ABC}$ (cùng bằng 70°).

Mà hai góc này ở vị trí so le trong nên Dx // Cy.

Suy ra $\widehat{BCD}+\widehat{ADC}=180°$ (hai góc trong cùng phía)

Do đó $\widehat{BCD}=180°-\widehat{ADC}$$=180°-90°=90°.$

Vậy $\widehat{BCD}=90°.$

Bài 22 trang 111 SBT Toán 7 Tập 1: Quan sát Hình 34, biết d₁ // d₂ và góc tù tạo bởi đường thẳng a và đường thẳng d₁ bằng 150°. Tính góc nhọn tạo bởi đường thẳng a và đường thẳng d₂.

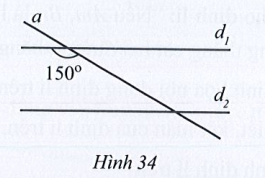
Lời giải:

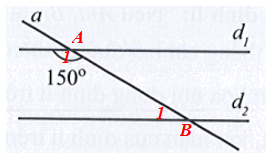
Giả sử ${\widehat{A}}_1=150°$ là góc tù được tạo bởi đường thẳng a và đường thẳng d₁;

${\widehat{B}}_1$ là góc nhọn được tạo bởi đường thẳng a và đường thẳng d₂.

Vì d₁ // d₂ nên ${\widehat{A}}_1+{\widehat{B}}_1=180°$ (hai góc trong cùng phía).

Do đó ${\widehat{B}}_1=180°-{\widehat{A}}_1$$=180°-150°=30°.$

Vậy góc nhọn được tạo bởi đường thẳng a và đường thẳng d₂ bằng 30°.

Bài 23 trang 111 SBT Toán 7 Tập 1: Quan sát Hình 35, biết xx' //  yy' // zz'. Chứng tỏ rằng $\widehat{ACB}=\widehat{CA{x}^{\text{'}}}+\widehat{CB{y}^{\text{'}}}.$

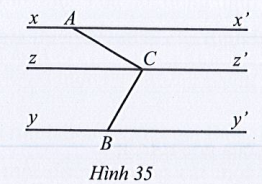
Lời giải:

Vì xx' //  zz' nên $\widehat{CA{x}^{\text{'}}}=\widehat{ACz}$ (hai góc so le trong).

Vì yy' // zz' nên $\widehat{zCB}=\widehat{CB{y}^{\text{'}}}$ (hai góc so le trong).

Mặt khác: $\widehat{ACz}$ và $\widehat{zCB}$ là hai góc kề nhau

Nên $\widehat{ACz}+\widehat{zCB}=\widehat{ACB}$

Do đó $\widehat{ACB}=\widehat{ACz}+\widehat{zCB}=\widehat{CA{x}^{\text{'}}}+\widehat{zCB}.$

Vậy $\widehat{ACB}=\widehat{CA{x}^{\text{'}}}+\widehat{CB{y}^{\text{'}}}.$

Bài 24* trang 111 SBT Toán 7 Tập 1: Bạn Khôi vẽ hai đường thẳng a và b cắt nhau tại một điểm ở ngoài phạm vi tờ giấy (Hình 36). Em hãy giúp bạn Khôi nêu cách đo góc nhọn tạo bởi hai đường thẳng a và b đã vẽ.

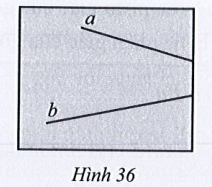
Lời giải:

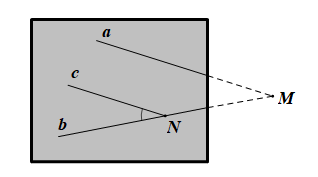
Giả sử đường thẳng a và đường thẳng b cắt nhau tại M nằm ngoài tờ giấy.

Khi đó góc nhọn tạo bởi hai đường thẳng a và b là $\widehat{aMb}.$

Trên đường thẳng b ta lấy điểm N, kẻ Nc // a sao cho $\widehat{bNc}$ là góc nhọn (hình vẽ).

Vì Nc // a nên $\widehat{bNc}=\widehat{aMb}$ (hai góc đồng vị).

Do đó ta đo góc bNc sẽ suy ra số đo của góc $\widehat{aMb}$ được tạo bởi hai đường thẳng a và b.

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 1: Góc ở vị trí đặc biệt

Bài 2: Tia phân giác của một góc

Bài 4: Định lí

Bài tập cuối chương 4

Bài 1: Thu thập, phân loại và biểu diễn dữ liệu