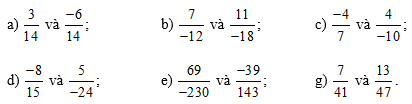Giải SBT Toán 6 (Cánh diều) Bài 2: So sánh các phân số. Hỗn số dương

Sách bài tập Toán 6 Bài 2: So sánh các phân số. Hỗn số dương

Bài 15 trang 34 sách bài tập Toán lớp 6 Tập 2: So sánh các phân số sau:

Lời giải:

a) $\frac{3}{14}$ và $\frac{-6}{14}$

Vì 3 > – 6 nên $\frac{3}{14}>\frac{-6}{14}$.

Vậy $\frac{3}{14}>\frac{-6}{14}$.

b) $\frac{7}{-12}$ và $\frac{11}{-18}$

Ta có $\frac{7}{-12}=\frac{7.\left(-3\right)}{\left(-12\right).\left(-3\right)}=\frac{-21}{36}$;

$\frac{11}{-18}=\frac{11.\left(-2\right)}{\left(-18\right).\left(-2\right)}=\frac{-22}{36}$.

Vì – 21 > – 22 nên $\frac{-21}{36}>\frac{-22}{36}$ hay $\frac{7}{-12}>\frac{11}{-18}$.

Vậy $\frac{7}{-12}>\frac{11}{-18}$.

c) $\frac{-4}{7}$ và $\frac{4}{-10}$

Ta có: $\frac{4}{-10}=\frac{-4}{10}$

Vì 7 < 10 nên $\frac{-4}{7}<\frac{-4}{10}$ hay $\frac{-4}{7}<\frac{4}{-10}$.

Vậy $\frac{-4}{7}<\frac{4}{-10}$.

d) $\frac{-8}{15}$ và $\frac{5}{-24}$

Ta có: $\frac{-8}{15}=\frac{\left(-8\right).8}{15.8}=\frac{-64}{120}$;

$\frac{5}{-24}=\frac{5.\left(-5\right)}{\left(-24\right).\left(-5\right)}=\frac{-25}{120}$.

Vì – 64 < – 25 nên $\frac{-64}{120}<\frac{-25}{120}$ hay $\frac{-8}{15}<\frac{5}{-24}$.

Vậy $\frac{-8}{15}<\frac{5}{-24}$.

e) $\frac{69}{-230}$ và $\frac{-39}{143}$;

Ta có: $\frac{69}{-230}=\frac{69:\left(-23\right)}{\left(-230\right):\left(-23\right)}=\frac{-3}{10}$;

$\frac{-39}{143}=\frac{\left(-39\right):13}{143:13}=\frac{-3}{11}$.

Vì 10 < 11 nên $\frac{-3}{10}<\frac{-3}{11}$ hay $\frac{69}{-230}<\frac{-39}{143}$.

Vậy $\frac{69}{-230}<\frac{-39}{143}$.

g) $\frac{7}{41}$ và $\frac{13}{47}$

Ta có: $1-\frac{7}{41}=\frac{41}{41}-\frac{7}{41}=\frac{34}{41}$;

$1-\frac{13}{47}=\frac{47}{47}-\frac{13}{47}=\frac{34}{47}$.

Vì 41 < 47 nên $\frac{34}{41}>\frac{34}{47}$ hay $1-\frac{7}{41}>1-\frac{13}{47}$

Do đó $\frac{7}{41}<\frac{13}{41}$.

Vậy $\frac{7}{41}<\frac{13}{41}$.

Bài 16 trang 34 sách bài tập Toán lớp 6 Tập 2:

1) Viết các phân số sau theo thứ tự tăng dần:

a) $\frac{-7}{9};\frac{3}{2};\frac{-7}{5};0;\frac{-4}{-3}$;

b) $\frac{-2}{5};\frac{5}{-6};\frac{7}{12};\frac{5}{-24};\frac{17}{30};\frac{-11}{20}$.

2) Viết các phân số sau theo thứ tự giảm dần:

a) $\frac{5}{14};\frac{3}{-40};\frac{-13}{-140};\frac{8}{-35}$;

b) $\frac{3}{400};\frac{-6}{217};\frac{-7}{-284};\frac{112}{-305}$.

Lời giải:

1) Viết các phân số theo thứ tự tăng dần:

a) $\frac{-7}{9};\frac{3}{2};\frac{-7}{5};0;\frac{-4}{-3}$

Ta có $\frac{-4}{-3}=\frac{4}{3}$.

Ta chia các phân số trên thành 3 nhóm:

+ Nhóm 1: gồm các phân số âm $\frac{-7}{9}$ và $\frac{-7}{5}$;

+ Nhóm 2: gồm số 0;

+ Nhóm 3: gồm các phân số dương $\frac{3}{2}$ và $\frac{4}{3}$.

• So sánh nhóm 1: $\frac{-7}{9}$ và $\frac{-7}{5}$

Vì 9 > 5 nên $\frac{-7}{9}>\frac{-7}{5}$.

• So sánh nhóm 3: $\frac{3}{2}$ và $\frac{4}{3}$

Ta có $\frac{3}{2}=\frac{3.3}{2.3}=\frac{9}{6}$ và $\frac{4}{3}=\frac{4.2}{3.2}=\frac{8}{6}$.

Vì 9 > 8 nên $\frac{9}{6}>\frac{8}{6}$ hay $\frac{3}{2}>\frac{4}{3}$.

• Ta đã biết số 0 luôn lớn hơn phân số âm và nhỏ hơn phân số dương.

Do đó ta có: $\frac{-7}{5}<\frac{-7}{9}<0<\frac{4}{3}<\frac{3}{2}$ hay $\frac{-7}{5}<\frac{-7}{9}<0<\frac{-4}{-3}<\frac{3}{2}$.

Vậy viết các số theo thứ tự tăng dần ta có $\frac{-7}{5};\frac{-7}{9};0;\frac{-4}{-3};\frac{3}{2}$.

b) $\frac{-2}{5};\frac{5}{-6};\frac{7}{12};\frac{5}{-24};\frac{17}{30};\frac{-11}{20}$

Ta chia các phân số trên thành 2 nhóm:

+ Nhóm 1: gồm các phân số âm $\frac{-2}{5};\frac{5}{-6};\frac{5}{-24}$ và $\frac{-11}{20}$;

+ Nhóm 2: gồm các phân số dương $\frac{7}{12}$ và $\frac{17}{30}$.

• So sánh nhóm 1: $\frac{-2}{5};\frac{-5}{6};\frac{-5}{24}$ và $\frac{-11}{20}$

Ta có $\frac{-2}{5}=\frac{\left(-2\right).24}{5.24}=\frac{-48}{120}$;

$\frac{5}{-6}=\frac{5.\left(-20\right)}{\left(-6\right).\left(-20\right)}=\frac{-100}{120}$;

$\frac{5}{-24}=\frac{5.\left(-5\right)}{\left(-24\right).\left(-5\right)}=\frac{-25}{120}$;

$\frac{-11}{20}=\frac{\left(-11\right).6}{20.6}=\frac{-66}{120}$.

Vì – 100 < – 66 < – 48 < – 25

Nên $\frac{-100}{120}<\frac{-66}{120}<\frac{-48}{120}<\frac{-25}{120}$

Do đó $\frac{5}{-6}<\frac{-11}{20}<\frac{-2}{5}<\frac{5}{-24}$.

• So sánh nhóm 2: $\frac{7}{12}$ và $\frac{17}{30}$

Ta có $\frac{7}{12}=\frac{7.5}{12.5}=\frac{35}{60}$ và $\frac{17}{30}=\frac{17.2}{30.2}=\frac{34}{60}$.

Vì 34 < 35 nên $\frac{34}{60}<\frac{35}{60}$ do đó $\frac{17}{30}<\frac{7}{12}$.

• Ta đã biết phân số âm luôn nhỏ hơn phân số dương nên ta có:

$\frac{5}{-6}<\frac{-11}{20}<\frac{-2}{5}<\frac{5}{-24}<\frac{17}{30}<\frac{7}{12}$.

Vậy viết các số theo thứ tự tăng dần ta được $\frac{5}{-6};\frac{-11}{20};\frac{-2}{5};\frac{5}{-24};\frac{17}{30};\frac{7}{12}$.

2) Viết các phân số theo thứ tự giảm dần:

a) $\frac{5}{14};\frac{3}{-40};\frac{-13}{-140};\frac{8}{-35}$

Ta có $\frac{-13}{-140}=\frac{13}{140}$.

Ta chia các phân số trên thành 2 nhóm:

+ Nhóm 1: gồm các phân số âm $\frac{3}{-40}$ và $\frac{8}{-35}$;

+ Nhóm 2: gồm các phân số dương $\frac{5}{14}$ và $\frac{13}{140}$.

• So sánh nhóm 1: $\frac{3}{-40}$ và $\frac{8}{-35}$

Ta có $\frac{3}{-40}=\frac{3.\left(-8\right)}{\left(-40\right).\left(-8\right)}=\frac{-24}{320}$;

$\frac{8}{-35}=\frac{8.\left(-3\right)}{\left(-35\right).\left(-3\right)}=\frac{-24}{105}$

Vì 320 > 105 nên $\frac{-24}{320}>\frac{-24}{105}$

Do đó $\frac{3}{-40}>\frac{8}{-35}$.

• So sánh nhóm 2: $\frac{5}{14}$ và $\frac{13}{140}$

Ta có $\frac{5}{14}=\frac{5.10}{14.10}=\frac{50}{140}$.

Vì 50 > 13 nên $\frac{50}{140}>\frac{13}{140}$

Do đó $\frac{50}{140}>\frac{-13}{-140}$

• Ta đã biết phân số dương luôn lớn hơn phân số âm nên ta có:

$\frac{5}{14}>\frac{-13}{-140}>\frac{3}{-40}>\frac{8}{-35}.$

Vậy các phân số theo thứ tự giảm dần ta được $\frac{5}{14};\frac{-13}{-140};\frac{3}{-40};\frac{8}{-35}.$

b) $\frac{3}{400};\frac{-6}{217};\frac{-7}{-284};\frac{112}{-305}$

Ta có $\frac{-7}{-284}=\frac{7}{284}$.

Ta chia các phân số trên thành 2 nhóm:

+ Nhóm 1: gồm các phân số âm $\frac{-6}{217}$ và $\frac{112}{-305}$;

+ Nhóm 2: gồm các phân số dương $\frac{3}{400}$ và $\frac{7}{284}$.

• So sánh nhóm 1: $\frac{-6}{217}$ và $\frac{112}{-305}$

Ta có $\frac{-6}{217}=\frac{\left(-6\right).56}{217.56}=\frac{-336}{12152}$;

$\frac{112}{-305}=\frac{112.\left(-3\right)}{\left(-305\right).\left(-3\right)}=\frac{-336}{915}$.

Vì 12 152 > 915 nên $\frac{-336}{12152}>\frac{-336}{915}$.

Do đó $\frac{-6}{217}>\frac{112}{-305}$.

• So sánh nhóm 2: $\frac{3}{400}$ và $\frac{7}{284}$

Ta có $\frac{3}{400}=\frac{3.7}{400.7}=\frac{21}{2800}$;

$\frac{7}{284}=\frac{7.3}{7.3}=\frac{21}{852}$.

Vì 852 < 2 800 nên $\frac{21}{852}>\frac{21}{2800}$.

Do đó $\frac{7}{284}>\frac{3}{400}$ hay $\frac{-7}{-284}>\frac{3}{400}$.

• Ta đã biết phân số dương luôn lớn hơn phân số âm nên ta có:

$\frac{-7}{-284}>\frac{3}{400}>\frac{-6}{217}>\frac{112}{-305}$.

Vậy các phân số theo thứ tự giàm dần ta được $\frac{-7}{-284};\frac{3}{400};\frac{-6}{217};\frac{112}{-305}$.

Bài 17 trang 34 sách bài tập Toán lớp 6 Tập 2:Tìm số nguyên thích hợp điền vào chỗ chấm (…):

a) $\frac{-12}{19}<\frac{\dots }{19}<\frac{\dots }{19}<\frac{\dots }{19}<\frac{-8}{19}$;

b) $\frac{-1}{2}<\frac{\cdots }{24}<\frac{\cdots }{12}<\frac{\cdots }{8}<\frac{-1}{3}$.

Lời giải:

a) $\frac{-12}{19}<\frac{\dots }{19}<\frac{\dots }{19}<\frac{\dots }{19}<\frac{-8}{19}$

Đặt $\frac{-12}{19}<\frac{x}{19}<\frac{y}{19}<\frac{z}{19}<\frac{-8}{19}$ (với x, y, z ∈ ℤ).

Ta thấy các phân số có cùng một mẫu số dương, phân số nào có tử số nhỏ hơn thì nhỏ hơn.

Do đó ta có – 12 < x < y < z < – 8.

Mà x, y, z ∈ ℤ và – 12 < – 11 < – 10 < – 9 < – 8.

Suy ra x = – 11, y = – 10, z = – 9.

Vậy ta điền như sau: $\frac{-12}{19}<\frac{-11}{19}<\frac{-10}{19}<\frac{-9}{19}<\frac{-8}{19}$

b) $\frac{-1}{2}<\frac{\cdots }{24}<\frac{\cdots }{12}<\frac{\cdots }{8}<\frac{-1}{3}$

Đặt $\frac{-1}{2}<\frac{x}{24}<\frac{y}{12}<\frac{z}{8}<\frac{-1}{3}$ (với x, y, z ∈ ℤ).

Suy ra $\frac{-12}{24}<\frac{x}{24}<\frac{2y}{24}<\frac{3z}{24}<\frac{-8}{24}$

Do đó – 12 < x < 2y < 3z < – 8.

Mà x, y, z ∈ ℤ và – 12 < – 11 < – 10 < – 9 < – 8.

Nên ta có: x = –11; 2y = –10; 3z = –9

Hay x = –11; y = –5 và z = –3.

Vậy ta điền như sau: $\frac{-1}{2}<\frac{-11}{24}<\frac{-5}{12}<\frac{-3}{8}<\frac{-1}{3}$.

Bài 18 trang 34 sách bài tập Toán lớp 6 Tập 2: Viết các hỗn số thích hợp vào chỗ chấm (...):

a) 4 m 7 dm = … m;

b) 3 kg 315 g = … kg;

c) 5 giờ 45 phút = … giờ;

d) 21 m² 8 dm² = … m².

Lời giải:

a) 4 m 7 dm = … m

Đổi 4 m 7 dm = $4+\frac{7}{10}$ m = $4\frac{7}{10}$ m.

Vậy ta điền hỗn số $4\frac{7}{10}$.

b) 3 kg 315 g = … kg

Đổi 3 kg 315 g = $3+\frac{315}{1000}$ kg = $3+\frac{63}{500}$ kg = $3\frac{63}{500}$ kg.

Vậy ta điền hỗn số $3\frac{63}{500}$.

c) 5 giờ 45 phút = … giờ

Đổi 5 giờ 45 phút = $5+\frac{45}{60}$ giờ = $5+\frac{3}{4}$ giờ = $5\frac{3}{4}$ giờ.

Vậy ta điền hỗn số $5\frac{3}{4}$.

d) 21 m² 8 dm² = … m²

Đổi 21 m² 8 dm² = $21+\frac{8}{100}$ m² = $21+\frac{2}{25}$ m² = $21\frac{2}{25}$ m².

Vậy ta điền hỗn số $21\frac{2}{25}$.

Bài 19 trang 34 sách bài tập Toán lớp 6 Tập 2: Lúc 7 giờ 15 phút, một xe máy đi từ A đến B. Biết xe máy đi từ A đến B hết 1 giờ 20 phút. Xe máy đến B lúc mấy giờ? Viết kết quả dưới dạng hỗn số với đơn vị giờ.

Lời giải:

Xe máy đến B lúc:

7 giờ 15 phút + 1 giờ 20 phút = 8 giờ 35 phút.

Đổi 8 giờ 35 phút = $8\frac{35}{60}$giờ = $8\frac{7}{12}$giờ.

Vậy xe máy đến B lúc $8\frac{7}{12}$giờ.

Bài 20 trang 34 sách bài tập Toán lớp 6 Tập 2: Các bạn Đức, Hoà, Bình tham gia một cuộc thi chạy 100 m. Bạn Đức chạy mất $\frac{3}{10}$ phút, bạn Hoà chạy mất $\frac{7}{15}$ phút, bạn Bình chạy mất $\frac{7}{30}$ phút. Bạn nào chạy nhanh nhất?

Lời giải:

Ta có $\frac{3}{10}=\frac{9}{30};\frac{7}{15}=\frac{14}{30}$

Vì 7 < 9 < 14 nên $\frac{7}{30}<\frac{9}{30}<\frac{14}{30}$ hay $\frac{7}{30}<\frac{3}{10}<\frac{7}{15}$.

Do đó Bình chạy nhanh nhất vì bạn ấy chạy hết 100 m trong thời gian ngắn nhất.

Vậy bạn Bình chạy nhanh nhất.

Bài 21 trang 35 sách bài tập Toán lớp 6 Tập 2: Hai người cùng đi quãng đường như nhau từ nhà đến siêu thị. Người thứ nhất đi hết 32 phút, người thứ hai đi hết 48 phút. Biết rằng vận tốc của mỗi người không đổi.

a) So sánh quãng đường người thứ nhất đi trong 20 phút với quãng đường người thứ hai đi trong 25 phút.

b) Người thứ hai phải đi trong bao lâu để được quãng đường bằng người thứ nhất đi trong 24 phút?

Lời giải:

a)• Người thứ nhất đi hết quãng đường từ nhà đến siêu thị trong 32 phút nên trong 1 phút người thứ nhất đi được$\frac{1}{32}$ quãng đường.

Do đó trong 20 phút người thứ nhất đi được$20.\frac{1}{32}=\frac{5}{8}$ quãng đường.

• Người thứ hai đi hết quãng đường từ nhà đến siêu thị trong 48 phút nên trong 1 phút người thứ hai đi được $\frac{1}{48}$quãng đường.

Do đó trong 25 phút người thứ hai đi được $\frac{25}{48}$quãng đường.

•Để so sánh quãng đường hai người đã đi ta quy về so sánh hai phân số $\frac{5}{8}$và $\frac{25}{48}$.

Ta có: $\frac{5}{8}=\frac{5.6}{8.6}=\frac{30}{48}$.

Mà 25 < 30 nên $\frac{25}{48}<\frac{30}{48}$ hay $\frac{25}{48}<\frac{5}{8}$.

Vậy quãng đường người thứ nhất đi trong 20 phút dài hơn quãng đường người thứ hai đitrong 25 phút.

b) Trong 24 phútngười thứ nhất đi được $\frac{24}{32}=\frac{3}{4}$ quãng đường.

Khi đó thời gian để người thứ hai đi được $\frac{3}{4}$ quãng đường đó là:

$\frac{3}{4}:\frac{1}{48}=\frac{3}{4}.\frac{48}{1}=36$ (phút).

Vậy người thứ hai phải đi trong 36 phút để được quãng đường bằng người thứ nhất đi trong 24 phút.

Bài 22 trang 35 sách bài tập Toán lớp 6 Tập 2: Theo một khảo sát lấy ý kiến bình chọn Quốc hoa được công bố vào tháng 01/2011, $\frac{62}{100}$ số người chọn hoa sen, $\frac{3}{20}$ số người chọn hoa mai, $\frac{4}{25}$ số người chọn hoa đào.

a) Hãy sắp xếp các phân số trên theo thứ tự giảm dần.

b) Loài hoa nào đã được bình chọn nhiều nhất?

Lời giải:

a) Ta có $\frac{3}{20}=\frac{15}{100};\frac{4}{25}=\frac{16}{100}$.

Mà 62 > 16 > 15 nên $\frac{62}{100}>\frac{16}{100}>\frac{15}{100}$.

Hay $\frac{62}{100}>\frac{4}{25}>\frac{3}{20}$.

Vậy sắp xếp các phân số theo thứ tự giảm dần là $\frac{62}{100};\frac{4}{25};\frac{3}{20}$.

b) Do $\frac{62}{100}$ số người chọn hoa sen mà $\frac{62}{100}$ là phân số lớn nhất nên hoa sen được bình chọn nhiều nhất.

Vậy hoa sen được bình chọn nhiều nhất.

Bài 23 trang 35 sách bài tập Toán lớp 6 Tập 2: Phân số chỉ số phần nước trong một số loại củ, quả được cho ở bảng sau:

Củ, quả nào có lượng nước chiếm tỉ lệ cao nhất? Thấp nhất?

Lời giải:

Ta có $\frac{19}{20}=\frac{95}{100};\frac{9}{10}=\frac{90}{100};\frac{22}{25}=\frac{88}{100}$

Mà 87 < 88 < 90 < 95 nên $\frac{87}{100}<\frac{88}{100}<\frac{90}{100}<\frac{95}{100}$.

Do đó $\frac{87}{100}<\frac{22}{25}<\frac{9}{10}<\frac{19}{20}$.

Vậy quả mâm xôi có tỉ lệ nước thấp nhất và củ cải trắng có tỉ lệ nước cao nhất.

Bài 24 trang 35 sách bài tập Toán lớp 6 Tập 2: Tìm phân số có mẫu bằng 7, biết rằng khi cộng tử với 16 và nhân mẫu với 5 thì giá trị của phân số đó không thay đổi.

Lời giải:

Gọi phân số cần tìm là $\frac{a}{7}$ (a ∈ ℤ).

Theo đề bài ta có: $\frac{a}{7}=\frac{a+16}{7.5}$

Hay $\frac{5a}{35}=\frac{a+16}{35}$

Suy ra 5a = a + 16

Do đó 5a – a = 16 hay 4a = 16

Nên a = 16 : 4 = 4

Thử lại ta có: $\frac{4+16}{7.5}=\frac{20}{35}=\frac{4}{7}$.

Vậy phân số cần tìm là $\frac{4}{7}$.

Bài 25 trang 35 sách bài tập Toán lớp 6 Tập 2: Theo một thống kê, trong tổng số lượng sách được người đọc yêu thích: sách kĩ năng sống chiếm $\frac{1}{4}$; sách văn học chiếm $\frac{3}{20}$; sách nuôi dạy con chiếm $\frac{3}{25}$; sách khoa học công nghệ chiếm $\frac{31}{100}$; sách kinh doanh đầu tư chiếm $\frac{17}{100}$. Sách nào được nhiều bạn đọc yêu thích nhất?

Lời giải:

Ta có $\frac{1}{4}=\frac{25}{100};\frac{3}{20}=\frac{15}{100};\frac{3}{25}=\frac{12}{100}$

Mà 12 < 15 < 17 < 25 < 31

Suy ra $\frac{12}{100}<\frac{15}{100}<\frac{17}{100}<\frac{25}{100}<\frac{31}{100}$.

Do đó $\frac{3}{25}<\frac{3}{20}<\frac{17}{100}<\frac{1}{4}<\frac{31}{100}$.

Vậy sách khoa học công nghệ được nhiều bạn đọc yêu thích nhất.

Bài 26 trang 35 sách bài tập Toán lớp 6 Tập 2: Tìm các số nguyên x, y sao cho: $\frac{1}{8}<\frac{x}{18}<\frac{y}{24}<\frac{2}{9}.$

Lời giải:

Ta có:

BCNN(8,18,24,9) = 72.

Quy đồng mẫu số các phân số ta có:

$\frac{1.9}{8.9}<\frac{x.4}{18.4}<\frac{y.3}{24.3}<\frac{2.8}{9.8}.$

Hay $\frac{9}{72}<\frac{4x}{72}<\frac{3y}{72}<\frac{16}{72}.$

Suy ra 9 < 4x < 3y < 16.

Vì x, y là các số nguyên nên 4x và 3y cũng là số nguyên.

Mà 9 < 10 < 11 < 12 < 13 < 14 < 15 < 16.

Trong các số 10, 11, 12, 13, 14, 15 thì chỉ có số 12 chia hết cho 4.

Do đó 4x = 12 nên x = 3.

Khi đó 12 < 3y < 16 mà trong các số 13, 14, 15 thì chỉ có số 15 chia hết cho 5.

Do đó 3y = 15 nên y = 5.

Vậy x = 3 và y = 5.

Xem thêm các bài giải SBT Toán 6 Cánh diều hay, chi tiết khác:

Bài ôn tập cuối chương 4

Bài 1: Phân số với tử và mẫu là số nguyên

Bài 3: Phép cộng. Phép trừ phân số

Bài 4: Phép nhân, phép chia phân số

Bài 5: Số thập phân