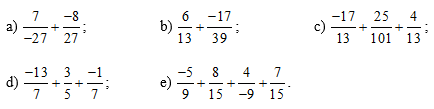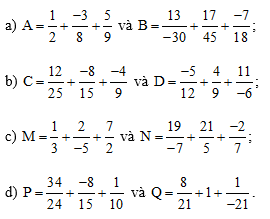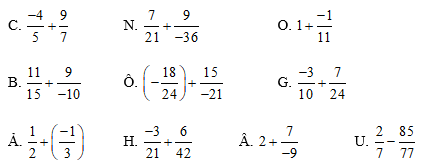Giải SBT Toán 6 (Cánh diều) Bài 3: Phép cộng, phép trừ phân số

Sách bài tập Toán 6 Bài 3: Phép cộng, phép trừ phân số

Bài 27 trang 37 sách bài tập Toán lớp 6 Tập 2: Tính các tổng sau (tính hợp lí nếu có thể):

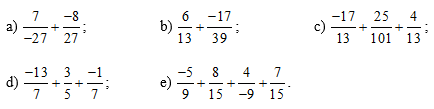
Lời giải:

a) $\frac{7}{-27}+\frac{-8}{27}=\frac{-7}{27}+\frac{-8}{27}=\frac{-15}{27}=\frac{-5}{9}$.

b) $\frac{6}{13}+\frac{-17}{39}=\frac{18}{39}+\frac{-17}{39}=\frac{1}{39}$.

c) $\frac{-17}{13}+\frac{25}{101}+\frac{4}{13}=\left(\frac{-17}{13}+\frac{4}{13}\right)+\frac{25}{101}$

$=\frac{-13}{13}+\frac{25}{101}=(-1)+\frac{25}{101}$

$=\frac{-101}{101}+\frac{25}{101}=\frac{-76}{101}$.

d) $\frac{-13}{7}+\frac{3}{5}+\frac{-1}{7}=\left(\frac{-13}{7}+\frac{-1}{7}\right)+\frac{3}{5}$

$=\frac{-14}{7}+\frac{3}{5}=(-2)+\frac{3}{5}$

$=\frac{-10}{5}+\frac{3}{5}=\frac{-7}{5}$.

e) $\frac{-5}{9}+\frac{8}{15}+\frac{4}{-9}+\frac{7}{15}$

$=\left(\frac{-5}{9}+\frac{-4}{9}\right)+\left(\frac{8}{15}+\frac{7}{15}\right)$

$=\frac{-9}{9}+\frac{15}{15}=(-1)+1=0$.

Bài 28 trang 37 sách bài tập Toán lớp 6 Tập 2: So sánh các biểu thức:

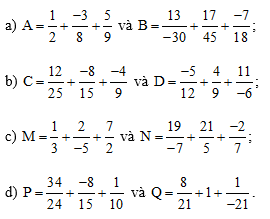
Lời giải:

a) Ta có:

$A=\frac{1}{2}+\frac{-3}{8}+\frac{5}{9}=\frac{36}{72}+\frac{-27}{72}+\frac{40}{72}=\frac{49}{72}$

và $B=\frac{13}{-30}+\frac{17}{45}+\frac{-7}{18}=\frac{-39}{90}+\frac{34}{90}+\frac{-35}{90}=\frac{-40}{90}=\frac{-4}{9}$.

Do $\frac{49}{72}>0$ và $\frac{-4}{9}<0$ nên $\frac{49}{72}>\frac{-4}{9}$.

Vậy A > B.

b) Ta có:

$C=\frac{12}{25}+\frac{-8}{15}+\frac{-4}{9}=\frac{108}{225}+\frac{-120}{225}+\frac{-100}{225}=\frac{-112}{225}$

và $D=\frac{-5}{12}+\frac{4}{9}+\frac{11}{-6}=\frac{-15}{36}+\frac{16}{36}+\frac{-66}{36}=\frac{-65}{36}$.

Vì –112 > –225 nên $\frac{-112}{225}>\frac{-225}{225}=-1$

và –65 < –36 nên $\frac{-65}{36}<\frac{-36}{36}=-1$

Suy ra $\frac{-112}{225}>-1>\frac{-65}{36}$ hay C > – 1 > D.

Vậy C > D.

c) Ta có:

$M=\frac{1}{3}+\frac{2}{-5}+\frac{7}{2}=\frac{10}{30}+\frac{-12}{30}+\frac{105}{30}=\frac{103}{30}=3\frac{13}{30}$

và $N=\frac{19}{-7}+\frac{21}{5}+\frac{-2}{7}=\left(\frac{-19}{7}+\frac{-2}{7}\right)+\frac{21}{5}$

$=\frac{-21}{7}+\frac{21}{5}=(-3)+\frac{21}{5}=\frac{-15}{5}+\frac{21}{5}=\frac{6}{5}=1\frac{1}{5}$.

Do đó $3\frac{13}{30}>3>1\frac{1}{5}$ hay M > N.

Vậy M > N.

d) Ta có:

$P=\frac{34}{24}+\frac{-8}{15}+\frac{1}{10}=\frac{17}{12}+\frac{-8}{15}+\frac{1}{10}=\frac{85}{60}+\frac{-32}{60}+\frac{6}{60}=\frac{59}{60}<1$

và $Q=\frac{8}{21}+1+\frac{1}{-21}=\left(\frac{8}{21}+\frac{-1}{21}\right)+1=\frac{7}{21}+1=\frac{1}{3}+1=1\frac{1}{3}>1$.

Do đó P < 1 < Q.

Vậy P < Q.

Bài 29 trang 37 sách bài tập Toán lớp 6 Tập 2: Không tính trực tiếp, chứng tỏ tổng của ba phân số sau: $\frac{20}{11};\frac{20}{31};\frac{20}{51}$ nhỏ hơn $\frac{7}{2}$.

Lời giải:

Đặt $A=\frac{20}{11}+\frac{20}{31}+\frac{20}{51}$.

“Làm trội” mỗi phân số để tính toán cho đơn giản:

$\frac{20}{11}<\frac{20}{10}=2;\frac{20}{31}<\frac{20}{30}=\frac{2}{3};\frac{20}{51}<\frac{20}{50}=\frac{2}{5}$.

Do đó $A<2+\frac{2}{3}+\frac{2}{5}$.

Suy ra $A<\frac{30}{15}+\frac{10}{15}+\frac{6}{15}=\frac{46}{15}=3\frac{1}{15}$.

Ta so sánh $3\frac{1}{15}$ và $\frac{7}{2}=3\frac{1}{2}$.

Do 15 > 2 nên $\frac{1}{15}<\frac{1}{2}$ do đó $3\frac{1}{15}<3\frac{1}{2}=\frac{7}{2}$

Hay $A<3\frac{1}{15}<\frac{7}{2}$.

Vậy tổng của ba phân số $\frac{20}{11};\frac{20}{31};\frac{20}{51}$ nhỏ hơn $\frac{7}{2}$

Bài 30 trang 37 sách bài tập Toán lớp 6 Tập 2: Viết tên một giáo sư đoạt giải thưởng Toán học cao quý nhất thế giới bằng cách thực hiện các yêu cầu sau: tính các tổng sau đây, rồi điền các chữ vào vị trí tương ứng với tổng vừa tính ở bảng sau:

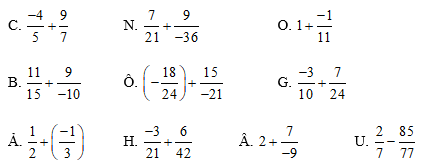
Lời giải:

Ta thực hiện các phép tính:

C. $\frac{-4}{5}+\frac{9}{7}=\frac{-28}{35}+\frac{45}{35}=\frac{17}{35}$;

N. $\frac{7}{21}+\frac{9}{-36}=\frac{1}{3}+\frac{-1}{4}=\frac{4}{12}+\frac{-3}{12}=\frac{1}{12}$;

O. $1+\frac{-1}{11}=\frac{11}{11}+\frac{-1}{11}=\frac{10}{11}$;

B. $\frac{11}{15}+\frac{9}{-10}=\frac{22}{30}+\frac{-27}{30}=\frac{-5}{30}=\frac{-1}{6}$;

Ô. $\left(-\frac{18}{24}\right)+\frac{15}{-21}=\frac{-3}{4}+\frac{-5}{7}=\frac{-21}{28}+\frac{-20}{28}=\frac{-41}{28}$;

G. $\frac{-3}{10}+\frac{7}{24}=\frac{-72}{240}+\frac{70}{240}=\frac{-2}{240}=\frac{-1}{120}$;

Ả. $\frac{1}{2}+\left(\frac{-1}{3}\right)=\frac{3}{6}+\frac{-2}{6}=\frac{1}{6}$;

H. $\frac{-3}{21}+\frac{6}{42}=\frac{-3}{21}+\frac{3}{21}=0$ ;

Â. $2+\frac{7}{-9}=\frac{18}{9}+\frac{-7}{9}=\frac{11}{9}$;

U. $\frac{2}{7}-\frac{85}{77}=\frac{22}{77}-\frac{85}{77}=\frac{-63}{77}=\frac{-9}{11}$.

Ta điền như sau:

Vậy tên giáo sư đó là “NGÔ BẢO CHÂU”.

Bài 31 trang 38 sách bài tập Toán lớp 6 Tập 2: Tìm số nguyên x, biết:

a) $\frac{-5}{7}+1+\frac{30}{-7}\le x\le \frac{-1}{6}+\frac{1}{3}+\frac{5}{6}$;

b) $\frac{-8}{13}+\frac{7}{17}+\frac{21}{13}\le x\le \frac{-9}{14}+3+\frac{5}{-14}$.

Lời giải:

a) Ta có:

$\frac{-5}{7}+1+\frac{30}{-7}\le x\le \frac{-1}{6}+\frac{1}{3}+\frac{5}{6}$

$\frac{-5}{7}+\frac{7}{7}+\frac{-30}{7}\le x\le \frac{-1}{6}+\frac{2}{6}+\frac{5}{6}$

$\frac{-28}{7}\le x\le \frac{6}{6}$

–4 ≤ x ≤ 1

Mà x ∈ ℤ, suy ra x ∈ {–4; –3; –2; –1; 0; 1}.

Vậy x ∈ {–4; –3; –2; –1; 0; 1}.

b) Ta có:

$\frac{-8}{13}+\frac{7}{17}+\frac{21}{13}\le x\le \frac{-9}{14}+3+\frac{5}{-14}$

$\left(\frac{-8}{13}+\frac{21}{13}\right)+\frac{7}{17}\le x\le \left(\frac{-9}{14}+\frac{-5}{14}\right)+3$

$\frac{13}{13}+\frac{7}{17}\le x\le \frac{-14}{14}+3$

$1+\frac{7}{17}\le x\le -1+3$

$1+\frac{7}{17}\le x\le 2$

Do đó 1 < x ≤ 2.

Mà x ∈ ℤ, suy ra $x=2$.

Vậy x = 2.

Bài 32 trang 38 sách bài tập Toán lớp 6 Tập 2: Tìm tổng các phân số đồng thời lớn hơn$\frac{-1}{2}$, nhỏ hơn $\frac{-1}{3}$ và có tử là 5.

Lời giải:

Giả sử các phân số có tử là 5 có dạng $\frac{5}{x}$ (x ∈ ℤ, x ≠ 0).

Ta có $\frac{-1}{2}<\frac{5}{x}<\frac{-1}{3}$ suy ra $\frac{5}{-10}<\frac{5}{x}<\frac{5}{-15}$

Do đó –10 > x > –15.

Mà x ∈ ℤ, suy ra x ∈ {–11; –12; –13; –14}.

Khi đó các phân số cần tìm là <$\frac{5}{-11};\frac{5}{-12};\frac{5}{-13};\frac{5}{-14}$.

Tổng các phân số trên là:

$\frac{5}{-11}+\frac{5}{-12}+\frac{5}{-13}+\frac{5}{-14}$

$=\frac{-5460}{12012}+\frac{-5005}{12012}+\frac{-4620}{12012}+\frac{-4290}{12012}$

$=\frac{-19375}{12012}$.

Vậy tổng cần tìm bằng $\frac{-19375}{12012}$.

Bài 33 trang 38 sách bài tập Toán lớp 6 Tập 2: Ba ô tô cùng chuyển long nhãn từ một kho ở Hưng Yên lên Hà Nội. Ô tô thứ nhất, thứ hai, thứ ba chuyển được lần lượt $\frac{1}{3};\frac{1}{5}$ và $\frac{2}{9}$ số long nhãn trong kho. Cả ba ô tô chuyển được bao nhiêu phần long nhãn trong kho?

Lời giải:

Cả ba ô tô chuyển được số long nhãn là:

$\frac{1}{3}+\frac{1}{5}+\frac{2}{9}=\frac{15}{45}+\frac{9}{45}+\frac{10}{45}=\frac{34}{45}$ (số long nhãn trong kho).

Vậy cả ba ô tô chuyển được$\frac{34}{45}$ số long nhãn trong kho.

Bài 34 trang 38 sách bài tập Toán lớp 6 Tập 2: Người thứ nhất đi xe đạp từ A đến B hết 5 giờ; người thứ hai đi xe máy từ B về A hết 2 giờ; người thứ hai khởi hành sau người thứ nhất 2 giờ. Hỏi sau khi người thứ hai đi được 1 giờ thì hai người đã gặp nhau chưa?

Lời giải:

Do người thứ hai khởi hành sau người thứ nhất 2 giờ nên sau khi người thứ hai đi được 1 giờ thì người thứ nhất đã đi được 3 giờ.

Người thứ nhất đi xe đạp từ A đến B hết 5 giờ nên trong 1 giờ người đi xe đạp đi được $\frac{1}{5}$ quãng đường. Do đó trong 3 giờ người đi xe đạp đi được $\frac{3}{5}$ quãng đường.

Người thứ hai đi xe máy từ B về A hết 2 giờ nên trong 1 giờ người đi xe máy đi được $\frac{1}{2}$ quãng đường.

Tổng quãng đường hai người đã đi là:

$\frac{3}{5}+\frac{1}{2}=\frac{6}{10}+\frac{5}{10}=\frac{11}{10}$ (quãng đường).

Vì $\frac{11}{10}>1$ nên tổng quãng đường hai người đi được đã lớn hơn quãng đường AB, do đó hai người đã gặp nhau.

Vậy sau khi người thứ hai đi được 1 giờ thì hai người đã gặp nhau.

Bài 35 trang 38 sách bài tập Toán lớp 6 Tập 2: Một người hỏi Py-ta-go về số học trò của ông. Ông nói: “Một nửa số học trò của tôi đang học Toán, một phần tư đang học Nhạc, một phần bảy đang ngồi suy nghĩ. Số còn lại là 3 người”. Ông có bao nhiêu học trò?

Lời giải:

Số học trò học Toán, học Nhạc và đang suy nghĩ là:

$\frac{1}{2}+\frac{1}{4}+\frac{1}{7}=\frac{14}{28}+\frac{7}{28}+\frac{4}{28}=\frac{25}{28}$ (số học trò).

Số học trò còn lại là: $1-\frac{25}{28}=\frac{3}{28}$ (số học trò).

Do đó $\frac{3}{28}$ số học trò tương ứng với 3 người.

Vậy số học trò của Py-ta-go là 28 người.

Bài 36 trang 38 sách bài tập Toán lớp 6 Tập 2: Có 5 quả cam chia đều cho 6 người. Làm thế nào để chia được mà không phải cắt bất kì quả cam nào thành 6 phần bằng nhau?

Lời giải:

Có 5 quả cam chia đều cho 6 người thì mỗi người được $\frac{5}{6}$ quả cam.

Ta có: $\frac{5}{6}=\frac{3+2}{6}=\frac{3}{6}+\frac{2}{6}=\frac{1}{2}+\frac{1}{3}$.

Do đó mỗi người được $\frac{1}{2}$ quả cam và $\frac{1}{3}$ quả cam nữa.

Vì vậy để không phải cắt bất kì một quả cam nào thành 6 phần bằng nhau ta sẽ chia như sau:

Lấy 3 quả cam, mỗi quả chia thành 2 phần bằng nhau thì có đủ 6 phần cho 6 người.

Lấy 2 quả cam còn lại, mỗi quả chia 3 thì được 6 phần bằng nhau cũng đủ chia cho 6 người.

Bài 37 trang 38 sách bài tập Toán lớp 6 Tập 2: Hoàn thành hai tháp số sau:

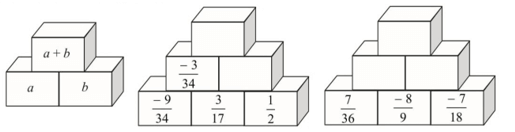
Lời giải:

Áp dụng quy tắc cho tháp số thứ nhất:

$\frac{-9}{34}+\frac{3}{17}=\frac{-9}{34}+\frac{6}{34}=\frac{-3}{34}$;

$\frac{3}{17}+\frac{1}{2}=\frac{6}{34}+\frac{17}{34}=\frac{23}{34}$;

$\frac{-3}{34}+\frac{23}{34}=\frac{20}{34}=\frac{10}{17}$;

Áp dụng quy tắc cho tháp số thứ hai:

$\frac{7}{36}+\frac{-8}{9}=\frac{7}{36}+\frac{-32}{36}=\frac{-25}{36}$;

$\frac{-8}{9}+\frac{-7}{18}=\frac{-16}{18}+\frac{-7}{18}=\frac{-23}{18}$;

$\frac{-25}{36}+\frac{-23}{18}=\frac{-25}{36}+\frac{-46}{36}=\frac{-71}{36}$.

Vậy ta điền được các phân số vào tháp số như sau:

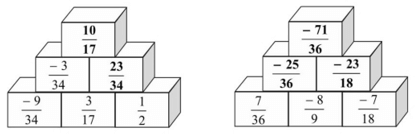
Xem thêm các bài giải SBT Toán 6 Cánh diều hay, chi tiết khác:

Bài 1: Phân số với tử và mẫu là số nguyên

Bài 2: So sánh các phân số. Hỗn số dương

Bài 4: Phép nhân, phép chia phân số

Bài 5: Số thập phân

Bài 6: Phép cộng, phép trừ số thập phân